State budgetary educational institution

Samara region secondary general education

school number 2 im. V. Maskina railway Art. Klyavlino

municipal district Klyavlinsky

Samara region

« Equations

and

inequalities

with parameters"

tutorial

Klyavlino

Tutorial

"Equations and inequalities with parameters" for students in grades 10-11

this manual is an appendix to the program elective course"Equations and Inequalities with Parameters", which has passed an external examination (by the scientific and methodological expert council of the Ministry of Education and Science of the Samara Region dated December 19, 2008, the ball is recommended for use in educational institutions Samara region)

Authors

Romadanova Irina Vladimirovna

Mathematics teacher, Klyavlinskaya Secondary General Education

school number 2 them. V. Maskina, Klyavlinsky district, Samara region

Serbaeva Irina Alekseevna

Introduction……………………………………………………………3-4

Linear equations and inequalities with parameters……………..4-7

Quadratic equations and inequalities with parameters……………7-9

Fractional rational equations with parameters……………..10-11

Irrational equations and inequalities with parameters……11-13

Trigonometric equations and inequalities with parameters.14-15

Exponential Equations and Inequalities with Parameters………16-17

Logarithmic equations and inequalities with parameters ...... 16-18

Tasks of the Unified State Examination………………………………………………………...18-20

Tasks for independent work…………………………...21-28

Introduction.

Equations and inequalities with parameters.

If in an equation or inequality some coefficients are not given by specific numerical values, but are indicated by letters, then they are called parameters, and the equation or inequality itself parametric.

In order to solve an equation or inequality with parameters, you must:

Highlight special meaning- this is the value of the parameter in which or when passing through which the solution of the equation or inequality changes.

Define allowed values are the parameter values ​​at which the equation or inequality makes sense.

Solving an equation or inequality with parameters means:

1) determine at what values ​​of the parameters solutions exist;

2) for each admissible system of parameter values, find the corresponding set of solutions.

An equation with a parameter can be solved by the following methods: analytical or graphical.

Analytical method assumes the task of investigating the equation by considering several cases, none of which can be missed.

The solution of the equation and inequality with parameters of each type by the analytical method involves a detailed analysis of the situation and a consistent study, during which the need arises "gentle handling" with a parameter.

Graphic method involves the construction of a graph of the equation, by which it is possible to determine how, respectively, the change in the parameter affects the solution of the equation. The graph sometimes allows one to analytically formulate the necessary and sufficient conditions for solving the set tasks. The graphical solution method is especially effective when it is necessary to establish how many roots the equation has depending on the parameter and has the undoubted advantage of seeing this visually.

§ 1. Linear equations and inequalities.

Linear Equation a x = b , recorded in general view, can be considered as an equation with parameters, where x – unknown , a , b - parameters. For this equation, the special or control value of the parameter is the one at which the coefficient vanishes in the unknown.

When solving a linear equation with a parameter, cases are considered when the parameter is equal to its special value and different from it.

Special parameter value a is the value a = 0.

b = 0 is a special parameter value b .

At b ¹ 0 the equation has no solutions.

At b = 0 the equation will take the form: 0x = 0. The solution to this equation is any real number.

Inequalities of the form ah > b and ax < b (a ≠ 0) are called linear inequalities. The set of solutions to the inequality ah >b– interval

(; +), if a > 0 , and (-;) , if a< 0 . Similarly for the inequality

Oh< b set of solutions - interval(-;), if a > 0, and (; +), if a< 0.

Example 1 solve the equation ax = 5

Solution: This is a linear equation.

If a = 0, then the equation 0 × x = 5 has no solution.

If a¹ 0, x =- solution of the equation.

Answer: at a¹ 0, x=

for a = 0 there is no solution.

Example 2 solve the equation ax - 6 \u003d 2a - 3x.

Solution: This is a linear equation ax - 6 \u003d 2a - 3x (1)

ax + 3x = 2a +6

Rewriting the equation as (a+3)x = 2(a+3) Let's consider two cases:

a= -3 and a¹ -3.

If a= -3, then any real number X is the root of equation (1). If a¹ -3 , equation (1) has a single root x = 2.

Answer: At a = -3, x R ; at a ¹ -3, x = 2.

Example 3 At what values ​​of the parameter a among the roots of the equation

2x - 4x - a 2 + 4а – 4 = 0 there are more roots 1 ?

Solution: Solve the equation 2x - 4x - a 2 + 4а – 4 = 0– linear equation

2 (a - 2) x \u003d a 2 - 4a +4

2(a - 2) x \u003d (a - 2) 2

At a = 2 solution of the equation 0x = 0 be any number, even greater than 1.

At a¹ 2 x =
. By condition x > 1, that is
>1, a > 4.

Answer: At a (2) U(4;∞).

Example 4 . For each parameter value a find the number of roots of the equation ax=8.

Solution. ax = 8 is a linear equation.

y = a– a family of horizontal lines;

y = - the graph is a hyperbola. We construct graphs of these functions.

Answer: If a = 0, then the equation has no solutions. If a ≠ 0, then the equation has one solution.

Example 5 . Using graphs, find out how many roots the equation has:

|x| = ax - 1.

y=| x | ,

y = ax - 1- the graph is a straight line passing through a point (0;-1).

We construct graphs of these functions.

Answer:When |a|>1- one root

at | a|≤1 The equation has no roots.

Example 6 . Solve the inequality ax + 4 > 2x + a 2

Solution : ax + 4 > 2x + a 2
(а – 2) х >a 2 – 4. Consider three cases.

Answer. x > a + 2 at a > 2; X<а + 2, at a< 2; at a=2 there are no solutions.

§ 2. Quadratic equations and inequalities

Quadratic equation is an equation of the form Oh ² + b x + c = 0 , where a≠ 0,

a, b , With - parameters.

To solve quadratic equations with a parameter, you can use the standard methods of solving using the following formulas:

1 ) discriminant of the quadratic equation: D = b ² - 4 ac , (
²- ac)

2) formulas of the roots of the quadratic equation:X 1 =
, X 2 =
,

(X 1,2 =
)

Square inequalities are called inequalities of the form

a X 2 + b x + c > 0,a X 2 + b x + c< 0, (1), (2)

a X 2 + b x + c ≥ 0,a X 2 + b x + c ≤ 0,(3), (4)

The set of solutions to inequality (3) is obtained by combining the sets of solutions to inequality (1) and the equation , a X 2 + b x + c=0. The set of solutions to inequality (4) is found similarly.

If the discriminant of a square trinomial a X 2 + b x + c less than zero, then for a > 0 the trinomial is positive for all x R.

If the square trinomial has roots (x 1 < х 2 ), then for a > 0 it is positive on the set(-; x 2 )
(X 2; +) and negative on the interval

(x 1; x 2 ). If a< 0, то трехчлен положителен на интервале (х one ; x 2 ) and is negative for all x (-; x 1 )
(X 2; +).

Example 1 solve the equation ax² - 2 (a - 1) x - 4 \u003d 0.

This is a quadratic equation

Solution: Special meaning a = 0.

At a = 0 we get a linear equation 2x - 4 = 0. It has a single root x = 2.

At a ≠ 0. Let's find the discriminant.

D \u003d (a-1)² + 4a \u003d (a + 1)²

If a = -1, then D = 0 - one root.

Find the root by substituting a = -1.

-x² + 4x - 4 \u003d 0, that is x² -4x + 4 = 0, we find that x=2.

If a ≠ - 1, then D >0 . According to the root formula, we get:x=
;

X 1 =2, x 2 = -.

Answer: At a=0 and a=-1 equation has one root x = 2; at a ≠ 0 and

a ≠ - 1 equation has two rootsX 1 =2, x 2 =-.

Example 2 Find the number of roots of the given equation x²-2x-8-a=0 depending on parameter values a.

Solution. Let us rewrite this equation in the form x²-2x-8=a

y \u003d x²-2x-8- the graph is a parabola;

y =a- a family of horizontal lines.

Let's build graphs of functions.

Answer: When a<-9 , the equation has no solutions; when a=-9, the equation has one solution; at a>-9, the equation has two solutions.

Example 3 At what a inequality (a - 3) x 2 – 2ax + 3a – 6 >0 holds for all values ​​of x?

Solution. The square trinomial is positive for all values ​​of x if

a-3 > 0 and D<0, т.е. при а, удовлетворяющих системе неравенств

, whence it follows thata > 6 .

Answer.a > 6

§ 3. Fractional-rational equations with a parameter,

reduced to linear

The process of solving fractional equations is carried out according to the usual scheme: the fractional is replaced by an integer by multiplying both parts of the equation by the common denominator of its left and right parts. After that, the whole equation is solved, excluding extraneous roots, that is, numbers that turn the denominator to zero.

In the case of equations with a parameter, this problem is more complicated. Here, in order to “eliminate” extraneous roots, it is required to find the value of the parameter that turns the common denominator to zero, that is, to solve the corresponding equations for the parameter.

Example 1 solve the equation
= 0

Solution: D.Z: x +2 ≠ 0, x ≠ -2

x - a \u003d 0, x \u003d a.

Answer: At a ≠ - 2, x=a

At a = -2 there are no roots.

Example 2 . solve the equation
-
=
(1)

This is a fractional rational equation

Solution: Meaning a = 0 is special. At a = 0 the equation loses its meaning and, therefore, has no roots. If a ≠ 0, then after transformations the equation will take the form: x² + 2 (1-a) x + a² - 2a - 3 = 0 (2)- quadratic equation.

Let's find the discriminant \u003d (1 - a)² - (a² - 2a - 3) \u003d 4, find the roots of the equationX 1 = a + 1, x 2 = a - 3.

When passing from equation (1) to equation (2), the domain of definition of equation (1) expanded, which could lead to the appearance of extraneous roots. Therefore, verification is necessary.

Examination. Exclude from found values X those in which

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.

If X 1 +1=0, that is (a+1) + 1= 0, then a = -2. In this way,

at a= -2 , X 1 -

If X 1 +2=0, that is (a+1)+2=0, then a = - 3. Thus, at a \u003d - 3, x 1 - extraneous root of the equation. (one).

If X 2 +1=0, that is (a - 3) + 1= 0, then a = 2. Thus, at a = 2 x 2 - extraneous root of equation (1).

If X 2 +2=0, that is ( a – 3) + 2 = 0, then a=1. Thus, at a = 1,

X 2 - extraneous root of equation (1).

In accordance with this, at a = - 3 we get x \u003d - 3 - 3 \u003d -6;

at a \u003d - 2 x \u003d -2 – 3= - 5;

at a \u003d 1 x \u003d 1 + 1 \u003d 2;

at a \u003d 2 x \u003d 2 + 1 \u003d 3.

You can write down the answer.

Answer: 1) if a= -3, then x= -6; 2) if a= -2, then x= -5; 3) if a=0, then there are no roots; 4) if a=1, then x=2; 5) if a=2, then x=3; 6) if a ≠ -3, a ≠ -2, a ≠ 0, a ≠ 1, a ≠ 2, then x 1 = a + 1, x 2 = a-3.

§4. Irrational equations and inequalities

Equations and inequalities in which the variable is contained under the root sign are called irrational.

The solution of irrational equations is reduced to the transition from an irrational to a rational equation by raising both sides of the equation to a power or by changing the variable. When both sides of the equation are raised to an even power, extraneous roots may appear. Therefore, when using this method, all found roots should be checked by substituting into the original equation, taking into account changes in the parameter values.

Type equation
=g (x ) is equivalent to the system

The inequality f (x) ≥ 0 follows from the equation f (x) = g 2 (x).

When solving irrational inequalities, we will use the following equivalent transformations:

≤ g(x)


≥g(x)

Example 1 Solve the Equation
= x + 1 (3)

This is an irrational equation

Solution: By definition of the arithmetic root, equation (3) is equivalent to the system
.

At a = 2 the first equation of the system has the form 0 x = 5, that is, it has no solutions.

At a≠ 2 x=
. Let us find out for what valuesa found valueX satisfies the inequalityx ≥ -1:
≥ - 1,
≥ 0,

where a ≤ or a > 2.

Answer: At a≤, a > 2 x=
, at < а ≤ 2 the equation has no solutions.

Example 2 solve the equation
= a (Annex 4)

Solution. y =

y = a is a family of horizontal lines.

Let's build graphs of functions.

Answer: at a<0 - there are no solutions

at a≥ 0 - one solution.

Example 3 . Let's solve the inequality(a+1)
<1.

Solution. O.D.Z. x ≤ 2. If a+1 ≤0, then the inequality holds for all admissible values X. If a+1>0, then

(a+1)
<1.

<

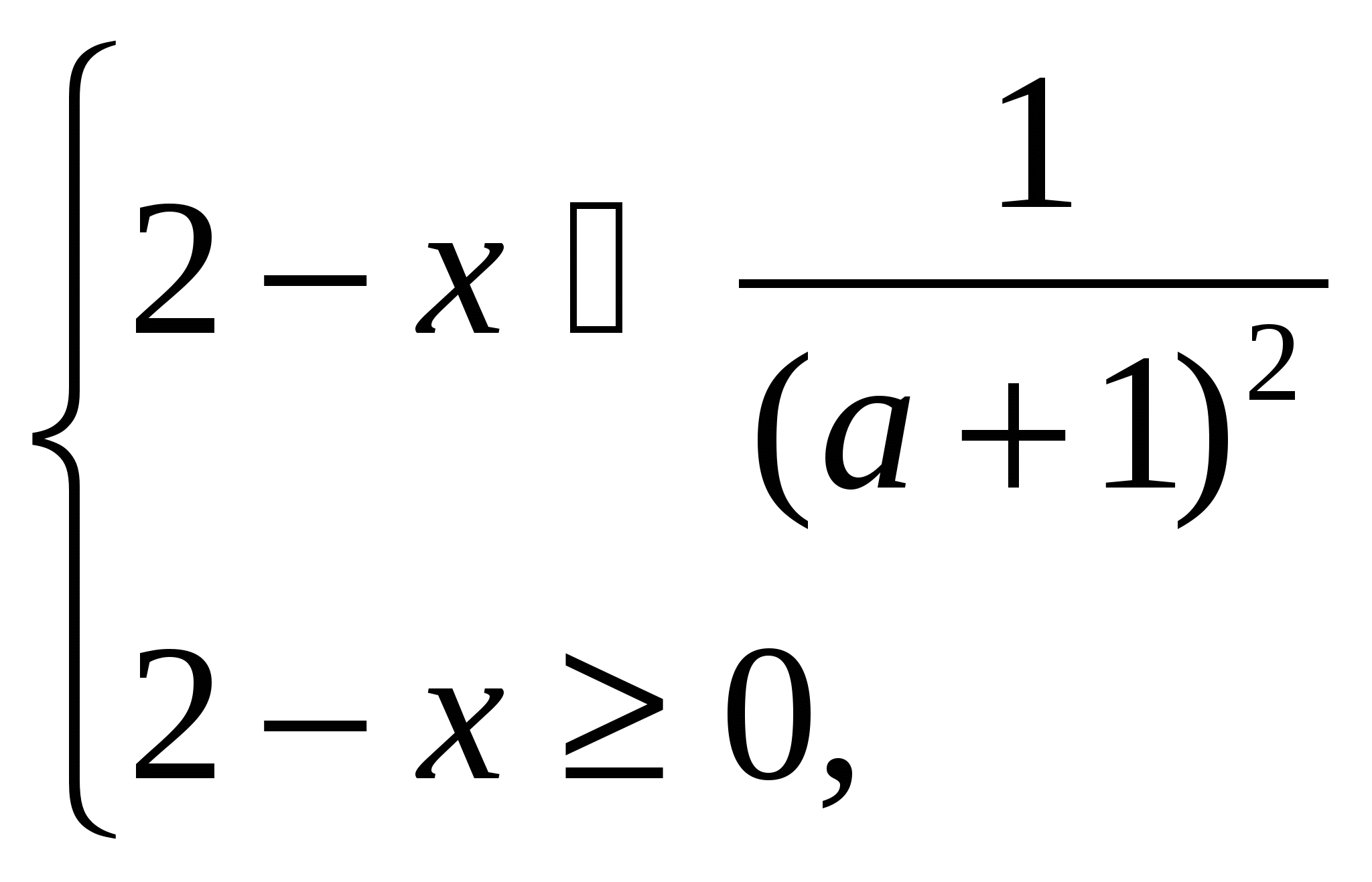
where X (2-
2

Answer. X (- ;2at a (-;-1, X (2-
2

at a (-1;+).

§ 5. Trigonometric equations and inequalities.

Here are the formulas for solving the simplest trigonometric equations:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ± arccos a + 2 πn, n Z, ≤1. (2)

If >1, then equations (1) and (2) have no solutions.

tan x = a
x= arctg a + πn, n Z, a R

ctg x = a
x = arcctg a + πn, n Z, a R

For each standard inequality, we indicate the set of solutions:

1. sin x > a
arcsin a + 2 n Z,

at a <-1, x R ; at a ≥ 1, there are no solutions.

2. . sin x< a
π - arcsin a + 2 πnZ,

for a≤-1, there are no solutions; when a>1,x R

3. cos x > a
- arccos a + 2 pn < x < arccos a + 2 pn , n Z ,

at a<-1, x R ; at a ≥ 1 , there are no solutions.

4. cos x arccos a+ 2 nZ,

at a≤-1 , there are no solutions; ata > 1, x R

5. tg x > a, arctg a + πnZ

6.tg x< a, -π/2 + πn Z

Example1. Find a, for which this equation has a solution:

Cos 2 x + 2(a-2) cosx + a 2 - 4a - 5 \u003d 0.

Solution. We write the equation in the form

Withos 2 x + (2 a -4) cosx +(a – 5)(а+1) =0, solving it as a square, we get cosx = 5-a and cosx = -a-1.

The equation cosx = 5- a has solutions provided -1≤ 5-a ≤1
4≤ a≤ 6, and the equation cosx = - a-1 provided -1≤ -1-a ≤ 1
-2 ≤ a ≤0.

Answer. a -2; 0
4; 6

Example 2 At what bthere exists a such that the inequality
+ b> 0 is satisfied for all x ≠pn , n Z .

Solution. Let's put a= 0. The inequality holds for b >0. Let us now show that no b ≤0 satisfies the conditions of the problem. Indeed, it suffices to put x = π /2, if a <0, и х = - π /2 at a ≥0.

Answer.b > 0

§ 6. Exponential equations and inequalities

1. Equation h(x) f ( x ) = h(x) g ( x) at h(x) > 0 is equivalent to the combination of two systems
and

2. In a particular case (h (x)= a ) the equation a f(x) = a g(x) at a> 0, is equivalent to the combination of two systems

and

3. Equation a f(x) = b , where a > 0, a ≠1, b>0, is equivalent to the equation

f(x)= log a b . Happening a=1 are considered separately.

Solution of the simplest exponential inequalities based on the degree property. Inequality of the formf(a x ) > 0 by changing the variablet= a x reduces to solving the system of inequalities
and then to the solution of the corresponding simplest exponential inequalities.

When solving a nonstrict inequality, it is necessary to add the roots of the corresponding equation to the set of solutions of a strict inequality. As with solving equations in all examples containing the expression a f (x ) , we assume a> 0. Case a= 1 are considered separately.

Example 1 . At what a equation 8 x =
has only positive roots?

Solution. By property exponential function with a base large units, we have x>0
8 X >1

>1

>0, whencea (1,5;4).

Answer. a (1,5;4).

Example 2 Solve the inequality a 2 ∙2 x > a

Solution. Consider three cases:

1. a< 0 . Since the left side of the inequality is positive and the right side is negative, the inequality holds for any x R.

2. a=0. There are no solutions.

3. a > 0 . a 2 ∙2 x > a
2 x >
x > -log 2 a

Answer. X R at a > 0; no solutions for a =0; X (- log 2 a; +) ata > 0 .

§ 7. Logarithmic equations and inequalities

Let us present some equivalences used in solving logarithmic equations and inequalities.

1. The equation log f (x) g (x) \u003d log f (x) h (x) is equivalent to the system

In particular, if a >0, a≠1, then

log a g(x)=log a h(x)

2. The equation log a g(x)=b
g(x)=a b ( a >0, a ≠ 1, g(x) >0).

3. Inequality log f ( x ) g (x) ≤ log f ( x ) h(x) is equivalent to the combination of two systems:
and

If a, b are numbers, a >0, a ≠1, then

log a f(x) ≤ b

log a f(x) > b

Example 1 Solve the Equation

Solution. Let's find ODZ: x > 0, x ≠ a 4 , a > 0, a≠ 1. Transform the equation

log x - 2 = 4 - log a x
log x + log a x– 6 = 0, whence log a x = - 3

x = a-3 and log a x = 2
x = a 2. Condition x = a 4
a – 3 = a 4 or a 2 = a 4 not performed on the ODZ.

Answer: x = a-3, x = a 2 at a (0; 1)
(1; ).

Example 2 . Find highest value a, for which the equation

2 log -
+ a = 0 has solutions.

Solution. Let's replace
= tand get the quadratic equation 2t 2 – t + a = 0. Solving, we findD = 1-8 a . Consider D≥0, 1-8 a ≥0
a ≤.

At a = quadratic equation has a roott= >0.

Answer. a =

Example 3 . Solve the inequalitylog(x 2 – 2 x + a ) > - 3

Solution. Let's solve the system of inequalities

Roots of square trinomials x 1,2 = 1 ±
their 3,4 = 1 ±
.

Critical parameter values: a= 1 and a= 9.

Let X 1 and X 2 be the solution sets of the first and second inequalities, then

X 1
X 2 = X is the solution to the original inequality.

At 0< a <1 Х 1 = (- ;1 -
)
(1 +
; +), ata> 1 x 1 = (-;+).

At 0< a < 9 Х 2 = (1 -
; 1 +
), ata≥9 Х 2 – no solutions.

Consider three cases:

1. 0< a ≤1 X = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a≥ 9 Х – no solutions.

USE tasks

High level C1, C2

Example 1 Find all values R, for which the equation

R ∙ ctg 2x+2sinx+ p= 3 has at least one root.

Solution. Let's transform the equation

R ∙ (
-1)+2sinx+ p\u003d 3, sinx \u003d t, t
, t 0.

- p+ 2t + p = 3, + 2t = 3, 3 -2t = , 3t2 – 2t3 = p .

Let f(y) = 3 t 2 – 2 t 3 . Let's find the set of function valuesf(x) on the


. at / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f(-1) = 5, f(1) = 1.

At t
, E(f) =
,

At t
, E(f) =
, that is, when t


, E(f) =
.

To Equation 3t 2 – 2 t 3 = p (hence the given) had at least one root necessary and sufficientp E(f), that is p
.

Answer.
.

Example 2

At what values ​​of the parametera the equation log
(4 x 2 – 4 a + a 2 +7) = 2 has exactly one root?

Solution. Let's transform the equation into an equivalent one:

4x 2 - 4 a + a 2 +7 \u003d (x 2 + 2) 2.

Note that if a certain number x is the root of the resulting equation, then the number - x is also the root of this equation. By condition, this is not feasible, so the only root is the number 0.

Let's find a.

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Examination.

1) a 1 = 1. Then the equation has the form:log
(4 x 2 +4) =2. We solve it

4x 2 + 4 \u003d (x 2 + 2) 2, 4x 2 + 4 \u003d x 4 + 4x 2 + 4, x 4 \u003d 0, x \u003d 0 is the only root.

2) a 2 = 3. The equation looks like:log
(4 x 2 +4) =2
x = 0 is the only root.

Answer. 1; 3

High level C4, C5

Example 3 Find all values R, under which the equation

x 2 - ( R+ 3)x + 1= 0 has integer roots and these roots are solutions to the inequality: x 3 - 7 R x 2 + 2x 2 - 14 R x - 3x +21 R ≤ 0.

Solution. Let x 1, X 2 are the integer roots of the equation x 2 – (R + 3)x + 1= 0. Then, by the Vieta formula, x 1 + x 2 = R + 3, x 1 ∙ x 2 = 1. The product of two integers x 1 , X 2 can be equal to one only in two cases: x 1 = x 2 = 1 or x 1 = x 2 = - 1. If x 1 = x 2 = 1, thenR + 3 = 1+1 = 2
R = - 1; if x 1 = x 2 = - 1, thenR + 3 = - 1 – 1 = - 2
R = - 5. Check whether the roots of the equation x 2 – (R + 3)x + 1= 0 in the cases described by the solutions of this inequality. For the occasionR = - 1, x 1 = x 2 = 1 we have

1 3 - 7 ∙ (- 1) ∙ 1 2 +2 ∙ 1 2 - 14 ∙ (- 1) ∙ 1 - 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 - true; for the occasion R\u003d - 5, x 1 \u003d x 2 \u003d - 1 we have (- 1) 3 - 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 - 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 is correct. So, the condition of the problem is satisfied only R= - 1 and R = - 5.

Answer.R 1 = - 1 and R 2 = - 5.

Example 4 Find all positive parameter values a, for which the number 1 belongs to the domain of the function

at = (a
- a
).

Course work

Artist: Bugrov S.K.

The study of many physical processes and geometric patterns often leads to the solution of problems with parameters. Some universities also include exam tickets equations, inequalities and their systems, which are often very complex and require a non-standard approach to solving. At school, this is one of the most difficult sections. school course Mathematics is considered only in a few elective classes.

Cooking this work, I set the goal of a deeper study of this topic, identifying the most rational solution that quickly leads to an answer. In my opinion, the graphical method is a convenient and fast way to solve equations and inequalities with parameters.

In my abstract, frequently encountered types of equations, inequalities and their systems are considered, and I hope that the knowledge I have gained in the process of work will help me when passing school exams and entering a university.

Inequality

¦(a, b, c, …, k, x)>j(a, b, c, …, k, x), (1)

where a, b, c, …, k are parameters and x is a real variable is called an inequality with one unknown containing the parameters.

Any system of parameter values ​​a = a0, b = b0, c = c0, …, k = k0, for some function

¦(a, b, c, …, k, x) and

j(a, b, c, …, k, x

make sense in the region of real numbers, is called the system of admissible parameter values.

is called a valid value of x if

¦(a, b, c, …, k, x) and

j(a, b, c, …, k, x

take real values ​​for any admissible system of parameter values.

The set of all admissible values ​​of x is called the domain of the inequality (1).

A real number x0 is called a particular solution of inequality (1) if the inequality

¦(a, b, c, …, k, x0)>j(a, b, c, …, k, x0)

is true for any system of admissible parameter values.

The set of all particular solutions of inequality (1) is called the general solution of this inequality.

To solve inequality (1) means to indicate for what values ​​of the parameters there is a general solution and what it is.

Two inequalities

¦(a, b, c, …, k, x)>j(a, b, c, …, k, x) and (1)

z(a, b, c, …, k, x)>y(a, b, c, …, k, x) (2)

are called equivalent if they have the same general solutions for the same set of systems of admissible parameter values.

Find the domain of definition of this inequality.

We reduce the inequality to an equation.

We express a as a function of x.

In the xOa coordinate system, we construct graphs of the functions a =¦ (x) for those values ​​of x that are included in the domain of definition of this inequality.

We find sets of points that satisfy this inequality.

We investigate the influence of the parameter on the result.

find the abscissas of the intersection points of the graphs.

set the line a=const and shift it from -¥ to +¥

We write down the answer.

This is just one of the algorithms for solving inequalities with parameters using the x0a coordinate system. Other methods of solution are also possible, using the standard xOy coordinate system.

§3. Examples

I. For all admissible values ​​of the parameter a, solve the inequality

In the domain of the parameter a defined by the system of inequalities

this inequality is equivalent to the system of inequalities

If , then the solutions of the original inequality fill the segment .

II. For what values ​​of the parameter a does the system have a solution

Find the roots of the trinomial on the left side of the inequality -

(*)

The straight lines given by the equalities (*) divide the a0x coordinate plane into four regions, each of which contains a square trinomial

retains a constant sign. Equation (2) defines a circle of radius 2 centered at the origin. Then the solution to the original system will be the intersection shaded

a circle with a circle, where , and the values ​​and are found from the system

and the values ​​and are found from the system

Solving these systems, we get that

III. Solve the inequality on depending on the values ​​of the parameter a.

We find the area of ​​​​admissible values ​​-

Let's build a graph of the function in the xOy coordinate system.

when the inequality has no solutions.

when for solution x satisfies the relation , where

Answer: Solutions to the inequality exist for

Where , and when solving ; when solving.

IV. Solve the inequality

Finding ODZ or discontinuity lines (asymptotes)

Let's find the equations of functions, the graphs of which need to be plotted in the UCS; for which we turn to equality:

Let's factorize the numerator.

because then

Let us divide both parts of the equality by at . But it is a solution: the left side of the equation is equal to the right side and is equal to zero at .

3. We build graphs of functions in PSC xOa

and number the resulting regions (the axes do not play a role). There were nine regions.

4. We are looking for which of the regions is suitable for this inequality, for which we take a point from the region and substitute it into the inequality.

For clarity, let's make a table.

		inequality:

5. Find the intersection points of the graphs

6. Let's set a straight line a=const and we will shift it from -¥ to +¥.

at

with no solutions

at

Bibliography

Dalinger V. A. “Geometry Helps Algebra”. Publishing house "School - Press". Moscow 1996

Dalinger V. A. “Everything to ensure success at graduation and entrance exams mathematics". Publishing house of the Omsk Pedagogical University. Omsk 1995

Okunev A. A. “ Graphic solution equations with parameters”. Publishing house "School - Press". Moscow 1986

Pismensky D. T. “Mathematics for high school students”. Iris Publishing House. Moscow 1996

Yastribinetskiy G. A. “Equations and inequalities containing parameters”. Publishing house "Enlightenment". Moscow 1972

G. Korn and T. Korn “Handbook of Mathematics”. Publishing house "Nauka" physical and mathematical literature. Moscow 1977

Amelkin V. V. and Rabtsevich V. L. “Problems with parameters” . Publishing house "Asar". Moscow 1996

Elective course lesson

on this topic: "Solving Equations and Inequalities with Parameters"

(Lesson of generalization and repetition)

Target: 1. Repeat and generalize students' knowledge of methods for solving equations and inequalities with parameters; to consolidate the ability to apply knowledge in solving specific tasks; 2. Develop logical thinking; 3. To cultivate attention and accuracy.

Lesson plan: I. Organizational moment _____________________________ 2 min.

II. Updating of basic knowledge:

1. Revision __________________________________ 3 min.
2. Oral work________________________________3 min.
3. Card work (during 1 and 2)

III. Solution of exercises _____________________ 22 min.

I.Y. Performing the test ____________________________ 8 min.

Y. Summing up, setting homework__2 min.

During the classes:

I. Organizing time.

Teacher: - Hello guys. It's nice to see you all, we're starting our lesson. Today in the lesson, our goal is to repeat and work out the knowledge, skills and abilities gained in previous lessons while studying this topic.

II . Updating of basic knowledge:

1) Repetition.

Teacher: So let's repeat.

What is called a linear equation with parameters?

What cases did we consider when solving such equations?

Give examples linear equations with parameters.

Give examples linear inequalities with parameters.

2) Oral work.

Task: Bring this equation to a linear form.

On the desk:

a) 3a x - 1 \u003d 2 x;

b) 2+5 x \u003d 5a x;

c) 2 x - 4 \u003d a x + 1.

3) Work on cards.

III . Solution of exercises.

Exercise 1. Solve an equation with a parameter a.

3(ax + 1) + 1 = 2(a - x) + 1.

The assignment is done on the board and in notebooks.

Task 2. At what value a, straight line y \u003d 7ax + 9, passes through

t. A(-3;2) ?

The task is performed independently at the blackboard by one student. The rest work in notebooks, then check with the board.

Fizkult. minute.

Task 3. At what value a, the equation 3(ax - a) = x - 1 has

Infinitely many solutions?

This task is proposed to be solved independently by students in notebooks. Then check the answers.

Task 4. At what value of the parameter a , the sum of the roots of the equation

2x² + (4a² - 2)x - (a² + 1) = 0 equal to 1?

The task is performed by commenting from the spot.

Task 5. Solve Inequality with Parameter R :

p(5x - 2)

This task is carried out at the blackboard and in notebooks.

I.Y. Test execution.

Students are given individual worksheets with tasks:

1) Is the equation6(ax + 1) + a = 3(a - x) + 7 linear?

A) yes; b) no; c) can be reduced to a linear

2) Equation (2ax + 1) a = 5a - 1 reduced to the form of a linear equation

A) no; b) yes;

3) At what value of the parameter and the straight line y \u003d ax - 3 passes through

T. A(-2;9) ?

A) a \u003d 1/6; b) a = 1/2; c) a = -6; d) a = 6.

4) At what a equation 2ax + 1 = x has a root equal to -1?

a) a = -1; b) a = 0; c) a = 1; d) a = 1/2.

5) If the quadratic equation ax² + in + c \u003d 0 D ax² + in + c >0 depends on

A) values ​​in; b) values ​​a; c) values ​​\u200b\u200b-v / a;

d) has no solutions.

Answers to the test: v; a; v; v; b.

YII. Summing up the lesson. Setting homework.

Teacher: - Today at the lesson we repeated and consolidated the knowledge gained in previous lessons, worked out the necessary skills when performing various tasks. I think you did a good job, well done.

In addition to the marks given for the lesson, it is possible to evaluate the work of a number of other students in the lesson.

Teacher : - Write down your homework:

On the desk:

Solve the inequality: x² - 2ax + 4 > 0.

The lesson is over.

A person who knows how to solve problems with parameters knows the theory perfectly and knows how to apply it not mechanically, but with logic. He "understands" the function, "feels" it, considers it his friend or at least a good acquaintance, and not just knows about its existence.

What is an equation with a parameter? Let the equation f (x; a) = 0 be given. If the task is to find all such pairs (x; a) that satisfy this equation, then it is considered as an equation with two equal variables x and a. But it is possible to pose another problem, assuming that the variables are unequal. The fact is that if you give the variable a some fixed value, then f (x; a) \u003d 0 turns into an equation with one variable x, and the solutions to this equation naturally depend on the chosen value of a.

The main difficulty associated with solving equations (and even more so inequalities) with a parameter is as follows: - for some values ​​of the parameter, the equation has no solutions; -for others, it has infinitely many solutions; - with the third - it is solved by one formula; - at the fourth - it is solved by other formulas. - If the equation f (x; a) = 0 needs to be solved with respect to the variable X, and a is understood as an arbitrary real number, then the equation is called an equation with the parameter a.

To solve an equation with the parameter f (x; a) = 0 is to solve a family of equations resulting from the equation f (x; a) = 0 for any real values ​​of the parameter. An equation with a parameter is, in fact, a shorthand for an infinite family of equations. Each of the equations of the family is obtained from the given equation with a parameter at a specific value of the parameter. Therefore, the problem of solving an equation with a parameter can be formulated as follows:

It is impossible to write down every equation from an infinite family of equations, but nevertheless, every equation from an infinite family must be solved. This can be done, for example, if, according to some reasonable criterion, the set of all values ​​of the parameter is divided into subsets, and then the given equation is solved on each of these subsets. Solving linear equations

To divide the set of parameter values ​​into subsets, it is useful to use those parameter values ​​at which or when passing through which a qualitative change in the equation occurs. Such parameter values ​​can be called control or special. The art of solving an equation with parameters is precisely to be able to find the control values ​​of the parameter.

Type 1. Equations, inequalities, their systems, which must be solved either for any parameter value, or for parameter values ​​that belong to a predetermined set. This type of problem is basic when mastering the topic "Problems with parameters", since the invested work predetermines success in solving problems of all other basic types.

Type 2. Equations, inequalities, their systems, for which it is required to determine the number of solutions depending on the value of the parameter (parameters). When solving problems of this type, there is no need to either solve the given equations, inequalities, their systems, or give these solutions; such extra work in most cases is a tactical mistake, leading to unjustified expenditure of time. But sometimes a direct solution is the only reasonable way to get an answer when solving a type 2 problem.

Type 3. Equations, inequalities, their systems, for which it is required to find all those values ​​of the parameter for which the specified equations, inequalities, their systems have a given number of solutions (in particular, they do not have or have an infinite number of solutions). Problems of type 3 are in some sense the inverse of problems of type 2.

Type 4. Equations, inequalities, their systems and collections, for which, for the desired values ​​of the parameter, the set of solutions satisfies the given conditions in the domain of definition. For example, find the values ​​of the parameter for which: 1) the equation is satisfied for any value of the variable from a given interval; 2) the set of solutions of the first equation is a subset of the set of solutions of the second equation, and so on.

The main ways (methods) of solving problems with a parameter. Method I (analytical). The analytical method of solving problems with a parameter is the most difficult method, requiring high literacy and the greatest effort to master it. Method II (graphic). Depending on the task (with variable x and parameter a), graphs are considered or in coordinate plane Oxu, or in the Oxa coordinate plane. Method III (parameter decision). When solving in this way, the variables x and a are taken equal, and the variable is chosen, with respect to which the analytical solution is recognized as simpler. After natural simplifications, we return to the original meaning of the variables x and a and complete the solution.

Example 1. Find the values ​​of the parameter a for which the equation a (2a + 3)x + a 2 = a 2 x + 3a has a single negative root. Solution. This equation is equivalent to the following:. If a (a + 3) 0, that is, a 0, a -3, then the equation has a single root x =. X

Example 2. Solve the equation. Solution. Since the denominator of a fraction cannot be equal to zero, we have (b - 1) (x + 3) 0, that is, b 1, x -3. Multiplying both sides of the equation by (b - 1)(x + 3) 0, we get the equation: This equation is linear in x. For 4b - 9 = 0, that is, b = 2.25, the equation becomes: For 4b - 9 0, that is, b 2.25, the root of the equation is x =. Now we need to check if there are such values ​​of b for which the found value of x is equal to -3. Thus, for b 1, b 2.25, b -0.4, the equation has a single root x =. Answer: at b 1, b 2.25, b –0.4 root x = at b = 2.25, b = –0.4 there are no solutions; for b = 1, the equation is meaningless.

Types of problems 2 and 3 are distinguished by the fact that when solving them, it is not required to obtain an explicit solution, but it is only necessary to find those values ​​of the parameter for which this solution satisfies certain conditions. Examples of such conditions for a solution are the following: there is a solution; there is no solution; there is only one solution; there is a positive solution; there are exactly k solutions; there exists a solution that belongs to the indicated interval. In these cases it is very useful. graphic way solving problems with parameters.

There are two types of application of the graphical method in solving the equation f (x) = f (a): On the Oxy plane, a graph y \u003d f (x) and a family of graphs y \u003d f (a) are considered. This also includes problems solved with the help of a "bundle of lines". This method turns out to be convenient in problems with two unknowns and one parameter. On the Ox plane (which is also called the phase plane), graphs are considered in which x is the argument, and a is the value of the function. This method is usually used in problems in which only one unknown and one parameter appear (or are reduced to such).

Example 1. For what values ​​of the parameter a does the equation 3x 4 + 4x 3 - 12x 2 = a have at least three roots? Solution. Let's plot the graphs of the functions f (x) \u003d 3x 4 + 4x 3 - 12x 2 and f (x) \u003d a in one coordinate system. We have: f "(x) \u003d 12x x 2 - 24x \u003d 12x (x + 2) (x - 1), f "(x) \u003d 0 at x \u003d -2 (minimum point), at x \u003d 0 (maximum point ) and at x = 1 (maximum point). Let's find the function values ​​at the extremum points: f (–2) = –32, f (0) = 0, f (1) = –5. We build a schematic graph of the function, taking into account the extremum points. The graphical model allows you to answer the question: the equation 3x 4 + 4x 3 - 12x 2 = a has at least three roots, if -5

Example 2. How many roots does the equation have for different values ​​of the parameter a? Solution. The answer to the question posed is related to the number of points of intersection of the graph of the semicircle y \u003d and the straight line y \u003d x + a. A straight line that is tangent has the formula y = x +. Given Equation has no roots at a; has one root at -2

Example3. How many solutions does the equation |x + 2| = ax + 1 depending on the parameter a? Solution. You can plot y = |x + 2| and y = ax + 1. But we will do otherwise. For x = 0 (21) there are no solutions. Divide the equation by x: and consider two cases: 1) x > -2 or x \u003d 2 2) 2) x -2 or x \u003d 2 2) 2) x

An example of using a "pencil of lines" on a plane. Find the values ​​of the parameter a for which the equation |3x + 3| = ax + 5 has a unique solution. Solution. Equation |3x + 3| = ax + 5 is equivalent to the following system: The equation y – 5 = a(x – 0) defines a pencil of lines on the plane with center A (0; 5). Let's draw lines from a pencil of lines that will be parallel to the sides of the corner, which is the graph y = |3x + 3|. These lines l and l 1 intersect the graph y = |3x + 3| at one point. The equations of these lines are y = 3x + 5 and y = –3x + 5. In addition, any line from the pencil located between these lines will also intersect the graph y = |3x + 3| at one point. Hence, the desired values ​​of the parameter [–3; 3].

Algorithm for solving equations using the phase plane: 1. Find the domain of the equation. 2. We express the parameter a as a function of x. 3. In the xOa coordinate system, we plot the function a = f(x) for those values ​​of x that are included in the domain of definition of this equation. 4. We find the points of intersection of the straight line a \u003d c, where c є (-; +) with the graph of the function a \u003d f (x). If the straight line a \u003d c intersects the graph a \u003d f (x), then we determine the abscissas of the intersection points. To do this, it is enough to solve the equation a \u003d f (x) with respect to x. 5. We write down the answer.

An example of solving an inequality using the "phase plane". Solve the x inequality. Solution. By equivalent transition Now, on the Ox plane, we construct graphs of functions. The points of intersection of the parabola and the straight line x 2 - 2x \u003d -2x x \u003d 0. The condition a -2x is automatically satisfied for a x 2 - 2x Thus, in the left half-plane (x

Municipal Autonomous Educational Institution "Lyceum No. 1", Novotroitsk

Research

Methods for solving equations and inequalities with a parameter

Mathematical modeling

Completed:

student 11 A grade MOAU

"Lyceum №1"

Supervisor:

higher education teacher

Novotroitsk

Introduction. 3

Parameter. 5

Methods for solving trigonometric equations with a parameter. 9

Methods for solving exponential and logarithmic equations and inequalities with a parameter. 17

Methods for solving systems of equations and inequalities. 22

Conclusion. 31

List of used literature.. 32

Introduction

Equations with a parameter call great difficulty for students in grades 9-11. This is due to the fact that the solution of such equations requires not only knowledge of the properties of functions and equations, the ability to perform algebraic transformations, but also a high logical culture and research technique.

Difficulties when studying this type of equations, they are associated with the following features:

an abundance of formulas and methods used in solving equations of this type;

the possibility of solving the same equation containing a parameter in different ways.

Relevance the topic is due to the insufficient content of tasks on this topic in the textbook "Algebra Grade 11".

The importance of this topic is determined by the need to be able to solve such equations with parameters as in the case of passing the Unified state exam as well as entrance examinations to higher educational institutions.

Object of study: tasks with parameters.

The purpose of this work:

Reveal, substantiate and visually show ways to solve all types of equations with parameters;

Solve equations with parameters;

Deepen theoretical knowledge on solving equations with parameters;

To achieve this goal, it is necessary to solve the following tasks:

1. Define the concepts of an equation with parameters;

2. Show ways to solve equations with parameters.

The merit of my work consists in the following: algorithms for solving equations with parameters are indicated; problems are often found in various exams and olympiads. The work will help students pass the Unified State Exam.

My actions:

1. Pick up and study literature;

2. Solve selected tasks;

Parameter

There are several definitions parameter:

- Parameter - this is a quantity included in formulas and expressions, the value of which is constant within the problem under consideration, but in another problem it changes its values ​​(, - " Dictionary mathematical terms).

- Variables a, b, c, …, k, which are considered constant when solving an equation or inequality, are called parameters, and the equation itself (inequality) is called an equation (inequality) containing parameters (- "Tutor in Mathematics", Rostov-on-Don "Phoenix" 1997).

The solution of most equations containing a parameter reduces to quadratic equations with parameter. Therefore, in order to learn how to solve exponential, logarithmic, trigonometric equations and systems of equations with a parameter, you must first acquire the skills of solving quadratic equations with parameter.

Type equation ax2 + bx+ c=0 , where x is an unknown, a, b, c are expressions depending only on parameters, a¹0, is called quadratic equation regarding x. We will consider only those values ​​of parameters for which a, b, c are valid.

Parameter Control Values

To solve quadratic equations with a parameter, it is necessary to find parameter control values.

Parameter Control Values- those values ​​at which it turns to 0:

The leading coefficient in an equation or inequality;

Denominators in fractions;

The discriminant of a square binomial.

General scheme for solving equations reducible to quadratic equations with a parameter.

The general scheme for solving equations reduced to quadratic equations with a parameter:

1. Indicate and exclude all values ​​of the parameter and variable for which the equation loses its meaning.

2. Multiply both sides of the equation by a common denominator that is not zero.

3. Convert the consequence equation to the form https://pandia.ru/text/80/147/images/image002_13.png" width="128" height="24 src="> - real numbers or functions of the parameter.

4. Solve the resulting equation by considering the cases:

a) ; b) https://pandia.ru/text/80/147/images/image005_6.png" width="19" height="27">.png" width="21" height="27">.png" height="75">x=2b+1

Since x must lie between 1 and 6, then:
1) 1<2b+1<6

2) 1<2b – 1<6

https://pandia.ru/text/80/147/images/image009_4.png" width="47" height="41 src=">=2b+1

1) 1<2b+1<6

2) 1<2b – 1<6

https://pandia.ru/text/80/147/images/image010_2.png" width="18 height=98" height="98">

y(1)>0 y=1-4b+4b2– 1>0

y(6)> 0 y=36-24b+4b2– 1>0

хвн(1; 6) 1<-<6

bн(-∞; 0) È (1; +∞).

2) 4b2-24b+35>0

D=576 – 560=16=42>0

b1=https://pandia.ru/text/80/147/images/image016_2.png" width="47" height="41 src=">=2.5 bÎ(0.5; 3)

bн(-∞;2,5)И(3,5;+∞)
bн(1; 2,5)

Answer: the roots of the equation x2-4bx+4b2–1=0 lie on the interval from