Wave properties of particles. Download the book "General and Inorganic Chemistry" (5.36Mb) Which of the following particles have wave properties

28.03.2020

Quantum mechanics is a modern theory that establishes the method of description and the laws of motion of microparticles ( elementary particles, atoms, molecules, nuclei) and their systems. The unusualness of quantum mechanical concepts in comparison with classical physics opened a period of breaking the basic physical models, which seemed obvious and indestructible. This mainly concerned the concept of a particle and the principles of its motion.

This chapter gives a concept not only about quantum mechanics, but also about those ideas and experiments that led to this theory. Electron microscopy is considered as a method based on the wave properties of electrons.

28.1. DE BROYLE'S HYPOTHESIS. EXPERIMENTS ON THE DIFFRACTION OF ELECTRONS AND OTHER PARTICLES

An important step in the creation of quantum mechanics was the discovery of the wave properties of microparticles. The idea of wave properties was originally put forward as a hypothesis by the French physicist Louis de Broglie (1924) 1 .

In physics for many years the theory dominated, according to which light is an electromagnetic wave. However, after the work of Planck (thermal radiation), Einstein (photoelectric effect) and others, it became obvious that light has corpuscular properties.

1 De Broglie's hypothesis was formulated before experiments confirming the wave properties of particles. De Broglie wrote about this later, in 1936, as follows: “... can we not assume that the electron is as dual as light? At first glance, this idea seemed very daring. After all, we have always imagined an electron as an electrically charged material point, which obeys the laws of classical dynamics. The electron has never explicitly exhibited wave properties such as, say, light exhibits in the phenomena of interference and diffraction. Attempting to attribute wave properties to an electron, when there is no experimental evidence for this, could look like an unscientific fantasy.”

In ch. 24 it was noted that X-ray diffraction is observed on crystalline bodies; therefore, crystalline substances must also be used for electron diffraction.

K. Davisson and L. Germer were the first to observe electron diffraction on a single crystal of nickel, J.P. Thomson and, independently of him, P.S. Tartakovsky - on a metal foil (a polycrystalline body).

On fig. 28.1 shows an electron gram - a diffraction pattern obtained from the interaction of electrons with a polycrystalline foil.

Comparing this figure with Fig. 24.21, one can notice the similarity of electron and x-ray diffraction.

Other particles also have the ability to diffract, both charged (protons, ions, etc.) and neutral (neutrons, atoms, molecules).

Similar to X-ray diffraction analysis, particle diffraction can be used to determine the ordered or disordered arrangement of atoms and molecules of a substance and to estimate the parameters of crystal lattices.

At present, electron diffraction (electron diffraction) and neutron diffraction (neutron diffraction) methods are widely used.

Questions may arise: what happens to individual particles, how are the maxima and minima formed during the diffraction of individual particles?

Experiments on the diffraction of electron beams of very low intensity, i.e. as if separate particles, showed that in this case the electron is not "smeared" in different directions, but behaves like a whole particle. However, the probability of electron deflection in separate directions as a result of interaction with the diffraction object is different. The electrons are most likely to hit the places that, according to the calculation, correspond to the diffraction maxima, their hit to the minima is less likely. Thus, wave properties are inherent not only to the collective of electrons, but also to each electron individually.

28.2. ELECTRON MICROSCOPE. THE CONCEPT OF ELECTRONIC OPTICS

The wave properties of particles can be used not only for diffraction structural analysis, but also for obtaining enlarged images of an object.

From (26.19) it follows that the resolution limit of an optical microscope is mainly determined by the limiting value of the wavelength of light perceived by the human eye. Substituting in this formula the value of the de Broglie wavelength (28.3), we find the resolution limit of the electron microscope, in which the image of the object is formed by electron beams:

It is easy to see that the resolution limit z electron microscope depends on the accelerating voltage, and it can be achieved that it is much smaller, and the resolution is much greater than that of an optical microscope.

An electron microscope and its individual elements are similar in purpose to an optical one, so we will use an analogy to explain its structure and principle of operation. The diagrams of both microscopes are shown in fig. 28.2 (a - optical; b - electronic).

In an optical microscope, the carrier of information about the subject AB is a photon, light. The light source is usually an incandescent lamp /. After interaction with the object (absorption, scattering, diffraction), the photon flux is transformed and contains information about the object. The photon flux is formed using optical devices, mainly lenses: condenser 3, objective 4, eyepiece 5. Image A 1 B 1 is recorded by eye 7 (or a photographic plate, photoluminescent screen, etc.).

In an electron microscope, the carrier of information about an object is an electron, and the source of electrons is a heated cathode 1. The acceleration of electrons and the formation of a beam is carried out by a focusing electrode and an anode - a system called an electron gun 2. After interacting with the object (mainly scattering), the electron flow is converted and contains information about the subject. The formation of an electron flow occurs under the influence of an electric field (a system of electrodes and capacitors) and a magnetic field (a system

ma coils with current). These systems are called electronic lenses by analogy with optical lenses that form a light flux. (3 - condenser; 4 - electronic, serving as a lens, 5 - projection). The image is recorded on an electron-sensitive photographic plate or cathodoluminescent screen 6.

To estimate the resolution limit of an electron microscope, let us substitute into formula (28.4) an accelerating voltage of 100 kV and an angular aperture of the order of 10 -2 rad (approximately such angles are used in electron microscopy). Then we get z ~ 0.1 nm, which is hundreds of times better than optical microscopes. The use of an accelerating voltage greater than 100 kV, although it increases the resolution, is associated with some difficulties, in particular, it occurs

destruction of the object under study by electrons having a high speed. In practice, even with the best electron microscope, a resolution limit of the order of 10 -10 m can be achieved; this is hundreds of times better than optical microscopes.

The advantages of an electron microscope include a large resolution that allows one to consider large molecules, the ability to change, if necessary, the accelerating voltage and, consequently, the resolution limit, and relatively convenient control of the electron flow using magnetic and electric fields.

Let us indicate some features of the operation of an electron microscope. In those parts of it where electrons fly, there must be a vacuum, since otherwise the collision of electrons with air (gas) molecules will distort the image. This requirement for electron microscopy complicates the examination procedure, makes the equipment more cumbersome and expensive. Vacuum distorts the native properties of biological objects, and in some cases destroys or deforms them.

Only very thin sections are suitable for viewing in an electron microscope, since electrons are strongly absorbed and scattered by the substance. Therefore, in some cases it is advisable to make an imprint of the investigated surface of the object on a thin layer of plastic. This procedure is called replication, and a plastic copy of the surface is replica.

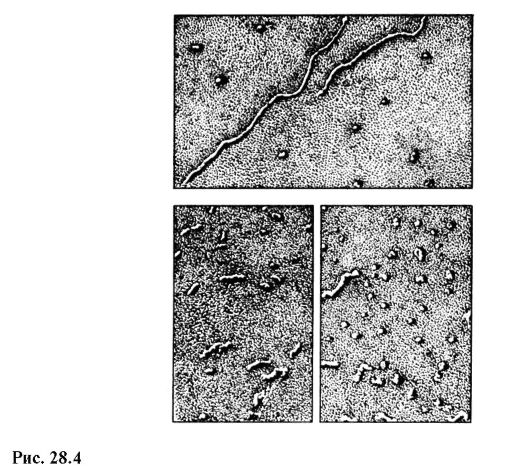
The modern domestic electronic microscope EVM-100 LM (Fig. 28.3) gives a maximum magnification of 600,000 times and a guaranteed resolution limit of 3? 10 -10 m. In fig. 28.4 shows pictures of RNA molecules in different states, obtained on an electron microscope with a magnification of 100,000 times.

The presence of wave and corpuscular properties of both photons and electrons and other particles allows a number of provisions and laws of optics to be extended to describe the motion of charged particles in electric and magnetic fields.

This analogy made it possible to single out as an independent section electronic optics - a field of physics in which the structure of beams of charged particles interacting with electrical and magnetic fields. Like conventional optics, electronic can be divided into geometric (beam) and wave(physical).

Within the framework of geometric electron optics, in particular, the motion of charged particles in electric and magnetic fields is described. The schematic representation of imaging in an electron microscope (see Fig. 28.2, b) is based on geometric electron optics.

The approach of wave electron optics is essential in the case when the wave properties of charged particles are manifested. A good illustration is finding the resolution (resolution limit) given at the beginning of the paragraph.

28.3. WAVE FUNCTION AND ITS PHYSICAL MEANING

Since a microparticle is associated with a wave process that corresponds to its motion, the state of particles in quantum mechanics is described by a wave function that depends on coordinates and time: ψ(χ, y, z, t).

If the force field acting on the particle is stationary, i.e. independent of time, then the ψ-function can be represented as a product of two factors, one of which depends on time, and the other on coordinates:

In what follows, we will consider only stationary states; The ψ-function is a probabilistic characteristic of the state of a particle. Let us explain the meaning of this statement.

Let us allocate a sufficiently small volume in space dV= dxdjdz, within which the values of the ψ-function can be considered the same. Probability of finding dW B particles in this volume is proportional to the volume and depends on the square of the modulus of the ψ-function:

The square of the modulus of the wave function is equal to the probability density, i.e. the ratio of the probability of finding a particle in a volume to this volume.

Integrating expression (28.6) over some volume V, we find the probability of finding a particle in this volume:

28.4. UNCERTAINTY RELATIONS

One of the important provisions of quantum mechanics are the uncertainty relations proposed by W. Heisenberg.

Let the position and momentum of the particle be measured simultaneously, while the inaccuracies in the definitions of the abscissa and the projection of the momentum on the abscissa axis are Δχ and Δр x, respectively.

1 Really it is impossible to carry out such an experiment, since the dimensions of the gap must be of the order of atoms, therefore, some mental experiment is described.

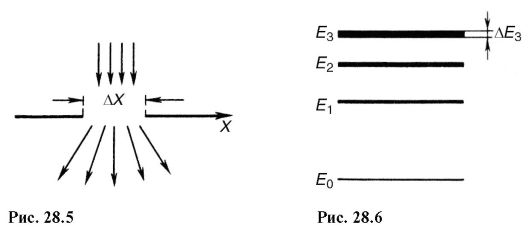
The solution (28.11) means that the shorter the time of existence of any state of the system, the more uncertain its value of energy. Energy levels E 1 , E 2 etc. have a certain width (Fig. 28.6), depending on the time the system is in the state corresponding to this level.

The “blurring” of the levels leads to the uncertainty of the energy AE of the emitted photon and its frequency Ay during the transition of the system from one energy level to another:

Since the state of a microparticle is described by the ψ-function, it is necessary to indicate the method for finding this function, taking into account external conditions. This is possible as a result of solving the basic equation of quantum mechanics proposed by E. Schrödinger (1926). Such an equation in quantum mechanics is postulated in the same way as in classical mechanics Newton's second law is postulated.

As applied to stationary states, the Schrödinger equation can be written as follows:

This manifests itself in the broadening of the spectral lines.

28.5. SCHROEDINGER EQUATION. ELECTRON IN A POTENTIAL WELL

where m- particle mass; E and E p are its total and potential energies (the potential energy is determined by the force field in which the particle is located, and for the stationary case does not depend on time).

If the particle moves only along some line, for example along the axis X(one-dimensional case), then the Schrödinger equation is significantly simplified and takes the form:

One of the most simple examples on the use of the Schrödinger equation is the solution of the problem of the motion of a particle in a one-dimensional potential well.

Let the electron move along the axis X only within 0< X < l(Fig. 28.7). This means that in the indicated interval the ψ-function is nonzero, and outside the interval (x<0, X>l) is equal to zero.

Since the force fields do not act on the particle in the selected interval, its potential energy can have any constant value (it is most convenient to take E p= 0). Outside this interval, there is no electron, so its potential energy should be considered infinitely large. On fig. 28.7 shows a graphical dependence of E p \u003d D x). Interval 0< X < l, удовлетворяющий сформулированным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом E p= 0 Schrödinger equation (28.14) for interval 0< X < l looks like:

This equation is similar differential equation harmonic oscillation (see 7.1) whose solution is:

First of all, it is noteworthy that the solution of the Schrödinger equation for an electron in a potential well without any additional postulates leads to discrete, quantized energy values:

From (28.21) it can be seen that for some fixed value n discreteness, i.e. the difference in the energies of neighboring levels is the smaller, the larger the size of the potential well. For example, consider two cases n = 1:

1) l= 5? 10 -10 m, which roughly corresponds to the size of an atom; then ΔΕ = 4.5 eV. This coincides in order of magnitude with the values obtained for the hydrogen atom according to Bohr's theory;

2) l= 10 -1 m, which actually corresponds to such a width of the potential well that the electron can be considered free; wherein ΔΕ = 1.1? 10 -16 eV. Here, the discreteness is negligible and practically it can be considered that the electron energy changes continuously.

Squaring (28.20), we get the probability density |ψ| 2 finding an electron in different points potential hole. On fig. 28.9 shows graphic dependency|ψ| 2 off χ at different discrete states, i.e. different quantum numbers. As can be seen from the figure, an electron can be in different places of the potential well with different probabilities. There are points where the probability of finding an electron is generally equal to zero. This differs significantly from the ideas of classical physics, according to which it is equally probable that a particle is located in different places of the potential well (Fig. 28.10) and it is impossible to divide the well by points in which the presence of a particle is excluded.

The Schrödinger equation can also be applied to more complex force fields, such as an electron in an atom. This will lead to additional mathematical difficulties, but will not change the main features.

atomic systems: discreteness of energy states, probabilistic judgments about finding an electron, a kind of dependence |ψ| 2 from coordinates, etc.

28.6. APPLICATION OF THE SCHROEDINGER EQUATION TO THE HYDROGEN ATOM. QUANTUM NUMBERS

Describing the states of atoms and molecules using the Schrödinger equation is a rather difficult task. It is most simply solved for one electron located in the field of the nucleus. Such systems correspond to the hydrogen atom and hydrogen-like ions (singly ionized helium atom, doubly ionized lithium atom, etc.). However, in this case, too, the solution of the problem is beyond the scope of our course, so we confine ourselves to a qualitative presentation of the issue.

First of all, the potential energy should be substituted into the Schrödinger equation (28.13), which for two interacting point charges - e(electron) and Ze(core), - located at a distance r in vacuum, is expressed as follows:

With the central symmetry of the field created by the nucleus, it is more convenient to solve the problem not in Cartesian rectangular coordinates, but in spherical r, θ, and p.

The solution to the Schrödinger equation is found as a product of three functions, each of which depends on one variable:

Just as for an electron in a rectangular potential well with infinitely high walls, the boundary conditions lead to specific possible values of ψ and energy, so in the potential well corresponding to the hydrogen atom, the physical conditions lead to possible values of f1, f 2 , f 3 and hence ψ-functions. It also appears here main feature quantum mechanical systems - discreteness of states.

Discreteness mathematically lies in the fact that any of the functions of equation (28.23) has a whole set (spectrum) of solutions, each of which corresponds to a certain quantum number. In contrast to a rectangular potential well with infinitely high walls, the state of an electron in an atom is characterized not by one, but by several quantum numbers 1 . The first of them - principal quantum number P - 1, 2, 3... It determines the energy levels of an electron according to the law:

This expression is a solution of the Schrödinger equation and completely coincides with the corresponding formula of Bohr's theory (see 28.7).

On fig. 28.11 shows the levels of possible values \u200b\u200bof the total energy of the hydrogen atom (E 1, E 2, E 3, etc.) and a graph of the dependence of the potential energy E P on distance r between an electron and a nucleus [see (28.22)]. As the principal quantum number increases P increases r[see, for example, (28.33)], and the complete [see. (28.24)] and the potential energy tends to zero. The kinetic energy also tends to zero. The shaded area (E > 0) corresponds to the state of a free electron.

1 In the general case, quantum numbers are integers (0, 1, 2...) or half-integer (1/2, 3/2, 5/2...) numbers that define possible discrete values physical quantities, which characterize quantum systems and elementary particles.

1 The presence of spin in particles does not follow from the Schrödinger equation.

with this calculation: more time it was in places with a higher probability density, less long - in places with a lower probability density. As a result of the exposure on the film, places of different intensity were obtained, which illustrate the distribution of an electron in an atom. It can be seen from the figures how conditional and even incorrect the concept of “orbit” is in relation to the motion of an electron.

The spin and orbital magnetic moments interact with each other, this changes the system of energy levels of the atom compared to the one that would be without such interaction. It is said that the spin-orbit interaction leads to fine structure energy levels. If it is significant, then it is necessary to take into account the total angular momentum of the electron - orbital plus spin. Meanwhile, instead of m l and m s use other quantum numbers: j and nij.

quantum number j- orbital plus spin - determines the discrete values of the total angular momentum L electron:

Magnetic quantum number m) characterizes the possible projections of the total angular momentum onto some arbitrarily chosen direction Z:

For a given l quantum number j takes two values: ±1/2

(Table 28.1).

Table 28.1

For a given j quantum number nij takes 2j + 1 values: -j, -j + 1 ... + j.

28.7. THE CONCEPT OF THE THEORY OF BORON

Even before the creation of quantum mechanics in 1913, the Danish physicist N. Bohr proposed a theory of the hydrogen atom and hydrogen-like ions, which was based on the nuclear model of the atom and its two postulates. Bohr's postulates did not fit into the framework of classical physics.

According to the first postulate, an atom and atomic systems can stay for a long time only in certain stationary states. Being in such states, the atom does not emit or absorb energy. Stationary states correspond to discrete energy values: E 1, E 2...

Any change in the energy of an atom or atomic system is associated with an abrupt transition from one stationary state to another.

According to the second postulate, during the transition of an atom from one state to another, the atom emits or absorbs a photon, the energy of which is determined by equation (29.1).

The transition from a state with a higher energy to a state with a lower energy is accompanied by the emission of a photon. The reverse process is possible when a photon is absorbed.

According to Bohr's theory, an electron in a hydrogen atom revolves in a circular orbit around the nucleus. Of all the possible orbits, the stationary states correspond only to those for which the angular momentum is an integer h/(2π):

(n = 1, 2, 3...), (28.31)

where m- electron mass; υ η - its speed on nth orbit; rn is its radius. An electron rotating in a circular orbit in an atom is affected by the Coulomb force of attraction from the side of a positively charged nucleus, which, according to Newton's second law, is equal to the product of the electron mass and centripetal acceleration (the record is given for vacuum):

Despite the great success of Bohr's theory, its shortcomings soon became apparent. Thus, within the framework of this theory, it was not possible to explain the difference in the intensities of the spectral lines, i.e. answer the question why some energy transitions are more likely than others. Bohr's theory did not reveal the spectral patterns of a more complex atomic system - the helium atom (two electrons revolving around the nucleus).

The disadvantage of Bohr's theory was its inconsistency. This theory was neither classical nor quantum, it combined the provisions of fundamentally different theories: classical and quantum physics. So, for example, in Bohr's theory, it is believed that an electron rotates in an atom in a certain orbit (classical representations), but it does not emit an electromagnetic wave (quantum representations).

In the first quarter of our century it became clear that Bohr's theory must be replaced by another theory of the atom. Quantum mechanics appeared.

28.8. ELECTRONIC SHELLS OF COMPLEX ATOMS

Quantum numbers describing the state of an electron in a hydrogen atom are used to approximate the state of individual electrons in complex atoms. However, one should take into account at least two significant differences between complex atoms and the hydrogen atom:

1) in complex atoms, the energy of electrons, due to their interaction, depends not only on n, but also on /;

2) the difference is due to the Pauli principle, according to which an atom cannot have two (or more) electrons with four identical quantum numbers.

In the formation of an electronic configuration corresponding to the normal state, each electron of the atom tends to have the lowest energy. If it were not for the Pauli principle, then all electrons would be located at the lowest energy level. In fact, with some exceptions, electrons occupy the sequence of states that is indicated for the hydrogen atom in Table. 29.

Electrons with the same principal quantum number form a layer. The layers are called TO, L M, N etc. in accordance with n= 1, 2, 3, 4... Electrons having the same value pairs n and / , are part of the shell, which is briefly denoted in the same way as the corresponding states for the electron of the hydrogen atom: 1s, 2s, 2^, etc. So, for example, the 2s shell, 2s electrons, etc. are called.

The number of electrons in the shell is indicated at the top right near the symbolic notation of the shell, for example 2p 4 .

The distribution of electrons over shells in an atom (electronic configurations) is usually indicated as follows: for nitrogen 1s 2, 2s2, 2p 3, for calcium 1s 2, 2s 2, 2p 6, 3s 2, 3p 6, 4s 2, etc.

Since the energy of the electrons of complex atoms depends not only on n, but also on l, then the construction of the periodic table does not always occur by the gradual filling of layers as the atom becomes more complex. For potassium (Z = 19), for example, instead of filling the layer M(it could have been 1s 2 , 2s 2 , 2^ 6 , 3s 2 , 3p 6, 3a 1) filling of the layer begins N and create the following electronic configuration: 1 s2, 2s 2, 2p 6, 3s 2, 3p 6, 4s 1.

Other elements also have similar deviations from the regular filling of layers.

Always running general rule: the electrons of an unexcited atom occupy the state with the lowest energy and in accordance with the Pauli principle. On fig. 28.13 schematically, without respect to scale, the energy states of a complex atom and the corresponding number of electrons are shown.

In conclusion, we note that the state of a multielectron atom as a whole is determined by the following quantum numbers: L- the total orbital momentum of the atom, which takes the values 0, 1, 2, 3, etc. one ; J- the total moment of the atom, which can take values with an interval of one from |L - S| to |L + S |; S- the resulting spin moment of the atom; magnetic m J , which determines the discrete values of the projection of the total momentum of the atom onto some axis Z:

For a given Jm J takes 2 J+ 1 values:

-J, -J+ 1 ... +J.

1 Do not confuse this designation with the name of the electronic layer L and with the total angular momentum of the electron.

28.9. ENERGY LEVELS OF MOLECULES

Since molecules are made up of atoms, intramolecular motion is more complicated than intraatomic motion. In a molecule, in addition to the movement of electrons relative to nuclei, oscillating motion atoms around their equilibrium position (vibration of the nuclei together with the electrons surrounding them) and the rotational motion of the molecule as a whole.

Electronic, oscillatory and rotational movements molecules correspond to three types of energy levels: E el, E count and E time. According to quantum mechanics, the energy of all types of motion in a molecule takes only discrete values (quantized). Let us represent approximately the total energy E of the molecule as the sum of quantized values of energies of different types:

E\u003d E el + E count + E time. (28.37)

On fig. 28.14 schematically depicts the level system of a molecule: far-spaced electronic energy levels a" and a"", for which E count = E vr = 0; more closely spaced vibrational levels v" , v"", for them E r = 0; the most closely spaced rotational levels J" and J"" with different values of E time.

Distance between electronic levels energies of the order of several electron volts, between adjacent vibrational levels 10 -2 -10 -1 eV, between adjacent rotational levels 10 -5 -10 -3 eV.

Light has both wave and particle properties. Wave properties appear during the propagation of light (interference, diffraction). Corpuscular properties are manifested in the interaction of light with matter (photoelectric effect, emission and absorption of light by atoms).

The properties of a photon as a particle (energy E and momentum p) are related to its wave properties (frequency ν and wavelength λ) by the relations

; , (19)

where h=6.63×10 -34 J - Planck's constant.

Trying to overcome the difficulties of the Bohr model of the atom, the French physicist Louis de Broglie in 1924 put forward the hypothesis that the combination of wave and corpuscular properties is inherent not only in light, but also in any material body. That is, particles of matter (for example, electrons) have wave properties. suggested, According to de Broglie, each body of mass m, moving with a speed υ, corresponds to a wave process with a wavelength

The most pronounced wave properties are manifested in micro-objects (elementary particles). Due to the small mass, the de Broglie wavelength turns out to be comparable with the interatomic distance in crystals. Under these conditions, the interaction of a particle beam with a crystal lattice gives rise to diffraction phenomena. Electrons with energy 150 eV corresponds to the wavelength λ»10 -10 m. Interatomic distances in crystals are of the same order. If a beam of such electrons is directed to a crystal, then they will scatter according to the laws of diffraction. The diffraction pattern (electron diffraction pattern) recorded on photographic film contains information about the structure of the three-dimensional crystal lattice.

Figure 6 Illustration of the wave properties of matter

To illustrate the wave properties of particles, a thought experiment is often used - the passage of an electron beam (or other particles) through a slot of width Δx. From the point of view of new theory after diffraction by the slit, the beam will broaden with an angular divergence θ»λ/Δх. From the corpuscular point of view, the broadening of the beam after passing through the slit is explained by the appearance of a certain transverse momentum in the particles. The spread in the values of this transverse momentum ("uncertainty") is

(21)

Ratio (22)

is called the uncertainty relation. This ratio in corpuscular language reflects the presence of wave properties in particles.

An experiment on the passage of an electron beam through two closely spaced slits can serve as an even clearer illustration of the wave properties of particles. This experiment is analogous to Young's optical interference experiment.

4. 10 Quantum model of the atom Experimental facts (electron diffraction, the Compton effect, the photoelectric effect, and many others) and theoretical models, such as the Bohr model of the atom, clearly show that the laws of classical physics become inapplicable for describing the behavior of atoms and molecules and their interaction with light. During the decade between 1920 and 1930 a number of prominent physicists of the twentieth century. (de Broglie, Heisenberg, Born, Schrödinger, Bohr, Pauli, etc.) was engaged in the construction of a theory that could adequately describe the phenomena of the microworld. As a result, quantum mechanics was born, which became the basis of all modern theories of the structure of matter, one might say, the basis (together with the theory of relativity) of physics of the twentieth century.

The laws of quantum mechanics are applicable in the microcosm, at the same time we are macroscopic objects and live in the macrocosm governed by completely different, classical laws. Therefore, it is not surprising that many of the provisions of quantum mechanics cannot be verified by us directly and are perceived as strange, impossible, unusual. Nevertheless, quantum mechanics is probably the most experimentally confirmed theory, since the consequences of calculations performed according to the laws of this theory are used in almost everything that surrounds us and have become part of human civilization (suffice it to mention those semiconductor elements, work which currently allow the reader to see the text on the monitor screen, the coverage of which, by the way, is also calculated using quantum mechanics).

Unfortunately, the mathematical apparatus used by quantum mechanics is rather complicated, and the ideas of quantum mechanics can only be stated verbally and therefore not convincingly enough. With this remark in mind, we will try to give at least some idea of these ideas.

The basic concept of quantum mechanics is the concept of the quantum state of some micro-object, or micro-system (it can be a single particle, atom, molecule, set of atoms, etc.).

Quantum model of the atom differs from the planetary one in the first place in that the electron in it does not have a precisely defined coordinate and speed, so it makes no sense to talk about the trajectory of its movement. It is possible to determine (and draw) only the boundaries of the region of its predominant movement (orbitals).

The state of some micro-object or micro-system (it can be a separate particle, atom, molecule, set of atoms, etc.) can be characterized by setting quantum numbers: values of energy, momentum, moment of momentum, projection of this moment of momentum onto some axle, charge, etc.

SCHROEDINGER EQUATION for the motion of an electron in the Coulomb field of the nucleus of the hydrogen atom is used to analyze the quantum model of the atom. As a result of solving this equation, a wave function is obtained, which depends not only on the coordinate and time t, but also on 4 parameters that have a discrete set of values and are called quantum numbers. They have names: principal, azimuthal, magnetic and magnetic spin.

Principal quantum number n can take integer values 1, 2, ... . It determines the energy of an electron in an atom

Where E i is the ionization energy of the hydrogen atom (13.6 eV).

AZIMUTHAL (ORBITAL) quantum number l determines the modulus of the angular momentum of an electron during its orbital motion (24) where s is the spin quantum number, which has only one value for each particle. For example, for an electron s = (similarly, for a proton and a neutron). For a photon, s = 1.

Degenerate states of an electron with the same energy are called.

MULTIPLE DEGENERATION is equal to the number of states with the same energy.

BRIEF recording the state of an electron in an atom: NUMBER, equal to the main quantum number, and the letter that determines the azimuthal quantum number:

Table 1 Brief record of the state of an electron in an atom

Of course, you can call it nonsense,
but I have met such nonsense that in
compared to her, this one seems sensible
dictionary.
L. Carroll

What's happened planetary model atom and what is its disadvantage? What is the essence of the Bohr model of the atom? What is the hypothesis about the wave properties of particles? What predictions does this hypothesis give about the properties of the microworld?

Lesson-lecture

CLASSICAL MODELS OF THE ATOM AND THEIR DISADVANTAGES. The ideas that atoms are not indivisible particles and contain elementary charges as constituent particles were first expressed in late XIX v. The term "electron" was proposed in 1881 by the English physicist George Stoney. In 1897, the electron hypothesis received experimental confirmation in the studies of Emil Wiechert and Joseph John Thomson. From that moment, the creation of various electronic models of atoms and molecules began.

Thomson's first model assumed that the positive charge was evenly distributed throughout the atom, and electrons were interspersed in it, like raisins in a bun.

The discrepancy between this model and the experimental data became clear after an experiment in 1906 by Ernest Rutherford, who studied the process of scattering of α-particles by atoms. From the experience it was concluded that the positive charge is concentrated inside the formation, much smaller than the size of the atom. This formation is called atomic nucleus, the dimensions of which were 10 -12 cm, and the dimensions of the atom - 10 -8 cm. In accordance with the classical ideas of electromagnetism, the Coulomb force of attraction must act between each electron and the nucleus. The dependence of this force on distance should be the same as in the law gravity. Therefore, the movement of electrons in an atom must be similar to the movement of planets. solar system. So was born planetary model of the atom Rutherford.

The short lifetime of an atom and the continuous spectrum of radiation, which follow from the planetary model, showed its inconsistency in describing the motion of electrons in an atom.

Further study of the stability of the atom gave a stunning result: the calculations showed that in a time of 10 -9 s, the electron must fall on the nucleus due to the loss of energy for radiation. In addition, such a model gave continuous rather than discrete emission spectra of atoms.

BORON ATOM THEORY. The next important step in the development of the theory of atoms was made by Niels Bohr. The most important hypothesis put forward by Bohr in 1913 was the hypothesis of the discrete structure of the energy levels of an electron in an atom. This position is illustrated in the energy diagrams (Fig. 21). Traditionally, energy diagrams plot energy along the vertical axis.

Rice. 21 Satellite energy in the Earth's gravitational field (a); energy of an electron in an atom (b)

The difference between the motion of a body in a gravitational field (Fig. 21, a) and the motion of an electron in an atom (Fig. 21, b) in accordance with the Bohr hypothesis is that the energy of the body can continuously change, and the energy of an electron with negative values can take the series discrete values shown in the figure as blue segments. These discrete values were called energy levels or, in other words, energy levels.

Of course, the idea of discrete energy levels was taken from Planck's hypothesis. The change in the energy of an electron, in accordance with Bohr's theory, could only occur in a jump (from one energy level to another). During these transitions, a light quantum is emitted (downward transition) or absorbed (upward transition), the frequency of which is determined from the Planck formula hv \u003d E quantum \u003d ΔE of the atom, i.e., the change in the energy of the atom is proportional to the frequency of the emitted or absorbed light quantum.

Bohr's theory perfectly explained the line character of atomic spectra. However, the theory actually did not give an answer to the question about the reason for the discreteness of the levels.

WAVES OF SUBSTANCE. The next step in the development of the theory of the microworld was made by Louis de Broglie. In 1924, he suggested that the motion of microparticles should be described not as classical mechanical motion, but as some kind of wave motion. It is from the laws of wave motion that recipes for calculating various observable quantities must be obtained. So in science along with waves electromagnetic field waves of matter appeared.

The hypothesis about the wave nature of the motion of particles was as bold as Planck's hypothesis about the discrete properties of the field. An experiment directly confirming de Broglie's hypothesis was set up only in 1927. In this experiment, electron diffraction on a crystal was observed, similar to the diffraction of an electromagnetic wave.

Bohr's theory was an important step in understanding the laws of the microworld. It was the first to introduce the provision on discrete values of the energy of an electron in an atom, which corresponded to experience and subsequently became part of quantum theory.

The hypothesis of matter waves made it possible to explain the discrete nature of energy levels. It was known from the theory of waves that a wave limited in space always has discrete frequencies. An example is a wave in such musical instrument like a flute. The sound frequency in this case is determined by the dimensions of the space that the wave is limited to (the dimensions of the flute). It turns out that this is a general property of waves.

But in accordance with Planck's hypothesis, the frequencies of the quantum of an electromagnetic wave are proportional to the energy of the quantum. Consequently, the electron energy must also take discrete values.

The idea of de Broglie turned out to be very fruitful, although, as already mentioned, a direct experiment confirming the wave properties of an electron was carried out only in 1927. hydrogen atom, got all the results that Bohr's theory was capable of giving. In fact, this was the beginning of the modern theory describing the processes in the microcosm, since the wave equation was easily generalized for the most different systems- multi-electron atoms, molecules, crystals.

The development of the theory led to the understanding that the wave corresponding to the particle determines the probability of finding the particle at a given point in space. So the concept of probability entered the physics of the microcosm

According to the new theory, the wave corresponding to the particle completely determines the motion of the particle. But general properties waves are such that the wave cannot be localized at any point in space, i.e., it is meaningless to talk about the coordinates of the particle at a given moment in time. The consequence of this was the complete exclusion from the physics of the microcosm of such concepts as the trajectory of a particle and electron orbits in an atom. A beautiful and visual planetary model of the atom, as it turned out, does not correspond to the real movement of electrons.

All processes in the microcosm have a probabilistic character. Only the probability of a particular process occurring can be determined by calculations.

In conclusion, let's return to the epigraph. Hypotheses about matter waves and field quanta seemed like nonsense to many physicists who were brought up on the traditions of classical physics. The fact is that these hypotheses are deprived of the usual visualization that we have when making observations in the macrocosm. However, the subsequent development of the science of the microworld led to such ideas that ... (see the epigraph to the paragraph).

What experimental facts did Thomson's model of the atom contradict?
What remains of Bohr's model of the atom in modern theory and what has been discarded?
What ideas contributed to de Broglie's hypothesis about the waves of matter?

The shortcomings of Bohr's theory indicated the need to revise the foundations of quantum theory and ideas about the nature of microparticles (electrons, protons, etc.). The question arose of how exhaustive the representation of an electron is in the form of a small mechanical particle, characterized by certain coordinates and a certain speed.

We already know that a kind of dualism is observed in optical phenomena. Along with the phenomena of diffraction, interference (wave phenomena), phenomena are also observed that characterize the corpuscular nature of light (the photoelectric effect, the Compton effect).

In 1924, Louis de Broglie hypothesized that dualism is not a feature of only optical phenomena ,but is universal. Particles of matter also have wave properties .

“In optics,” wrote Louis de Broglie, “for a century, the corpuscular method of consideration was too neglected in comparison with the wave; Has the reverse error been made in the theory of matter? Assuming that particles of matter, along with corpuscular properties, also have wave properties, de Broglie transferred to the case of particles of matter the same rules for the transition from one picture to another, which are valid in the case of light.

If a photon has energy and momentum, then a particle (for example, an electron) moving at a certain speed has wave properties, i.e. particle motion can be considered as wave motion.

According to quantum mechanics, the free motion of a particle with mass m and momentum (where υ is the particle velocity) can be represented as a plane monochromatic wave ( de Broglie wave) with a wavelength

(3.1.1)

propagating in the same direction (for example, in the direction of the axis X) in which the particle moves (Fig. 3.1).

The dependence of the wave function on the coordinate X is given by the formula

(3.1.2)

where - wave number ,a wave vector directed in the direction of wave propagation or along the motion of the particle:

(3.1.3)

In this way, wave vector of a monochromatic wave associated with a freely moving microparticle, proportional to its momentum or inversely proportional to its wavelength.

Since the kinetic energy of a relatively slowly moving particle , then the wavelength can also be expressed in terms of energy:

(3.1.4)

When a particle interacts with some object - with a crystal, molecule, etc. – its energy changes: the potential energy of this interaction is added to it, which leads to a change in the motion of the particle. Accordingly, the nature of the propagation of the wave associated with the particle changes, and this occurs according to the principles common to all wave phenomena. Therefore, the basic geometric regularities of particle diffraction do not differ in any way from the regularities of diffraction of any waves. The general condition for the diffraction of waves of any nature is the commensurability of the incident wave length λ with distance d between scattering centers: .

The hypothesis of Louis de Broglie was revolutionary, even for that revolutionary time in science. However, it was soon confirmed by many experiments.

By the beginning of the 20th century, both phenomena were known in optics that confirmed the presence of wave properties in light (interference, polarization, diffraction, etc.), and phenomena that were explained from the standpoint of corpuscular theory (photoelectric effect, Compton effect, etc.). At the beginning of the 20th century, a number of effects were discovered for particles of matter, outwardly similar to optical phenomena characteristic of waves. So, in 1921, Ramsauer, while studying the scattering of electrons on argon atoms, found that as the electron energy decreases from several tens of electron volts, the effective cross section for elastic scattering of electrons on argon increases (Figure 4.1).

But at an electron energy of ~16 eV, the effective cross section reaches a maximum and decreases with a further decrease in the electron energy. At an electron energy of ~ 1 eV, it becomes close to zero, and then begins to increase again.

Thus, near ~ 1 eV, electrons do not seem to experience collisions with argon atoms and fly through the gas without scattering. The same behavior is also characteristic of the cross section for electron scattering by other atoms of inert gases, as well as by molecules (the latter was discovered by Townsend). This effect is analogous to the formation of a Poisson spot during light diffraction on a small screen.

Another interesting effect is the selective reflection of electrons from the surface of metals; it was studied in 1927 by the American physicists Davisson and Germer, and also independently by the English physicist J.P. Thomson.

A parallel beam of monoenergetic electrons from a cathode ray tube (Figure 4.2) was directed onto a nickel plate. The reflected electrons were captured by a collector connected to a galvanometer. The collector is installed at any angle relative to the incident beam (but in the same plane with it).

As a result of the Davisson-Jermer experiments, it was shown that the angular distribution of scattered electrons has the same character as the distribution of X-rays scattered by a crystal (Figure 4.3). When studying the diffraction of X-rays on crystals, it was found that the distribution of diffraction maxima is described by the formula

where is the lattice constant, is the diffraction order, is the X-ray wavelength.

In the case of neutron scattering by a heavy nucleus, a typical diffraction distribution of scattered neutrons also arose, similar to that observed in optics when light is diffracted by an absorbing disk or ball.

The French scientist Louis de Broglie in 1924 expressed the idea that the particles of matter have both corpuscular and wave properties. At the same time, he suggested that a particle moving freely at a constant speed corresponds to a plane monochromatic wave

where and are its frequency and wave vector.

Wave (4.2) propagates in the direction of motion of the particle (). Such waves are called phase waves, matter waves or de Broglie waves.

De Broglie's idea was to expand the analogy between optics and mechanics, and to compare wave optics with wave mechanics, trying to apply the latter to intra-atomic phenomena. An attempt to attribute to an electron, and in general to all particles, like photons, dual nature, endowing them with wave and corpuscular properties interconnected by a quantum of action - such a task seemed extremely necessary and fruitful. “... It is necessary to create a new mechanics of a wave nature, which will relate to the old mechanics as wave optics to geometric optics,” de Broglie wrote in his book “Revolution in Physics”.

A particle of mass moving at a speed has energy

and momentum

and the state of particle motion is characterized by a four-dimensional energy-momentum vector ().

On the other hand, in the wave pattern we use the concept of frequency and wave number (or wavelength), and the 4-vector corresponding to a plane wave is ().

Since both of the above descriptions are different aspects of the same physical object, there must be an unambiguous relationship between them; the relativistically invariant relation between 4-vectors is

Expressions (4.6) are called de Broglie formulas. The de Broglie wavelength is thus determined by the formula

(here). It is this wavelength that should appear in the formulas for the wave description of the Ramsauer-Townsend effect and the Davisson-Jermer experiments.

For electrons accelerated electric field with potential difference B, de Broglie wavelength nm; at kV = 0.0122 nm. For a hydrogen molecule with energy J (at = 300 K) = 0.1 nm, which coincides in order of magnitude with the wavelength of X-rays.

Taking into account (4.6), formula (4.2) can be written as a plane wave

the corresponding particle with momentum and energy.

De Broglie waves are characterized by phase and group velocities. Phase speed is determined from the condition of constancy of the phase of the wave (4.8) and for a relativistic particle is equal to

that is, it is always greater than the speed of light. group speed de Broglie waves is equal to the speed of the particle:

From (4.9) and (4.10) the relationship between the phase and group velocities of de Broglie waves follows:

What is physical meaning de Broglie waves and what is their relationship with particles of matter?

Within the framework of the wave description of the motion of a particle, a significant epistemological complexity was presented by the question of its spatial localization. De Broglie waves (4.2), (4.8) fill the entire space and exist for an unlimited time. The properties of these waves are always and everywhere the same: their amplitude and frequency are constant, the distances between the wave surfaces are unchanged, etc. On the other hand, microparticles retain their corpuscular properties, that is, they have a certain mass localized in a certain region of space. In order to get out of this situation, particles began to be represented not by monochromatic de Broglie waves, but by sets of waves with close frequencies (wave numbers) - wave packets:

in this case, the amplitudes are nonzero only for waves with wave vectors contained in the interval (). Since the group velocity of the wave packet is equal to the velocity of the particle, it was proposed to represent the particle in the form of a wave packet. But this idea is untenable for the following reasons. A particle is a stable formation and does not change as such during its motion. The wave packet that claims to represent a particle must have the same properties. Therefore, it is necessary to require that, over time, the wave packet retains its spatial shape, or at least its width. However, since the phase velocity depends on the momentum of the particle, then (even in a vacuum!) There must be a dispersion of de Broglie waves. As a result, the phase relationships between the waves of the packet are violated, and the packet spreads. Therefore, the particle represented by such a packet must be unstable. This conclusion is contrary to experience.

Further, the opposite assumption was put forward: particles are primary, and waves represent their formations, that is, they arise, like sound in a medium consisting of particles. But such a medium must be sufficiently dense, because it makes sense to talk about waves in a medium of particles only when the average distance between particles is very small compared to the wavelength. And in experiments in which the wave properties of microparticles are found, this is not performed. But even if this difficulty is overcome, the indicated point of view must still be rejected. Indeed, it means that wave properties are inherent in systems of many particles, and not in individual particles. Meanwhile, the wave properties of the particles do not disappear even at low intensities of the incident beams. In the experiments of Biberman, Sushkin and Fabrikant, carried out in 1949, such weak electron beams were used that the average time interval between two successive passages of an electron through a diffraction system (crystal) was 30,000 (!) times longer than the time spent by one electron to pass through the entire device. Under such conditions, the interaction between the electrons, of course, played no role. Nevertheless, with a sufficiently long exposure, a diffraction pattern appeared on a photographic film placed behind the crystal, which did not differ in any way from the pattern obtained with a short exposure to electron beams, the intensity of which was 10 7 times greater. It is only important that in both cases total number electrons hitting the photographic plate were the same. This shows that individual particles also have wave properties. The experiment shows that one particle does not give a diffraction pattern; each individual electron causes blackening of the photographic plate in a small area. The entire diffraction pattern can be obtained only by hitting the plate a large number particles.

The electron in the considered experiment completely retains its integrity (charge, mass and other characteristics). This shows its corpuscular properties. At the same time, the manifestation of wave properties is also evident. The electron never hits that section of the photographic plate where there should be a minimum of the diffraction pattern. It can only appear near the position of the diffraction maxima. In this case, it is impossible to specify in advance in which specific direction a given particle will fly.

The idea that both corpuscular and wave properties are manifested in the behavior of micro-objects is enshrined in the term "particle-wave dualism" and underlies quantum theory, where he received a natural interpretation.

Born proposed the following now generally accepted interpretation of the results of the described experiments: the probability of an electron hitting a certain point on a photographic plate is proportional to the intensity of the corresponding de Broglie wave, that is, to the square of the wave field amplitude at a given location on the screen. Thus, it is proposed probabilistic-statistical interpretation the nature of the waves associated with microparticles: the regularity of the distribution of microparticles in space can be established only for a large number of particles; for one particle, only the probability of hitting a certain area can be determined.

After getting acquainted with the corpuscular-wave dualism of particles, it is clear that those methods that are used in classical physics are unsuitable for describing the mechanical state of microparticles. In quantum mechanics, new specific means must be used to describe the state. The most important of these is the concept of wave function, or state function (-functions).

The state function is mathematical image of the wave field that should be associated with each particle. Thus, the state function of a free particle is a plane monochromatic de Broglie wave (4.2) or (4.8). For a particle subjected to external action (for example, for an electron in the field of a nucleus), this wave field can have a very complex form, and it changes with time. The wave function depends on the parameters of the microparticle and on the physical conditions in which the particle is located.

Further, we will see that through the wave function, the most Full description mechanical state of a micro-object, which is only possible in the micro-world. Knowing the wave function, it is possible to predict which values of all measured quantities can be observed experimentally and with what probability. The state function carries all the information about the motion and quantum properties of particles; therefore, one speaks of setting a quantum state with its help.

According to the statistical interpretation of de Broglie waves, the probability of particle localization is determined by the intensity of the de Broglie wave, so that the probability of detecting a particle in a small volume in the vicinity of a point at a time is

Taking into account the complexity of the function, we have:

For a plane de Broglie wave (4.2)

that is, it is equally likely to find a free particle anywhere in space.

the value

called probability density. Probability of finding a particle at a time in a finite volume, according to the probability addition theorem, is equal to

If we integrate in (4.16) in infinite limits, we will get full probability detecting a particle at a point in time somewhere in space. This is the probability of a certain event, so

Condition (4.17) is called normalization condition, and - a function that satisfies it, - normalized.

We emphasize once again that for a particle moving in a force field, the function is more complex type than the de Broglie plane wave (4.2).

Since the -function is complex, it can be represented as

where is the modulus of the -function, and is the phase factor, in which is any real number. From the joint consideration of this expression and (4.13) it is clear that the normalized wave function is defined ambiguously, but only up to a constant factor. The noted ambiguity is fundamental and cannot be eliminated; however, it is insignificant, since it does not affect any physical results. Indeed, multiplying a function by an exponent changes the phase of the complex function, but not its modulus, which determines the probability of obtaining one or another value of a physical quantity in an experiment.

The wave function of a particle moving in a potential field can be represented by a wave packet. If, when a particle moves along an axis, the length of the wave packet is equal, then the wave numbers necessary for its formation cannot occupy an arbitrarily narrow interval. The minimum interval width must satisfy the relation or, after multiplying by,

Similar relationships hold for wave packets propagating along the axes and:

Relations (4.18), (4.19) are called Heisenberg uncertainty relations(or uncertainty principle). According to this fundamental position of quantum theory, any physical system cannot be in states in which the coordinates of its center of inertia and momentum simultaneously take on quite definite, exact values.

Relations similar to those written down must hold for any pair of so-called canonically conjugate quantities. Planck's constant contained in the uncertainty relations sets a limit on the accuracy of the simultaneous measurement of such quantities. At the same time, the uncertainty in measurements is connected not with the imperfection of the experimental technique, but with the objective (wave) properties of matter particles.

Another important point in considering the states of microparticles is the effect of the device on the microobject. Any measurement process leads to a change in the physical parameters of the state of the microsystem; the lower limit of this change is also set by the uncertainty relation.

In view of the smallness in comparison with macroscopic quantities of the same dimension, the effects of the uncertainty relations are significant mainly for atomic and smaller scale phenomena and do not appear in experiments with macroscopic bodies.

Uncertainty relations, first obtained in 1927 by the German physicist W. Heisenberg, were an important step in elucidating the patterns of intra-atomic phenomena and building quantum mechanics.

As follows from the statistical interpretation of the meaning of the wave function, a particle can be detected with some probability at any point in space where the wave function is nonzero. Therefore, the results of experiments on measurement, for example, coordinates, are of a probabilistic nature. This means that when conducting a series of identical experiments on identical systems (that is, when reproducing the same physical conditions), different results are obtained each time. However, some values will be more likely than others and will appear more frequently. Most often, those values of the coordinate will be obtained that are close to the value that determines the position of the maximum of the wave function. If the maximum is clearly expressed (the wave function is a narrow wave packet), then the particle is mainly located near this maximum. Nevertheless, some scatter in the values of the coordinate (an uncertainty of the order of the half-width of the maximum) is unavoidable. The same applies to the measurement of momentum.

In atomic systems, the magnitude is equal in order of magnitude to the area of the orbit along which, in accordance with the Bohr-Sommerfeld theory, a particle moves in the phase plane. This can be verified by expressing the area of the orbit in terms of the phase integral. In this case, it turns out that the quantum number (see lecture 3) satisfies the condition

In contrast to the Bohr theory, where equality takes place (here is the electron velocity in the first Bohr orbit in the hydrogen atom, is the speed of light in vacuum), in the considered case in stationary states, the average momentum is determined by the dimensions of the system in the coordinate space, and the ratio is only in order of magnitude. Thus, using coordinates and momentum to describe microscopic systems, it is necessary to introduce quantum corrections into the interpretation of these concepts. Such a correction is the uncertainty relation.

The uncertainty relation for energy and time has a slightly different meaning:

If the system is in a stationary state, then it follows from the uncertainty relation that the energy of the system, even in this state, can only be measured with an accuracy not exceeding, where is the duration of the measurement process. Relation (4.20) is also valid if we understand the uncertainty of the value of the energy of the non-stationary state of a closed system, and by - the characteristic time during which the average values of physical quantities in this system change significantly.

The uncertainty relation (4.20) leads to important conclusions regarding the excited states of atoms, molecules, and nuclei. Such states are unstable, and it follows from the uncertainty relation that the energies of the excited levels cannot be strictly defined, that is, the energy levels have some natural width, where is the lifetime of the excited state. Another example is the alpha decay of a radioactive nucleus. The energy spread of the emitted -particles is related to the lifetime of such a nucleus by the relation.

For the normal state of the atom, and energy has a well-defined value, that is. For an unstable particle s, and there is no need to talk about a certain value of its energy. If the lifetime of an atom in an excited state is taken equal to c, then the width of the energy level is ~10 -26 J and the width of the spectral line that occurs during the transition of an atom to the normal state, ~10 8 Hz.

It follows from the uncertainty relations that the division of the total energy into kinetic and potential loses its meaning in quantum mechanics. Indeed, one of them depends on the momenta, and the other - on the coordinates. The same variables cannot have certain values at the same time. Energy should be defined and measured only as total energy, without division into kinetic and potential.