The theorem of multiplying the probabilities of two arbitrary events: the probability of the product of two arbitrary events is equal to the product of the probability of one of the events by the conditional probability of the other event, provided that the first has already happened:

P(AB)=P(A)P(B|A) = P(B)P(A|B). (10)

Proof (not rigorous): we will prove the multiplication theorem for the scheme of chances (equiprobable hypotheses). Let the possible outcomes of the experience be n chances. Assume that event A has m chances (shaded in Fig. 11); event B - k chances; simultaneously events A and B (AB) - l chances (in Fig. 11 they have light shading).

Figure 11

Obviously, m+k-l=n. According to the classical way of calculating the probabilities P(AB)=l/n; P(A)=m/n; P(B)=k/n. And the probability is P(B|A)=l/m, since it is known that one of the m chances of event A has occurred, and event B is favored by l similar chances. Substituting these expressions into theorem (10), we obtain the identity l/n=(m/n)(l/m). The theorem has been proven.

The probabilities multiplication theorem for three arbitrary events:

P(ABC)=|AB=D|=P(DC)=P(D)P(C|D)=P(AB)P(C|AB)=P(A)P(B|A)P( C|AB).(11)

By analogy, one can write probability multiplication theorems for more events.

Corollary 1. If event A does not depend on B, then event B does not depend on A either.

Proof. Because event A does not depend on B, then by the definition of independence of events P(A)=P(A|B)=P(A|). It is required to prove that P(B)=P(B|A).

By the multiplication theorem, P(AB)=P(A)P(B|A)=P(B)P(A|B), therefore, P(A)P(B|A)=P(B)P(A ). Assuming that P(A)>0, we divide both sides of the equality by P(A) and get: P(B)=P(B|A).

Corollary 1 implies that two events are independent if the occurrence of one of them does not change the probability of the occurrence of the other. In practice, events (phenomena) that are interconnected by a causal relationship are dependent.

Corollary 2. Probability of product of two independent events is equal to the product of the probabilities of these events. Those. if events A and B are independent, then

P(AB)=P(A)P(B). (eleven)

The proof is obvious, since for independent events P(B|A)=P(B).

Identity (11), along with expressions (12) and (13), are necessary and sufficient conditions for the independence of two random events A and B.

P(A)=P(A|B); P(A)=P(A|); P(A|B)=P(A|); (12)

P(B)=P(B|A); P(B)=P(B|); P(B|A)=P(B|). (thirteen)

The reliability of some system is increased by double redundancy (see Fig. 12). The probability of failure-free operation of the first subsystem (during some operating time) is 0.9, the second - 0.8. Determine the probability of failure of the system as a whole during a given operating time, if the failures of the subsystems are independent.

Figure 12 - Double redundant system

E: Reliability study of a doubly redundant control system;

A 1 =(non-failure operation (during some operating time) of the first subsystem); P(A1)=0.9;

A 2 =(failsafe operation of the second subsystem); P(A2)=0.8;

A=(failsafe operation of the system as a whole); P(A)=?

Solution. Let us express the event A in terms of the events A 1 and A 2 whose probabilities are known. Since the failure-free operation of at least one of its subsystems is sufficient for the failure-free operation of the system, it is obvious that A=A 1 A 2.

Applying the probability addition theorem, we get: P(A)=P(A 1 A 2)=P(A 1)+P(A 2)-P(A 1 A 2). The probability of the joint occurrence of events A 1 and A 2 is determined by the probability multiplication theorem: P(A 1 A 2)=P(A 1)P(A 2 |A 1). Considering that (by condition) the events A 1 and A 2 are independent, P(A 1 A 2)=P(A 1)P(A 2). Thus, the probability of failure-free operation of the system is P(A)=P(A 1 A 2)=P(A 1)+P(A 2)-P(A 1)P(A 2)=0.9+0, 8-0.90.8=0.98.

Answer: the probability of failure-free operation of the system during a given operating time is 0.98.

Comment. In example 20, another way of defining event A is possible through events A 1 and A 2: , i.e. A system failure is possible when both of its subsystems fail simultaneously. Applying the theorem of multiplication of probabilities of independent events, we obtain the following value of the probability of system failure: . Therefore, the probability of failure-free operation of the system during a given operating time is equal to.

Example 21 (paradox of independence)

E: Two coins are tossed.

A=(coat of arms loss on the first coin), P(A)=0.5;

B=(coat of arms loss on the second coin), P(B)=0.5;

C=(coat of arms appearing on only one of the coins), P(C)=0.5.

Events A, B and C are pairwise independent, since the conditions for the independence of two events (11)-(13) are satisfied:

P(A)=P(A|B)=0.5; P(B)=P(B|C)=0.5; P(C)=P(C|A)=0.5.

However, P(A|BC)=0P(A); P(A|C)=1P(A); P(B|AC)=0P(B); P(C|AB)=0P(C).

Comment. Pairwise independence of random events does not mean their independence in the aggregate.

Random events are collectively independent if the probability of occurrence of each of them does not change with the occurrence of any combination of other events. For random events A 1, A 2, ... A n, independent in the aggregate, the following probability multiplication theorem is valid (a necessary and sufficient condition for independence in the aggregate of n random events):

P(A 1 A 2 ... A n) \u003d P (A 1) P (A 2) ... P (A n). (14)

For example 21, condition (14) is not satisfied: P(ABC)=0P(A)P(B)P(C)=0.50.50.5=0.125. Therefore, pairwise independent events A, B and C are mutually dependent.

Example 22

There are 12 transistors in the box, three of which are faulty. To assemble a two-stage amplifier, two transistors are randomly removed. What is the probability that the assembled amplifier will be faulty?

E: selection of two transistors from the box with 9 good and 3 bad transistors;

A=(faulty assembled amplifier); P(A)=?

Solution. Obviously, the assembled two-stage amplifier will be faulty if at least one of the two transistors selected for assembly is faulty. Therefore, we redefine event A as follows:

A=(at least one of the two selected transistors is faulty);

Let us define the following auxiliary random events:

A 01 = (only the first of the two selected transistors is faulty);

A 10 = (only the second of the two selected transistors is faulty);

A 00 = (both selected transistors are faulty);

Obviously, A=A 01 A 10 A 00 (for the event A to occur, at least one of the events A 01 or A 10 or A 00 must occur), and the events A 01, A 10 and A 00 are incompatible (they cannot occur together) , so we find the probability of an event using the probability addition theorem incompatible events:

P(A)=P(A 01 A 10 A 00)=P(A 01)+P(A 10)+P(A 00).

To determine the probabilities of events A 01, A 10 and A 00, we introduce auxiliary events:

B 1 =(the first selected transistor is defective);

B 2 =(Second selected transistor is defective).

It is obvious that A 01 =B 1 ; A 10 = B 2 ; A 00 = B 1 B 2 ; therefore, to determine the probabilities of events A 01, A 10 and A 00, we apply the probabilities multiplication theorem.

P(A 01)=P(B 1)=P(B 1)P(|B 1),

where P(B 1) is the probability that the first selected transistor will be faulty; P(|B 1) - the probability that the second selected transistor will be good, provided that the first selected transistor is faulty. Using the classic way of calculating probabilities, P(B 1)=3/12, and P(|B 1)=9/11 (because after choosing the first bad transistor, there are 11 transistors left in the box, 9 of which are good).

Thus, P(A 01)=P(B 1)=P(B 1)P(|B 1)=3/129/11=0.20(45). Similarly:

P(A 10)=P(B 2)=P()P(B 2 |)=9/123/11=0.20(45);

P(A 00)=P(B 1 B 2)=P(B 1)P(B 2 |B 1)=3/122/11=0.041(6).

Let us substitute the obtained values ​​of the probabilities A 01, A 10 and A 00 into the expression for the probability of the event A:

P(A)=P(A 01 A 10 A 00)=P(A 01)+P(A 10)+P(A 00)=3/129/11+9/123/11+3/122/11 =0.45(45).

Answer: The probability that the assembled amplifier will be faulty is 0.4545.

Educational Institution "Belarusian State

agricultural Academy"

Department of Higher Mathematics

ADDITION AND MULTIPLICATION OF PROBABILITIES. REPEATED INDEPENDENT TESTS

Lecture for students of the Faculty of Land Management

distance learning

Gorki, 2012

Addition and multiplication of probabilities. Repeated

independent tests

1. Addition of probabilities

The sum of two joint events A and V called an event WITH, consisting in the occurrence of at least one of the events A or V. Similarly, the sum of several joint events is an event consisting in the occurrence of at least one of these events.

The sum of two disjoint events A and V called an event WITH, consisting in the occurrence or event A, or events V. Similarly, the sum of several incompatible events is an event consisting in the occurrence of any one of these events.

The theorem of addition of probabilities of incompatible events is valid: the probability of the sum of two incompatible events is equal to the sum of the probabilities of these events , i.e. . This theorem can be extended to any finite number of incompatible events.

From this theorem follows:

the sum of the probabilities of events forming a complete group is equal to one;

the sum of the probabilities of opposite events is equal to one, i.e.
.

Example 1 . A box contains 2 white, 3 red and 5 blue balls. The balls are shuffled and one is drawn at random. What is the probability that the ball is colored?

Solution . Let's denote the events:

A=(color ball removed);

B=(white ball drawn);

C=(red ball drawn);

D=(blue ball removed).

Then A= C+ D. Since the events C, D are incompatible, then we use the theorem of addition of probabilities of incompatible events: .

Example 2 . An urn contains 4 white balls and 6 black balls. 3 balls are drawn at random from the urn. What is the probability that they are all the same color?

Solution . Let's denote the events:

A\u003d (balls of the same color are taken out);

B\u003d (white balls are taken out);

C= (black balls are taken out).

Because A= B+ C and events V and WITH are incompatible, then by the theorem of addition of probabilities of incompatible events
. Event Probability V is equal to
, where
4,

. Substitute k and n into the formula and get
Similarly, we find the probability of an event WITH:
, where
,
, i.e.
. Then
.

Example 3 . From a deck of 36 cards, 4 cards are drawn at random. Find the probability that there will be at least three aces among them.

Solution . Let's denote the events:

A\u003d (among the drawn cards there are at least three aces);

B\u003d (among the drawn cards there are three aces);

C= (among the drawn cards there are four aces).

Because A= B+ C, and the events V and WITH inconsistent, then
. Let's find the probabilities of events V and WITH:

,
. Therefore, the probability that among the drawn cards there are at least three aces is equal to

0.0022.

1. Probability multiplication

work two events A and V called an event WITH, consisting in the joint occurrence of these events:
. This definition extends to any finite number of events.

The two events are called independent if the probability of occurrence of one of them does not depend on whether the other event occurred or not. Events , , … , called collectively independent , if the probability of occurrence of each of them does not depend on whether other events occurred or did not occur.

Example 4 . Two arrows shoot at a target. Let's denote the events:

A=(first shooter hit the target);

B= (the second shooter hit the target).

Obviously, the probability of hitting the target by the first shooter does not depend on whether the second shooter hit or missed, and vice versa. Therefore, the events A and V independent.

The theorem of multiplication of probabilities of independent events is valid: the probability of the product of two independent events is equal to the product of the probabilities of these events : .

This theorem is also valid for n events that are independent in the aggregate: .

Example 5 . Two shooters shoot at the same target. The probability of hitting the first shooter is 0.9, and the second is 0.7. Both shooters fire one shot at the same time. Determine the probability that there will be two hits on the target.

Solution . Let's denote the events:

A

B

C=(both arrows will hit the target).

Because
, and the events A and V independent, then
, i.e. .

Events A and V called dependent if the probability of occurrence of one of them depends on whether the other event occurred or not. Probability of an event A provided that the event V it's already here, it's called conditional probability and denoted
or
.

Example 6 . An urn contains 4 white and 7 black balls. Balls are drawn from the urn. Let's denote the events:

A=(white ball removed) ;

B=(black ball removed).

Before you start drawing balls from the urn
. One ball is drawn from the urn and it turns out to be black. Then the probability of the event A after the event V will be different, equal . This means that the probability of an event A event dependent V, i.e. these events will be dependent.

The theorem of multiplication of probabilities of dependent events is valid: the probability of the product of two dependent events is equal to the product of the probability of one of them by the conditional probability of the other, calculated on the assumption that the first event has already occurred, i.e. or .

Example 7 . An urn contains 4 white balls and 8 red balls. Two balls are drawn at random from it. Find the probability that both balls are black.

Solution . Let's denote the events:

A=(black ball drawn first);

B=(a black ball is drawn second).

Events A and V dependent because
, a
. Then
.

Example 8 . Three arrows shoot at the target independently of each other. The probability of hitting the target for the first shooter is 0.5, for the second - 0.6 and for the third - 0.8. Find the probability that two hits will occur if each shooter fires one shot.

Solution . Let's denote the events:

A=(there will be two hits on the target);

B=(first shooter hits the target);

C=(the second shooter will hit the target);

D=(the third shooter will hit the target);

=(the first shooter will not hit the target);

=(the second shooter will not hit the target);

=(the third shooter will not hit the target).

According to the example
,
,
,

,
,
. Since , then using the addition theorem for the probabilities of incompatible events and the theorem for multiplying the probabilities of independent events, we get:

Let the events
form a complete group of events of some trial, and the events A can only occur with one of these events. If the probabilities and conditional probabilities of an event are known A, then the probability of event A is calculated by the formula:

Or
. This formula is called formula full probability , and the events
hypotheses .

Example 9 . The assembly line receives 700 parts from the first machine and 300 parts from the second. The first machine gives 0.5% rejects, and the second - 0.7%. Find the probability that the item taken is defective.

Solution . Let's denote the events:

A=(the item taken will be defective);

= (the part is made on the first machine);

= (the part is made on the second machine).

The probability that the part was made on the first machine is
. For the second machine
. By the condition, the probability of obtaining a defective part made on the first machine is equal to
. For the second machine, this probability is equal to
. Then the probability that the part taken will be defective is calculated by the total probability formula

If an event is known to have occurred as a result of a test A, then the probability that this event occurred with the hypothesis
, is equal to
, where
- total probability of the event A. This formula is called Bayes formula and allows you to calculate the probabilities of events
after it became known that the event A has already arrived.

Example 10 . Parts of the same type for cars are produced at two factories and go to the store. The first plant produces 80% of the total number of parts, and the second - 20%. The production of the first plant contains 90% of standard parts, and the second - 95%. The buyer bought one part and it turned out to be standard. Find the probability that this part is made in the second factory.

Solution . Let's denote the events:

A=(purchased a standard part);

= (the part is made at the first factory);

= (the part is made at the second factory).

According to the example
,
,
and
. Calculate the total probability of an event A: 0.91. The probability that the part is manufactured at the second plant is calculated using the Bayes formula:

.

Tasks for independent work

The probability of hitting the target for the first shooter is 0.8, for the second - 0.7 and for the third - 0.9. The shooters fired one shot. Find the probability that there are at least two hits on the target.

The repair shop received 15 tractors. It is known that 6 of them need to replace the engine, and the rest - to replace individual components. Three tractors are randomly selected. Find the probability that no more than two selected tractors need an engine replacement.

The concrete plant produces panels, 80% of which are of the highest quality. Find the probability that out of three randomly selected panels, at least two will be of the highest grade.

Three workers assemble bearings. The probability that the bearing assembled by the first worker is of the highest quality is 0.7, the second - 0.8, and the third - 0.6. For control, one bearing was taken at random from those assembled by each worker. Find the probability that at least two of them are of the highest quality.

The probability of winning on a lottery ticket of the first issue is 0.2, the second - 0.3 and the third - 0.25. There is one ticket for each issue. Find the probability that at least two tickets will win.

The accountant performs calculations using three reference books. The probability that the data of interest to him is in the first directory is 0.6, in the second - 0.7, and in the third - 0.8. Find the probability that the data of interest to the accountant is contained in no more than two directories.

Three machines make parts. The first automaton produces a part of the highest quality with a probability of 0.9, the second with a probability of 0.7, and the third with a probability of 0.6. One item is taken at random from each machine. Find the probability that at least two of them are of the highest quality.

The same type of parts are processed on two machines. The probability of manufacturing a non-standard part for the first machine is 0.03, for the second - 0.02. The processed parts are stacked in one place. Among them, 67% are from the first machine, and the rest from the second. A randomly taken part turned out to be standard. Find the probability that it was made on the first machine.

The workshop received two boxes of the same type of capacitors. The first box contained 20 capacitors, of which 2 were defective. In the second box there are 10 capacitors, of which 3 are faulty. Capacitors were transferred to one box. Find the probability that a capacitor taken at random from the box is good.

On three machines, the same type of parts are made, which are fed to a common conveyor. Among all the details, 20% from the first machine, 30% from the second and 505 from the third. The probability of manufacturing a standard part on the first machine is 0.8, on the second - 0.6 and on the third - 0.7. The part taken was standard. Find the probability that this part is made on the third machine.

The picker receives 40% of the parts from the factory for assembly A, and the rest - from the factory V. The probability that the part from the factory A- the highest quality, equal to 0.8, and from the factory V– 0.9. The picker randomly took one part and it was not of the highest quality. Find the probability that this part is from the factory V.

10 students from the first group and 8 students from the second were selected to participate in student sports competitions. The probability that a student from the first group will get into the national team of the academy is 0.8, and from the second - 0.7. A randomly selected student was selected for the national team. Find the probability that he is from the first group.

Theorem.(Probability multiplications) The probability of the product of two events (the joint occurrence of these events) is equal to the product of the probability of one of them by the conditional probability of the other, calculated under the condition that the first event has already occurred.

You can also write:

The proof of this theorem follows directly from the definition of conditional probability.

If the events are independent, then , and the probability multiplication theorem takes the form:

In the case of a product of several dependent events, the probability is equal to the product of one of them by the conditional probabilities of all the others, provided that the probability of each subsequent event is calculated on the assumption that all other events have already occurred.

From the probability product theorem, we can conclude that probabilities appearance at least one event .

If the test results in P events that are independent in the aggregate, then the probability of the occurrence of at least one of them is equal to

Here event A indicates the occurrence of at least one of the events A i , a qi is the probability of opposite events.

Example 1 Four cards are taken out at the same time from a full deck of cards (52 pcs.). Find the probability that among these four cards there will be at least one diamond or one heart card.

Solution.

Denote the appearance of at least one diamond card - the event A , the appearance of at least one red card is an event V . Thus, we need to determine the probability of an event WITH = A + V .

In addition, events A and V - joint, i.e. the appearance of one of them does not exclude the appearance of the other.

In total, there are 13 heart and 13 diamond cards in the deck.

Find the probability of an event opposite to the event WITH (among the drawn cards there will be neither diamonds nor hearts):

when the first card is drawn, the probability that neither a red nor a diamond card will appear is , when the second card is drawn - , the third - , the fourth - .

Then the probability that among the drawn cards there will be neither diamonds nor hearts is equal to .

Desired probability

Example 2 What is the probability that when three dice are rolled, a 6 will appear on at least one of the dice?

Solution.

The probability of getting 6 points on a single roll of the die is . The probability of not getting 6 points is . The probability that a roll of three dice will not land a 6 is equal to .

Then the probability that 6 points will fall at least once is equal to .

Example 3 The drum of the revolver contains 4 cartridges out of six in random order. The drum is spun, and then the trigger is pulled twice. Find the probabilities of: a) at least one shot, b) two shots, c) two misfires.

Solution.

Probability of being fired on first pull of the trigger (event A ) is equal to , the probability of a misfire - The probability of a shot at the second pull of the trigger depends on the result of the first pull.

So if in the first case there was a shot, then only 3 cartridges remained in the drum, and they are distributed over 5 slots, because. on the second pull of the trigger, the nest cannot be opposite the barrel, in which the cartridge was at the first pull of the trigger.

The conditional probability of a shot on the second attempt - if the first time there was a shot, - if the first time there was a misfire.

The conditional probability of a misfire for the second time is , if the first time there was a shot, - if there was a misfire the first time.

Consider the probabilities that in the second case a shot will occur (the event V ) or a misfire occurs (event ) provided that in the first case a shot occurred (event A ) or misfire (event ).

Two shots in a row

First misfire, second shot

First shot, second misfire

Two misfires in a row

These four cases form a complete group of events (the sum of their probabilities is equal to one)

Analyzing the obtained results, we see that the probability of at least one shot is equal to the sum

Example 4 Two shooters shoot at a target. The probability of hitting the target with one shot for the first shooter is 0.7, and for the second - 0.8. Find the probability that in one volley only one of the shooters hits the target.

Solution.

Let us designate the first shooter hitting the target - event A, the second - event B, the miss of the first shooter - the event , the miss of the second - the event .

The probability that the first shooter hits the target and the second does not is equal to

The probability that the second shooter will hit the target and the first one will not is equal to

Then the probability of hitting the target by only one shooter is equal to

The same result can be obtained in another way - we find the probabilities that both arrows hit the target and both missed. These probabilities are respectively equal to:

Then the probability that only one shooter hits the target is:

Example 5 The probability that a part taken at random from a certain batch of parts will be defective is 0.2. Find the probability that 2 out of 3 items will be defective.

Solution.

Denote the defective part - event A, not defective - event .

If among the three parts there is only one defective, then this is possible in one of three cases: the defective part will be the first, second or third.

Example 6 The probabilities that the desired part is in the first, second, third or fourth box are 0.6, 0.7, 0.8, 0.9, respectively. Find the probabilities that this part is located: a) in no more than three boxes; b) not less than two boxes.

Solution.

a) The probability that the item is in all four boxes is

The probability that the desired part is in no more than three boxes is equal to the probability that it is not in all four boxes.

b) The probability that the desired part is in at least two boxes is the sum of the probabilities that the part is in only two boxes, only three boxes, only four boxes. Of course, these probabilities can be calculated and then added, however, it is easier to do otherwise. The same probability is equal to the probability that the part is not in only one box and is available at all.

Let A and V are the two events considered in this test. In this case, the occurrence of one of the events may affect the possibility of the occurrence of another. For example, the occurrence of an event A can influence the event V or vice versa. To take into account such dependence of some events on others, the concept of conditional probability is introduced.

Definition. If the probability of an event V is located under the condition that the event A happened, then the resulting probability of the event V called conditional probability events V. The following symbols are used to denote such a conditional probability: R A ( V) or R(V / A).

Remark 2. In contrast to the conditional probability, the “unconditional” probability is also considered, when any conditions for the occurrence of some event V missing.

Example. An urn contains 5 balls, 3 of which are red and 2 are blue. In turn, one ball is drawn from it with a return and without a return. Find the conditional probability of drawing a red ball for the second time, provided that the first time taken is: a) a red ball; b) a blue ball.

Let the event A is drawing the red ball for the first time, and the event V– extracting the red ball for the second time. It's obvious that R(A) = 3 / 5; then in the case when the ball taken out for the first time is returned to the urn, R(V)=3/5. In the case when the drawn ball is not returned, the probability of drawing a red ball R(V) depends on which ball was drawn for the first time - red (event A) or blue (event). Then in the first case R A ( V) = 2 / 4, and in the second ( V) = 3 / 4.

The theorem of multiplication of the probabilities of events, one of which takes place under the condition of the other

The probability of the product of two events is equal to the product of the probability of one of them by the conditional probability of the other, found under the assumption that the first event occurred:

R(A ∙ B) = R(A) ∙ R A ( V) . (1.7)

Proof. Indeed, let n – total number equally possible and incompatible (elementary) test outcomes. Let it go n 1 - the number of outcomes that favor the event A, which occurs at the beginning, and m- the number of outcomes in which the event occurs V assuming that the event A has come. In this way, m is the number of outcomes that favor the event V. Then we get:

Those. the probability of the product of several events is equal to the product of the probability of one of these events by the conditional probabilities of the others, and the conditional probability of each subsequent event is calculated on the assumption that all previous events have occurred.

Example. There are 4 masters of sports in a team of 10 athletes. By drawing lots, 3 athletes are selected from the team. What is the probability that all the selected athletes are masters of sports?

Solution. Let us reduce the problem to the “urn” model, i.e. Let's assume that there are 4 red balls and 6 white ones in an urn containing 10 balls. 3 balls are drawn at random from this urn (selection S= 3). Let the event A consists in extracting 3 balls. The problem can be solved in two ways: by the classical scheme and by formula (1.9).

The first method based on the combinatorics formula:

The second method (by formula (1.9)). 3 balls are drawn consecutively from the urn without replacement. Let A 1 - the first drawn ball is red, A 2 - the second drawn ball is red, A 3 - the third drawn ball is red. Let also the event A means that all 3 drawn balls are red. Then: A = A 1 ∙ (A 2 / A 1) ∙ A 3 / (A 1 ∙ A 2), i.e.

Example. Let from the set of cards a, a, r, b, o, t cards are drawn one at a time. What is the probability of getting the word " Work” when sequentially folding them into one line from left to right?

Let V- the event at which the declared word is obtained. Then by formula (1.9) we get:

R(V) = 1/6 ∙ 2/5 ∙ 1/4 ∙ 1/3 ∙ 1/2 ∙ 1/1 = 1/360.

The probability multiplication theorem takes on its simplest form when the product is formed by events independent of each other.

Definition. Event V called independent from the event A if its probability does not change regardless of whether the event occurred A or not. Two events are called independent (dependent) if the occurrence of one of them does not change (changes) the probability of occurrence of the other. Thus, for independent events p(B/A) = R(V) or = R(V), and for dependent events R(V/A)

There will also be tasks for independent decision to which you can see the answers.

General statement of the problem: the probabilities of some events are known, but the probabilities of other events that are associated with these events need to be calculated. In these problems, there is a need for such operations on probabilities as addition and multiplication of probabilities.

For example, two shots were fired while hunting. Event A- hitting a duck from the first shot, event B- hit from the second shot. Then the sum of events A and B- hit from the first or second shot or from two shots.

Tasks of a different type. Several events are given, for example, a coin is tossed three times. It is required to find the probability that either all three times the coat of arms will fall out, or that the coat of arms will fall out at least once. This is a multiplication problem.

Addition of probabilities of incompatible events

Probability addition is used when it is necessary to calculate the probability of a combination or a logical sum of random events.

Sum of events A and B designate A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B- an event that occurs if and only if an event occurs during the observation A or event B, or at the same time A and B.

If events A and B are mutually inconsistent and their probabilities are given, the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.

The theorem of addition of probabilities. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:

For example, two shots were fired while hunting. Event A– hitting a duck from the first shot, event V– hit from the second shot, event ( A+ V) - hit from the first or second shot or from two shots. So if two events A and V are incompatible events, then A+ V- the occurrence of at least one of these events or two events.

Example 1 A box contains 30 balls of the same size: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball is taken without looking.

Solution. Let's assume that the event A– “the red ball is taken”, and the event V- "The blue ball is taken." Then the event is “a colored (not white) ball is taken”. Find the probability of an event A:

and events V:

Events A and V- mutually incompatible, since if one ball is taken, then balls of different colors cannot be taken. Therefore, we use the addition of probabilities:

The theorem of addition of probabilities for several incompatible events. If the events make up the complete set of events, then the sum of their probabilities is equal to 1:

The sum of the probabilities of opposite events is also equal to 1:

Opposite events form a complete set of events, and the probability of a complete set of events is 1.

The probabilities of opposite events are usually denoted in small letters. p and q. In particular,

from which the following formulas for the probability of opposite events follow:

Example 2 The target in the dash is divided into 3 zones. The probability that a certain shooter will shoot at a target in the first zone is 0.15, in the second zone - 0.23, in the third zone - 0.17. Find the probability that the shooter hits the target and the probability that the shooter misses the target.

Solution: Find the probability that the shooter will hit the target:

Find the probability that the shooter misses the target:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Addition of probabilities of mutually joint events

Two random events are said to be joint if the occurrence of one event does not preclude the occurrence of a second event in the same observation. For example, when throwing a dice, the event A is considered to be the occurrence of the number 4, and the event V- dropping an even number. Since the number 4 is an even number, the two events are compatible. In practice, there are tasks for calculating the probabilities of the occurrence of one of the mutually joint events.

The theorem of addition of probabilities for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events is as follows:

Because the events A and V compatible, event A+ V occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:

Event A occurs if one of two incompatible events occurs: or AB. However, the probability of occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:

Similarly:

Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:

When using formula (8), it should be taken into account that the events A and V may be:

• mutually independent;
• mutually dependent.

Probability formula for mutually independent events:

Probability formula for mutually dependent events:

If events A and V are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is as follows:

Example 3 In auto racing, when driving in the first car, the probability of winning, when driving in the second car. Find:

• the probability that both cars will win;
• the probability that at least one car will win;

1) The probability that the first car will win does not depend on the result of the second car, so the events A(first car wins) and V(second car wins) - independent events. Find the probability that both cars win:

2) Find the probability that one of the two cars will win:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Solve the problem of addition of probabilities yourself, and then look at the solution

Example 4 Two coins are thrown. Event A- loss of coat of arms on the first coin. Event B- loss of coat of arms on the second coin. Find the probability of an event C = A + B .

Probability multiplication

Multiplication of probabilities is used when the probability of a logical product of events is to be calculated.

In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.

Probability multiplication theorem for independent events. The probability of the simultaneous occurrence of two independent events A and V is equal to the product of the probabilities of these events and is calculated by the formula:

Example 5 The coin is tossed three times in a row. Find the probability that the coat of arms will fall out all three times.

Solution. The probability that the coat of arms will fall on the first toss of a coin, the second time, and the third time. Find the probability that the coat of arms will fall out all three times:

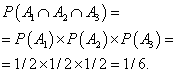
Solve problems for multiplying probabilities yourself, and then look at the solution

Example 6 There is a box with nine new tennis balls. Three balls are taken for the game, after the game they are put back. When choosing balls, they do not distinguish between played and unplayed balls. What is the probability that after three games there will be no unplayed balls in the box?

Example 7 32 letters of the Russian alphabet are written on cut alphabet cards. Five cards are drawn at random, one after the other, and placed on the table in the order in which they appear. Find the probability that the letters will form the word "end".

Example 8 From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards are of the same suit.

Example 9 The same problem as in example 8, but each card is returned to the deck after being drawn.

More complex tasks, in which you need to apply both addition and multiplication of probabilities, as well as calculate the product of several events, on the page "Various tasks for addition and multiplication of probabilities" .

The probability that at least one of the mutually independent events will occur can be calculated by subtracting the product of the probabilities of opposite events from 1, that is, by the formula.