We already know that probability is a numerical measure of the possibility of a random event occurring, i.e. an event that may or may not occur under a certain set of conditions. When the set of conditions changes, the probability of a random event may change. As an additional condition, we can consider the occurrence of another event. So, if the set of conditions under which a random event occurs A, add one more, consisting in the occurrence of a random event V, then the probability of the event occurring A will be called conditional.

Conditional probability of event AThe probability that event A will occur given that event B has occurred. The conditional probability is denoted (A).

Example 16 A box contains 7 white and 5 black balls, differing only in color. The experiment consists in the fact that one ball is randomly taken out and, without lowering it back, another ball is taken out. What is the probability that the second ball drawn is black if the first ball drawn is white?

Solution.

We have two random events: the event A- the first ball drawn is white, V– the second drawn ball is black. A and B are incompatible events, let's use the classical definition of probability. The number of elementary outcomes when drawing the first ball is 12, and the number of favorable outcomes to get the white ball is 7. Therefore, the probability P(A) = 7/12.

If the first ball is white, then the conditional probability of the event V- the appearance of the second black ball (assuming that the first ball was white) is equal to (V)= 5/11, since there are 11 balls left before the second ball is taken out, of which 5 are black.

Note that the probability of a black ball appearing on the second drawing would not depend on the color of the first ball drawn if, having taken the first ball, we put it back into the box.

Consider two random events A and B. Let the probabilities P(A) and (B) be known. Let us determine what the probability of occurrence of both event A and event B is, i.e. products of these events.

Probability multiplication theorem. The probability of the product of two events is equal to the product of the probability of one of them by the conditional probability of the other, calculated under the condition that the first event occurred:

P (A × B) \u003d P (A) × (B) .

Since for calculating the probability of a product it does not matter which of the considered events A and V was the first, and which was the second, then you can write:

P(A×B) = P(A) × (B) = P(B) × (A).

The theorem can be extended to the product of n events:

P (A 1 A 2. A p) \u003d P (A x) P (A 2 / A 1) .. P (A p / A 1 A 2 ... A p-1).

Example 17. For the conditions of the previous example, calculate the probability of drawing two balls: a) a white ball first, and a black ball second; b) two black balls.

Solution.

a) From the previous example, we know the probabilities of drawing a white ball first and a black ball second from the box, provided that the white ball was taken first. To calculate the probability of both events occurring together, we use the probabilities multiplication theorem: P (A × B) \u003d P (A) × (B) \u003d .

b) Similarly, we calculate the probability of drawing two black balls. Probability of getting the black ball first . Probability of drawing a black ball a second time, provided that we do not put the first black ball drawn back into the box (there are 4 black balls left, and the total number of balls is 11). The resulting probability can be calculated using the formula P (A × B) \u003d P (A) × (B) 0,152.

The probability multiplication theorem has a simpler form if the events A and B are independent.

An event B is said to be independent of event A if the probability of event B does not change whether event A occurs or not. If event B is independent of event A, then its conditional (B) is equal to the usual probability P(B):

It turns out that if the event V will be event independent A, then the event A will be independent of V, i.e. (A)=P(A).

Let's prove it. Substitute the equality from the definition of event independence V from the event A into the probability multiplication theorem: P (A × B) \u003d P (A) × (B) \u003d P (A) × (B). But in other way P(A×B)= P(B) × (A). Means P(A) × (B)= P(B) × (A) and (A)=P(A).

Thus, the property of independence (or dependence) of events is always mutual and can be given the following definition: two events are called independent if the occurrence of one of them does not change the probability of occurrence of the other.

It should be noted that the independence of events is based on the independence of the physical nature of their origin. This means that the sets of random factors leading to one or another outcome of testing one and another random event are different. So, for example, hitting a target by one shooter does not affect in any way (unless, of course, you come up with any exotic reasons) the probability of hitting the target by a second shooter. In practice, independent events occur very often, since causality phenomena in many cases is absent or insignificant.

Probability multiplication theorem for independent events. The probability of the product of two independent events is equal to the product of the probabilities of these events: P(A×B) = P(A) × P(B).

The following corollary follows from the probability multiplication theorem for independent events.

If events A and B are incompatible and P(A)¹0, P(B)¹0, then they are dependent.

Let us prove this by contradiction. Let us assume that incompatible events A and V independent. Then P(A×B) = P(A)×P(B). And since P(A)¹0, P(B)¹0, i.e. events A and V are not impossible, then P(A×B)¹0. But, on the other hand, the event Až V is impossible as a work of joint events(this was discussed above). Means P(A×B)=0. got a contradiction. Thus, our initial assumption is incorrect. Events A and V- dependent.

Example 18. Let us now return to the unsolved problem of two shooters shooting at the same target. Recall that if the probability of hitting the target by the first shooter is 0.8, and the second is 0.7, it is necessary to find the probability of hitting the target.

Events A and V- hitting the target, respectively, by the first and second shooters - joint, therefore, to find the probability of the sum of events A + V- hitting a target by at least one shooter - you must use the formula: P(A+B) \u003d P (A) + P (B)–P(Až V). Events A and V independent, therefore P(A × B) = P(A) × P(B).

So, P(A+B) \u003d P (A) + P (B) - P(A) × P(B).

P(A+B)= 0.8 + 0.7 - 0.8 × 0.7 = 0.94.

Example 19.

Two independent shots are fired at the same target. The probability of hitting with the first shot is 0.6, and with the second - 0.8. Find the probability of hitting the target with two shots.

1) Denote the hit on the first shot as an event
A 1 , with the second - as an event A 2 .

Hitting the target involves at least one hit: either only on the first shot, or only on the second, or both on the first and on the second. Therefore, in the problem it is required to determine the probability of the sum of two joint events A 1 and A 2:

P (A 1 + A 2) \u003d P (A 1) + P (A 2) -P (A 1 A 2).

2) Since the events are independent, then P (A 1 A 2) \u003d P (A 1) P (A 2).

3) We get: P (A 1 + A 2) \u003d 0.6 + 0.8 - 0.6 0.8 \u003d 0.92.
If the events are incompatible, then P(A B) = 0 and P(A + B) = P(A) + P(B).

Example 20.

An urn contains 2 white, 3 red and 5 blue balls of the same size. What is the probability that a ball drawn at random from the urn will be colored (not white)?

1) Let the event A be the extraction of a red ball from the urn,
event B - extraction of the blue ball. Then the event (A + B)
is the extraction of a colored ball from the urn.

2) P(A) = 3/10, P(B) = 5/10.

3) Events A and B are incompatible, since only
one ball. Then: P(A + B) = P(A) + P(B) = 0.3 + 0.5 = 0.8.

Example 21.

An urn contains 7 white and 3 black balls. What is the probability of: 1) drawing a white ball from the urn (event A); 2) drawing a white ball from the urn after removing one white ball from it (event B); 3) extracting a white ball from the urn after removing one ball from it, which is black (event C)?

1) Р(А) = = 0.7 (see classical probability).

2) P B (A) = = 0, (6).

3) P C (A) = | = 0,(7).

Example 22.

The mechanism is assembled from three identical parts and is considered inoperable if all three parts are out of order. There are 15 parts left in the assembly shop, of which 5 are non-standard (defective). What is the probability that the mechanism assembled from the remaining parts taken at random will be inoperable?

1) Denote the desired event through A, the choice of the first non-standard part through A 1, the second through A 2, the third through A 3

2) Event A will occur if both event A 1 and event A 2 and event A 3 occur, i.e.

A \u003d A 1 A 2 A 3,

since the logical "and" corresponds to the product (see section "Propositional Algebra. Logical Operations").

3) Events A 1, A 2, A 3 are dependent, therefore P (A 1 A 2 A 3) =
\u003d P (A 1) P (A 2 / A 1) P (A 3 / A 1 A 2).

4) P (A 1) \u003d, P (A 2 / A 1) \u003d, P (A 3 / A 1 A 2) \u003d. Then

P (A 1 A 2 A 3) \u003d 0.022.

For independent events: P(A B) = P(A) P(B).

Based on the above, the criterion for the independence of two events A and B:

P (A) \u003d P B (A) \u003d P (A), P (B) \u003d P A (B) \u003d P (B).

Example 23.

The probability of hitting the target by the first shooter (event A) is 0.9, and the probability of hitting the target by the second shooter (event B) is 0.8. What is the probability that the target will be hit by at least one shooter?

1) Let C be the event of interest to us; the opposite event is that both arrows missed.

3) Since when shooting one shooter does not interfere with the other, the events and are independent.

We have: Р() = Р() Р() = =(1 - 0.9) (1 - 0.8) =

0,1 0,2 = 0,02.

4) P(C) = 1 -P() = 1 -0.02 = 0.98.

Formula full probability

Let the event A can occur as a result of the manifestation of one and only one event Н i (i = 1,2,... n) from some complete group of incompatible events H 1 , H 2,… H n . The events of this group are usually called hypotheses.

Total Probability Formula. The probability of an event A is equal to the sum of the paired products of the probabilities of all hypotheses that form a complete group and the corresponding conditional probabilities of this event A:

P(A) = , where = 1.

Example 24.

There are 3 identical urns. The first urn contains 2 white and 1 black balls, the second urn contains 3 white and 1 black ball, and the third urn contains 2 white and 2 black balls. 1 ball is selected from an urn chosen at random. What is the probability that he will be white?

All urns are considered the same, therefore, the probability of choosing the i-th urn is

Р(H i) = 1/3, where i = 1, 2, 3.

2) Probability of drawing a white ball from the first urn: (A) = .

Probability of drawing a white ball from the second urn: (A) = .

Probability of drawing a white ball from the third urn: (A) = .

3) The desired probability:

P(A) = =0.63(8)

Example 25.

The store receives for sale the products of three factories, the relative shares of which are: I - 50%, II - 30%, III - 20%. For the products of factories, the marriage is respectively: I - 2%, P - 2%, III - 5%. What is the probability that a product of this product, randomly purchased in a store, will be of good quality (event A)?

1) The following three hypotheses are possible here: H 1 , H 2, H 3 -
the purchased item was worked out, respectively, at factories I, II, III; the system of these hypotheses is complete.

Probabilities: P(H 1) = 0.5; P (H 2) \u003d 0.3; P (H 3) \u003d 0.2.

2) The corresponding conditional probabilities of event A are: (A) = 1-0.02 = 0.98; (A)=1-0.03=0.97; (A) == 1-0.05 = 0.95.

3) According to the total probability formula, we have: P (A) \u003d 0.5 0.98 + + 0.3 0.97 + 0.2 0.95 \u003d 0.971.

Posterior probability formula (Bayes formula)

Consider the situation.

There is a complete group of inconsistent hypotheses H 1 , H 2, … H n , whose probabilities (i = 1, 2, ... n) are known before experiment (a priori probabilities). An experiment (test) is carried out, as a result of which the occurrence of event A is registered, and it is known that our hypotheses attributed certain probabilities to this event (i = 1, 2, ... n). What will be the probabilities of these hypotheses after the experiment (a posteriori probabilities)?

The answer to a similar question is given by the posterior probability formula (Bayes formula):

, where i=1,2, ...p.

Example 26.

The probability of hitting an aircraft in a single shot for the 1st missile system (event A) is 0.2, and for the 2nd (event B) - 0.1. Each of the complexes fires one shot, and one hit on the aircraft is registered (event C). What is the probability that the successful shot belongs to the first missile system?

Solution.

1) Before the experiment, four hypotheses are possible:

H 1 \u003d A B - the aircraft is hit by the 1st complex and the aircraft is hit by the 2nd complex (the product corresponds to the logical "and"),

H 2 \u003d A B - the aircraft was hit by the 1st complex and the aircraft was not hit by the 2nd complex,

H 3 \u003d A B - the aircraft is not affected by the 1st complex and the aircraft is affected by the 2nd complex,

H 4 = A B - the aircraft is not affected by the 1st complex and the aircraft is not affected by the 2nd complex.

These hypotheses form a complete group of events.

2) Corresponding probabilities (with independent action of complexes):

P (H 1) \u003d 0.2 0.1 \u003d 0.02;

P(H 2) = 0.2 (1-0.1) = 0.18;

P (H 3) \u003d (1-0.2) 0.1 \u003d 0.08;

P (H 4) \u003d (1-0.2) (1-0.1) \u003d 0.72.

3) Since the hypotheses form a complete group of events, the equality = 1 must hold.

We check: P (H 1) + P (H 2) + P (H 3) + P (H 4) \u003d 0.02 + 0.18 + + 0.08 + 0.72 \u003d 1, thus, the group under consideration hypotheses is correct.

4) Conditional probabilities for the observed event C under these hypotheses will be: (C) = 0, since according to the condition of the problem one hit was registered, and the hypothesis H 1 assumes two hits:

(C)=1; (C) = 1.

(C) = 0, since according to the condition of the problem, one hit was registered, and the hypothesis H 4 assumes the absence of hits. Therefore, the hypotheses H 1 and H 4 are dropped.

5) The probabilities of hypotheses H 2 and H 3 are calculated using the Bayes formula:

0,7, 0,3.

Thus, with a probability of approximately 70% (0.7), it can be argued that a successful shot belongs to the first missile system.

5.4. random variables. Distribution law of a discrete random variable

Quite often, in practice, such tests are considered, as a result of which a certain number is randomly obtained. For example, when throwing a dice, a number of points from 1 to 6 falls out, when taking 6 cards from a deck, you can get from 0 to 4 aces. For a certain period of time (say, a day or a month), a certain number of crimes are registered in the city, a certain number of traffic accidents occur. A shot is fired from the gun. The range of the projectile also takes on a random value.

In all these tests, we are faced with the so-called random variables.

A numerical value that takes on a particular value as a result of the implementation of the test in a random way is called random variable.

The concept of a random variable plays a very important role in probability theory. If the "classical" probability theory studied mainly random events, then modern probability theory mainly deals with random variables.

Further, we will denote random variables by uppercase Latin letters X, Y, Z, etc., and their possible values ​​by the corresponding lowercase x, y, z. For example, if random value has three possible values, we will denote them as follows: , , .

So, examples of random variables can be:

1) the number of points rolled on the top face of the dice:

2) the number of aces, when taking 6 cards from a deck;

3) the number of registered crimes per day or month;

4) the number of hits on the target with four pistol shots;

5) the distance that the projectile will fly when fired from the gun;

6) the height of a randomly taken person.

It can be seen that in the first example, the random variable can take one of six possible values: 1, 2, 3, 4, 5, and 6. In the second and fourth examples, the number of possible values ​​of the random variable is five: 0, 1, 2, 3, 4 In the third example, the value of a random variable can be any (theoretically) natural number or 0. In the fifth and sixth examples, the random variable can take on any real value from a certain interval ( a, b).

If a random variable can take on a finite or countable set of values, then it is called discrete(discretely distributed).

continuous A random variable is such a random variable that can take on all values ​​from some finite or infinite interval.

To specify a random variable, it is not enough to list its possible values. For example, in the second and third examples, random variables could take the same values: 0, 1, 2, 3, and 4. However, the probabilities with which these random variables take their values ​​will be completely different. Therefore, to specify a discrete random variable, in addition to the list of all its possible values, one must also indicate their probabilities.

The correspondence between the possible values ​​of a random variable and their probabilities is called distribution law discrete random variable. , …, Х=

The distribution polygon, as well as the distribution series, completely characterizes the random variable. It is one of the forms of the law of distribution.

Example 27. A coin is tossed randomly. Construct a row and a polygon for the distribution of the number of coats of arms that have fallen.

A random value equal to the number of coats of arms that fell out can take two values: 0 and 1. The value 1 corresponds to the event - the loss of the coat of arms, the value 0 - the loss of tails. The probabilities of getting a coat of arms and getting tails are the same and equal. Those. the probabilities with which the random variable takes the values ​​0 and 1 are equal. The distribution series has the form:

X
p

The sum of all event probabilities in the sample space is 1. For example, if the experiment is a coin toss with Event A = "heads" and Event B = "tails", then A and B represent the entire sample space. Means, P(A) + P(B) = 0.5 + 0.5 = 1.

Example. In the previously proposed example of calculating the probability of extracting a red pen from the pocket of a bathrobe (this is event A), in which there are two blue and one red pen, P(A) = 1/3 ≈ 0.33, the probability of the opposite event - extracting a blue pen - will be

Before proceeding to the main theorems, we introduce two more more complex concepts - the sum and the product of events. These concepts are different from the usual concepts of sum and product in arithmetic. Addition and multiplication in probability theory are symbolic operations subject to certain rules and facilitating the logical construction of scientific conclusions.

sum of several events is an event consisting in the occurrence of at least one of them. That is, the sum of two events A and B is called event C, which consists in the appearance of either event A, or event B, or events A and B together.

For example, if a passenger is waiting at a tram stop for one of the two routes, then the event he needs is the appearance of a tram of the first route (event A), or a tram of the second route (event B), or a joint appearance of trams of the first and second routes (event WITH). In the language of probability theory, this means that the event D that the passenger needs is the appearance of either event A, or event B, or event C, which can be symbolically written as:

D=A+B+C

The product of two eventsA and V is an event consisting in the joint occurrence of events A and V. The product of several events the joint occurrence of all these events is called.

In the passenger example above, the event WITH(joint appearance of trams of two routes) is a product of two events A and V, which is symbolically written as follows:

Assume that two physicians are separately examining a patient in order to identify a specific disease. During inspections, the following events may occur:

Detection of diseases by the first physician ( A);

Failure to detect the disease by the first doctor ();

Detection of the disease by the second doctor ( V);

Non-detection of the disease by the second doctor ().

Consider the event that the disease is detected exactly once during the examinations. This event can be implemented in two ways:

The disease is detected by the first doctor ( A) and will not find the second ();

Diseases will not be detected by the first doctor () and will be detected by the second ( B).

Let us denote the event under consideration by and write it symbolically:

Consider the event that the disease is discovered in the process of examinations twice (both by the first and the second doctor). Let's denote this event by and write: .

The event, which consists in the fact that neither the first nor the second doctor detects the disease, will be denoted by and we will write: .

Basic theorems of probability theory

The probability of the sum of two incompatible events is equal to the sum of the probabilities of these events.

Let's write the addition theorem symbolically:

P(A + B) = P(A) + P(B),

where R- the probability of the corresponding event (the event is indicated in brackets).

Example . The patient has stomach bleeding. This symptom is recorded in ulcerative vessel erosion (event A), rupture of varicose veins of the esophagus (event B), stomach cancer (event C), gastric polyp (event D), hemorrhagic diathesis (event F), obstructive jaundice (event E) and end gastritis (eventG).

The doctor, based on the analysis of statistical data, assigns a probability value to each event:

In total, the doctor had 80 patients with gastric bleeding (n= 80), of which 12 had ulcerative vessel erosion (), at6 - rupture of varicose veins of the esophagus (), 36 had stomach cancer () etc.

To prescribe an examination, the doctor wants to determine the likelihood that stomach bleeding is associated with stomach disease (event I):

The likelihood that gastric bleeding is associated with stomach disease is quite high, and the doctor can determine the tactics of examination based on the assumption of stomach disease, justified at a quantitative level using probability theory.

If joint events are considered, the probability of the sum of two events is equal to the sum of the probabilities of these events without the probability of their joint occurrence.

Symbolically, this is written as follows:

If we imagine that the event A consists in hitting a target shaded with horizontal stripes while shooting, and the event V- in hitting a target shaded with vertical stripes, then in the case of incompatible events, according to the addition theorem, the probability of the sum is equal to the sum of the probabilities of individual events. If these events are joint, then there is some probability corresponding to the joint occurrence of events A and V. If you do not introduce a correction for the deductible P(AB), i.e. on the probability of the joint occurrence of events, then this probability will be taken into account twice, since the area shaded by both horizontal and vertical lines is an integral part of both targets and will be taken into account both in the first and in the second summand.

On fig. 1 a geometric interpretation is given that clearly illustrates this circumstance. In the upper part of the figure there are non-intersecting targets, which are an analogue of incompatible events, in the lower part - intersecting targets, which are an analogue of joint events (one shot can hit both target A and target B at once).

Before proceeding to the multiplication theorem, it is necessary to consider the concepts of independent and dependent events and conditional and unconditional probabilities.

Independent an event B is an event A whose probability of occurrence does not depend on the occurrence or non-occurrence of event B.

addicted An event B is an event A whose probability of occurrence depends on the occurrence or non-occurrence of event B.

Example . An urn contains 3 balls, 2 white and 1 black. When choosing a ball at random, the probability of choosing a white ball (event A) is: P(A) = 2/3, and black (event B) P(B) = 1/3. We are dealing with a scheme of cases, and the probabilities of events are calculated strictly according to the formula. When the experiment is repeated, the probabilities of occurrence of events A and B remain unchanged if after each choice the ball is returned to the urn. In this case, events A and B are independent. If the ball chosen in the first experiment is not returned to the urn, then the probability of the event (A) in the second experiment depends on the occurrence or non-occurrence of the event (B) in the first experiment. So, if event B appeared in the first experiment (a black ball was chosen), then the second experiment is carried out if there are 2 white balls in the urn and the probability of the occurrence of event A in the second experiment is: P(A) = 2/2= 1.

If the event B did not appear in the first experiment (a white ball is chosen), then the second experiment is carried out if there are one white and one black balls in the urn and the probability of the occurrence of event A in the second experiment is equal to: P(A) = 1/2. Obviously, in this case, events A and B are closely related and the probabilities of their occurrence are dependent.

Conditional Probability event A is the probability of its occurrence, provided that event B has appeared. The conditional probability is symbolically denoted P(A/B).

If the probability of an event occurring A does not depend on the occurrence of the event V, then the conditional probability of the event A is equal to the unconditional probability:

If the probability of occurrence of event A depends on the occurrence of event B, then the conditional probability can never be equal to the unconditional probability:

Identification of the dependence of various events among themselves has great importance in solving practical problems. So, for example, an erroneous assumption about the independence of the appearance of certain symptoms in the diagnosis of heart defects using a probabilistic method developed at the Institute of Cardiovascular Surgery. A. N. Bakuleva, caused about 50% of erroneous diagnoses.

When assessing the probability of the occurrence of any random event, it is very important to have a good idea in advance whether the probability (probability of the event) of the occurrence of the event of interest to us depends on how other events develop. In the case of the classical scheme, when all outcomes are equally probable, we can already estimate the probability values ​​of the individual event of interest to us on our own. We can do this even if the event is a complex set several elementary outcomes. And if several random events occur simultaneously or sequentially? How does this affect the probability of the event of interest to us? If I roll a die a few times and want to get a six and I'm not lucky all the time, does that mean I should increase my bet because, according to probability theory, I'm about to get lucky? Alas, probability theory says nothing of the sort. Neither dice, nor cards, nor coins can remember what they showed us last time. It does not matter to them at all whether for the first time or for the tenth time today I test my fate. Every time I roll again, I know only one thing: and this time the probability of rolling a "six" again is one-sixth. Of course, this does not mean that the number I need will never fall out. It only means that my loss after the first toss and after any other toss are independent events. Events A and B are called independent if the realization of one of them does not affect the probability of the other event in any way. For example, the probabilities of hitting a target with the first of two guns do not depend on whether the other gun hit the target, so the events "the first gun hit the target" and "the second gun hit the target" are independent. If two events A and B are independent, and the probability of each of them is known, then the probability of the simultaneous occurrence of both event A and event B (denoted by AB) can be calculated using the following theorem.

Probability multiplication theorem for independent events

P(AB) = P(A)*P(B) the probability of the simultaneous occurrence of two independent events is equal to the product of the probabilities of these events.

Example 1. The probabilities of hitting the target when firing the first and second guns are respectively equal: p 1 = 0.7; p2 = 0.8. Find the probability of hitting with one volley by both guns simultaneously.

As we have already seen, the events A (hit by the first gun) and B (hit by the second gun) are independent, i.e. P(AB)=P(A)*P(B)=p1*p2=0.56. What happens to our estimates if the initiating events are not independent? Let's change the previous example a little.

Example 2 Two shooters in a competition shoot at targets, and if one of them shoots accurately, then the opponent starts to get nervous, and his results worsen. How to turn this worldly situation into math problem and outline ways to solve it? It is intuitively clear that it is necessary to somehow separate the two scenarios, to compose, in fact, two scenarios, two different tasks. In the first case, if the opponent misses, the scenario will be favorable for the nervous athlete and his accuracy will be higher. In the second case, if the opponent decently realized his chance, the probability of hitting the target for the second athlete is reduced. To separate the possible scenarios (they are often called hypotheses) of the development of events, we will often use the "probability tree" scheme. This diagram is similar in meaning to the decision tree, which you have probably already had to deal with. Each branch is a separate scenario for the development of events, only now it has eigenvalue the so-called conditional probability (q 1 , q 2 , q 1 -1, q 2 -1).

This scheme is very convenient for the analysis of successive random events. It remains to clarify one more important question: where do the initial values ​​of probabilities come from in real situations? After all, the theory of probability does not work with the same coins and dice, does it? Usually these estimates are taken from statistics, and when statistics are not available, we conduct our own research. And we often have to start it not with collecting data, but with the question of what information we generally need.

Example 3 In a city of 100,000 inhabitants, suppose we need to estimate the size of the market for a new non-essential product, such as a color-treated hair conditioner. Let's consider the "tree of probabilities" scheme. In this case, we need to approximately estimate the value of the probability on each "branch". So, our estimates of market capacity:

1) 50% of all residents of the city are women,

2) of all women, only 30% dye their hair often,

3) of these, only 10% use balms for colored hair,

4) of these, only 10% can muster up the courage to try a new product,

5) 70% of them usually buy everything not from us, but from our competitors.

According to the law of multiplication of probabilities, we determine the probability of the event of interest to us A \u003d (a city resident buys this new balm from us) \u003d 0.00045. Multiply this probability value by the number of inhabitants of the city. As a result, we have only 45 potential buyers, and given that one vial of this product is enough for several months, the trade is not very lively. Still, there are benefits from our assessments. Firstly, we can compare the forecasts of different business ideas, they will have different “forks” on the diagrams, and, of course, the probability values ​​will also be different. Secondly, as we have already said, a random variable is not called random because it does not depend on anything at all. It's just that its exact meaning is not known in advance. We know that the average number of buyers can be increased (for example, by advertising a new product). So it makes sense to focus on those "forks" where the distribution of probabilities does not particularly suit us, on those factors that we are able to influence. Consider another quantitative example of consumer behavior research.

Example 3 An average of 10,000 people visit the food market per day. The probability that a market visitor walks into a dairy pavilion is 1/2. It is known that in this pavilion, on average, 500 kg of various products are sold per day. Can it be argued that the average purchase in the pavilion weighs only 100 g?

Discussion.

Of course not. It is clear that not everyone who entered the pavilion ended up buying something there.

As shown in the diagram, in order to answer the question about the average purchase weight, we must find the answer to the question, what is the probability that a person who enters the pavilion buys something there. If we do not have such data at our disposal, but we need them, we will have to obtain them ourselves, after observing the visitors of the pavilion for some time. Suppose our observations show that only a fifth of the visitors to the pavilion buy something. As soon as these estimates are obtained by us, the task becomes already simple. Of the 10,000 people who came to the market, 5,000 will go to the pavilion of dairy products, there will be only 1,000 purchases. The average purchase weight is 500 grams. It is interesting to note that in order to build a complete picture of what is happening, the logic of conditional "branching" must be defined at each stage of our reasoning as clearly as if we were working with a "concrete" situation, and not with probabilities.

Tasks for self-examination.

1. Let it eat electrical circuit, consisting of n series-connected elements, each of which works independently of the others. The probability p of non-failure of each element is known. Determine the probability of proper operation of the entire section of the circuit (event A).

2. The student knows 20 of the 25 exam questions. Find the probability that the student knows the three questions given to him by the examiner.

3. Production consists of four successive stages, each of which operates equipment for which the probabilities of failure within the next month are, respectively, p 1 , p 2 , p 3 and p 4 . Find the probability that in a month there will be no stoppage of production due to equipment failure.

There will also be tasks for independent solution to which you can see the answers.

General statement of the problem: the probabilities of some events are known, but the probabilities of other events that are associated with these events need to be calculated. In these problems, there is a need for such operations on probabilities as addition and multiplication of probabilities.

For example, two shots were fired while hunting. Event A- hitting a duck from the first shot, event B- hit from the second shot. Then the sum of events A and B- hit from the first or second shot or from two shots.

Tasks of a different type. Several events are given, for example, a coin is tossed three times. It is required to find the probability that either all three times the coat of arms will fall out, or that the coat of arms will fall out at least once. This is a multiplication problem.

Addition of probabilities of incompatible events

Probability addition is used when it is necessary to calculate the probability of a combination or a logical sum of random events.

Sum of events A and B designate A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B- an event that occurs if and only if an event occurs during the observation A or event B, or at the same time A and B.

If events A and B are mutually inconsistent and their probabilities are given, the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.

The theorem of addition of probabilities. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:

For example, two shots were fired while hunting. Event A– hitting a duck from the first shot, event V– hit from the second shot, event ( A+ V) - hit from the first or second shot or from two shots. So if two events A and V are incompatible events, then A+ V- the occurrence of at least one of these events or two events.

Example 1 A box contains 30 balls of the same size: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball is taken without looking.

Solution. Let's assume that the event A– “the red ball is taken”, and the event V- "The blue ball is taken." Then the event is “a colored (not white) ball is taken”. Find the probability of an event A:

and events V:

Events A and V- mutually incompatible, since if one ball is taken, then balls of different colors cannot be taken. Therefore, we use the addition of probabilities:

The theorem of addition of probabilities for several incompatible events. If the events make up the complete set of events, then the sum of their probabilities is equal to 1:

The sum of the probabilities of opposite events is also equal to 1:

Opposite events form a complete set of events, and the probability of a complete set of events is 1.

The probabilities of opposite events are usually denoted in small letters. p and q. In particular,

from which the following formulas for the probability of opposite events follow:

Example 2 The target in the dash is divided into 3 zones. The probability that a certain shooter will shoot at a target in the first zone is 0.15, in the second zone - 0.23, in the third zone - 0.17. Find the probability that the shooter hits the target and the probability that the shooter misses the target.

Solution: Find the probability that the shooter hits the target:

Find the probability that the shooter misses the target:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Addition of probabilities of mutually joint events

Two random events are said to be joint if the occurrence of one event does not preclude the occurrence of a second event in the same observation. For example, when throwing a dice, the event A is considered to be the occurrence of the number 4, and the event V- dropping an even number. Since the number 4 is an even number, the two events are compatible. In practice, there are tasks for calculating the probabilities of the occurrence of one of the mutually joint events.

The theorem of addition of probabilities for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events is as follows:

Because the events A and V compatible, event A+ V occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:

Event A occurs if one of two incompatible events occurs: or AB. However, the probability of occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:

Similarly:

Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:

When using formula (8), it should be taken into account that the events A and V may be:

• mutually independent;
• mutually dependent.

Probability formula for mutually independent events:

Probability formula for mutually dependent events:

If events A and V are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is as follows:

Example 3 In auto racing, when driving in the first car, the probability of winning, when driving in the second car. Find:

• the probability that both cars will win;
• the probability that at least one car will win;

1) The probability that the first car will win does not depend on the result of the second car, so the events A(first car wins) and V(second car wins) - independent events. Find the probability that both cars win:

2) Find the probability that one of the two cars will win:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Solve the problem of addition of probabilities yourself, and then look at the solution

Example 4 Two coins are thrown. Event A- loss of coat of arms on the first coin. Event B- loss of coat of arms on the second coin. Find the probability of an event C = A + B .

Probability multiplication

Multiplication of probabilities is used when the probability of a logical product of events is to be calculated.

In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.

Probability multiplication theorem for independent events. The probability of the simultaneous occurrence of two independent events A and V is equal to the product of the probabilities of these events and is calculated by the formula:

Example 5 The coin is tossed three times in a row. Find the probability that the coat of arms will fall out all three times.

Solution. The probability that the coat of arms will fall on the first toss of a coin, the second time, and the third time. Find the probability that the coat of arms will fall out all three times:

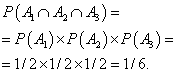
Solve problems for multiplying probabilities yourself, and then look at the solution

Example 6 There is a box with nine new tennis balls. Three balls are taken for the game, after the game they are put back. When choosing balls, they do not distinguish between played and unplayed balls. What is the probability that after three games there will be no unplayed balls in the box?

Example 7 32 letters of the Russian alphabet are written on cut alphabet cards. Five cards are drawn at random, one after the other, and placed on the table in the order in which they appear. Find the probability that the letters will form the word "end".

Example 8 From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards are of the same suit.

Example 9 The same problem as in example 8, but each card is returned to the deck after being drawn.

More complex tasks, in which you need to apply both addition and multiplication of probabilities, as well as calculate the product of several events, on the page "Various tasks for addition and multiplication of probabilities" .

The probability that at least one of the mutually independent events will occur can be calculated by subtracting the product of the probabilities of opposite events from 1, that is, by the formula.

Theorems of addition and multiplication of probabilities.
Dependent and independent events

The title looks scary, but it's actually very simple. In this lesson, we will get acquainted with the theorems of addition and multiplication of the probabilities of events, and also analyze typical tasks, which, along with task for the classical definition of probability will definitely meet or, more likely, have already met on your way. To effectively study the materials of this article, you need to know and understand the basic terms probability theory and be able to perform simple arithmetic operations. As you can see, very little is required, and therefore a fat plus in the asset is almost guaranteed. But on the other hand, I again warn against a superficial attitude to practical examples - there are also enough subtleties. Good luck:

The addition theorem for the probabilities of incompatible events: the probability of occurrence of one of the two incompatible events or (no matter what), is equal to the sum of the probabilities of these events:

A similar fact is also true for a larger number of incompatible events, for example, for three incompatible events and :

Dream theorem =) However, such a dream is also subject to proof, which can be found, for example, in study guide V.E. Gmurman.

Let's get acquainted with new, hitherto unseen concepts:

Dependent and independent events

Let's start with independent events. Events are independent if the probability of occurrence any of them does not depend from the appearance/non-appearance of other events of the considered set (in all possible combinations). ... But what is there to grind out common phrases:

The theorem of multiplication of probabilities of independent events: the probability of joint occurrence of independent events and is equal to the product of the probabilities of these events:

Let's return to the simplest example of the 1st lesson, in which two coins are tossed and the following events:

- heads will fall on the 1st coin;
- Heads on the 2nd coin.

Let's find the probability of the event (heads will appear on the 1st coin and Eagle will appear on the 2nd coin - remember how to read product of events!) . The probability of getting heads on one coin does not depend on the result of tossing another coin, therefore, the events and are independent.

Similarly:
is the probability that the 1st coin will land heads and on the 2nd tail;
is the probability that heads appear on the 1st coin and on the 2nd tail;
is the probability that the 1st coin will land on tails and on the 2nd eagle.

Note that events form full group and the sum of their probabilities is equal to one: .

The multiplication theorem obviously extends to a larger number of independent events, so, for example, if the events are independent, then the probability of their joint occurrence is: . Let's practice on concrete examples:

Task 3

Each of the three boxes contains 10 parts. In the first box there are 8 standard parts, in the second - 7, in the third - 9. One part is randomly removed from each box. Find the probability that all parts are standard.

Solution: the probability of extracting a standard or non-standard part from any box does not depend on which parts will be extracted from other boxes, so the problem is about independent events. Consider the following independent events:

– a standard part is removed from the 1st box;
– a standard part is removed from the 2nd box;
– A standard part has been removed from the 3rd drawer.

According to the classical definition:
are the corresponding probabilities.

Event we are interested in (Standard part will be taken from the 1st drawer and from the 2nd standard and from the 3rd standard) is expressed by the product.

According to the theorem of multiplication of probabilities of independent events:

is the probability that one standard part will be extracted from three boxes.

Answer: 0,504

After invigorating exercises with boxes, no less interesting urns await us:

Task 4

Three urns contain 6 white and 4 black balls. One ball is drawn at random from each urn. Find the probability that: a) all three balls will be white; b) all three balls will be the same color.

Based on the information received, guess how to deal with the “be” item ;-) An approximate sample solution is designed in an academic style with a detailed description of all events.

Dependent events. The event is called dependent if its probability depends from one or more events that have already happened. You don’t have to go far for examples - just go to the nearest store:

- Tomorrow at 19.00 fresh bread will be on sale.

The probability of this event depends on many other events: whether fresh bread will be delivered tomorrow, whether it will be sold out before 7 pm or not, etc. Depending on various circumstances, this event can be both reliable and impossible. So the event is dependent.

Bread ... and, as the Romans demanded, circuses:

- at the exam, the student will get a simple ticket.

If you go not the very first, then the event will be dependent, since its probability will depend on which tickets the classmates have already drawn.

How to determine dependency/independence of events?

Sometimes this is directly stated in the condition of the problem, but most often you have to conduct an independent analysis. There is no unambiguous guideline here, and the fact of dependence or independence of events follows from natural logical reasoning.

In order not to throw everything in one heap, tasks for dependent events I will highlight the next lesson, but for now we will consider the most common bunch of theorems in practice:

Problems on addition theorems for inconsistent probabilities
and multiplying the probabilities of independent events

This tandem, according to my subjective assessment, works in about 80% of the tasks on the topic under consideration. A hit of hits and a real classic of probability theory:

Task 5

Two shooters fired one shot each at the target. The probability of hitting for the first shooter is 0.8, for the second - 0.6. Find the probability that:

a) only one shooter will hit the target;
b) at least one of the shooters will hit the target.

Solution: The hit/miss probability of one shooter is obviously independent of the other shooter's performance.

Consider the events:
– 1st shooter will hit the target;
– The 2nd shooter will hit the target.

By condition: .

Let's find the probabilities of opposite events - that the corresponding arrows will miss:

a) Consider the event: - only one shooter hits the target. This event consists of two incompatible outcomes:

1st shooter will hit and 2nd misses
or
1st will miss and 2nd will hit.

On the tongue event algebras this fact can be written as:

First, we use the theorem of addition of probabilities of incompatible events, then - the theorem of multiplication of probabilities of independent events:

is the probability that there will be only one hit.

b) Consider the event: - at least one of the shooters will hit the target.

First of all, LET'S THINK - what does the condition "AT LEAST ONE" mean? In this case, this means that either the 1st shooter will hit (the 2nd will miss) or 2nd (1st misses) or both arrows at once - a total of 3 incompatible outcomes.

Method one: given the prepared probability of the previous item, it is convenient to represent the event as the sum of the following disjoint events:

one will get (an event consisting in turn of 2 incompatible outcomes) or
If both arrows hit, we denote this event by the letter .

In this way:

According to the theorem of multiplication of probabilities of independent events:
is the probability that the 1st shooter will hit and 2nd shooter will hit.

According to the theorem of addition of probabilities of incompatible events:
is the probability of at least one hit on the target.

Method two: consider the opposite event: – both shooters will miss.

According to the theorem of multiplication of probabilities of independent events:

As a result:

Special attention pay attention to the second method - in the general case it is more rational.

In addition, there is an alternative, third way of solving, based on the theorem of summing joint events, which was silent above.

! If you are reading the material for the first time, then in order to avoid confusion, it is better to skip the next paragraph.

Method three : the events are joint, which means that their sum expresses the event “at least one shooter hits the target” (see Fig. event algebra). By theorem of addition of probabilities of joint events and the theorem of multiplication of probabilities of independent events:

Let's check: events and (0, 1 and 2 hits respectively) form a complete group, so the sum of their probabilities must be equal to one:
, which was to be verified.

Answer:

With a thorough study of the theory of probability, you will come across dozens of tasks of a militaristic content, and, which is typical, after that you will not want to shoot anyone - the tasks are almost gift. Why not make the template even simpler? Let's shorten the entry:

Solution: according to the condition: , is the probability of hitting the corresponding shooters. Then their miss probabilities are:

a) According to the theorems of addition of probabilities of incompatible and multiplication of probabilities of independent events:
is the probability that only one shooter will hit the target.

b) According to the theorem of multiplication of probabilities of independent events:
is the probability that both shooters will miss.

Then: is the probability that at least one of the shooters will hit the target.

Answer:

In practice, you can use any design option. Of course, much more often they go the short way, but one should not forget the 1st method - although it is longer, it is more meaningful - it is clearer in it, what, why and why adds up and multiplies. In some cases, a hybrid style is appropriate when capital letters It is convenient to indicate only some events.

Similar tasks for independent solution:

Task 6

Two independently operating sensors are installed for fire alarm. The probabilities that the sensor will operate during a fire are 0.5 and 0.7 for the first and second sensors, respectively. Find the probability that in a fire:

a) both sensors will fail;
b) both sensors will work.
c) Using addition theorem for the probabilities of events forming a complete group, find the probability that only one sensor will operate during a fire. Check the result by direct calculation of this probability (using addition and multiplication theorems).

Here, the independence of the operation of devices is directly spelled out in the condition, which, by the way, is an important clarification. The sample solution is designed in an academic style.

What if, in a similar problem, the same probabilities are given, for example, 0.9 and 0.9? You need to decide exactly the same! (which, in fact, has already been demonstrated in the example with two coins)

Task 7

The probability of hitting the target by the first shooter with one shot is 0.8. The probability that the target is not hit after the first and second shooters shoot one shot is 0.08. What is the probability of hitting the target by the second shooter with one shot?

And this is a small puzzle, which is framed in a short way. The condition can be reformulated more concisely, but I will not remake the original - in practice, I have to delve into more ornate fabrications.

Meet him - he is the one who cut an unmeasured amount of details for you =):

Task 8

A worker operates three machines. The probability that during the shift the first machine will require adjustment is 0.3, the second - 0.75, the third - 0.4. Find the probability that during the shift:

a) all machines will require adjustment;
b) only one machine will require adjustment;
c) at least one machine will require adjustment.

Solution: since the condition does not say anything about a single technological process, then the operation of each machine should be considered independent of the operation of other machines.

By analogy with Task No. 5, here you can enter into consideration events consisting in the fact that the corresponding machines will require adjustment during the shift, write down the probabilities , find the probabilities of opposite events, etc. But with three objects, I don’t really want to draw up the task like that - it will turn out long and tedious. Therefore, it is noticeably more profitable to use the “quick” style here:

By condition: - the probability that during the shift the corresponding machines will require tuning. Then the probabilities that they will not require attention are:

One of the readers found a cool typo here, I won’t even correct it =)

a) According to the theorem of multiplication of probabilities of independent events:
is the probability that during the shift all three machines will require adjustment.

b) The event "During the shift, only one machine will require adjustment" consists of three incompatible outcomes:

1) 1st machine will require attention and 2nd machine will not require and 3rd machine will not require
or:
2) 1st machine will not require attention and 2nd machine will require and 3rd machine will not require
or:
3) 1st machine will not require attention and 2nd machine will not require and 3rd machine will require.

According to the theorems of addition of probabilities of incompatible and multiplication of probabilities of independent events:

- the probability that during the shift only one machine will require adjustment.

I think by now it should be clear to you where the expression came from

c) Calculate the probability that the machines will not require adjustment, and then the probability of the opposite event:
– the fact that at least one machine will require adjustment.

Answer:

Item "ve" can also be solved through the sum , where is the probability that during the shift only two machines will require adjustment. This event, in turn, includes 3 incompatible outcomes, which are signed by analogy with the “be” item. Try to find the probability yourself to check the whole problem with the help of equality.

Task 9

Three guns fired a volley at the target. The probability of hitting with one shot only from the first gun is 0.7, from the second - 0.6, from the third - 0.8. Find the probability that: 1) at least one projectile hits the target; 2) only two projectiles will hit the target; 3) the target will be hit at least twice.

Solution and answer at the end of the lesson.

And again about coincidences: in the event that, by condition, two or even all values ​​of the initial probabilities coincide (for example, 0.7; 0.7 and 0.7), then exactly the same solution algorithm should be followed.

In conclusion of the article, we will analyze another common puzzle:

Task 10

The shooter hits the target with the same probability with each shot. What is this probability if the probability of at least one hit in three shots is 0.973.

Solution: denote by - the probability of hitting the target with each shot.
and through - the probability of a miss with each shot.

Let's write down the events:
- with 3 shots, the shooter will hit the target at least once;
- the shooter will miss 3 times.

According to the condition, then the probability of the opposite event:

On the other hand, according to the theorem of multiplication of probabilities of independent events:

In this way:

- the probability of a miss with each shot.

As a result:
is the probability of hitting each shot.

Answer: 0,7

Simple and elegant.

In the considered problem, additional questions can be raised about the probability of only one hit, only two hits, and the probability of three hits on the target. The solution scheme will be exactly the same as in the two previous examples:

However, the fundamental substantive difference is that there are repeated independent tests, which are performed sequentially, independently of each other and with the same probability of outcomes.