Recall the necessary information about complex numbers.

Complex number is an expression of the form a + bi, where a, b are real numbers, and i- so-called imaginary unit, the symbol whose square is -1, i.e. i 2 = -1. Number a called real part, and the number b - imaginary part complex number z = a + bi. If b= 0, then instead of a + 0i write simply a. It can be seen that the real numbers are special case complex numbers.

Arithmetic operations on complex numbers are the same as on real ones: they can be added, subtracted, multiplied and divided by each other. Addition and subtraction proceed according to the rule ( a + bi) ± ( c + di) = (a ± c) + (b ± d)i, and multiplication - according to the rule ( a + bi) · ( c + di) = (ac – bd) + (ad + bc)i(here it is just used that i 2 = -1). Number = a – bi called complex conjugate To z = a + bi. Equality z · = a 2 + b 2 allows you to understand how to divide one complex number by another (non-zero) complex number:

(For instance, .)

Complex numbers have a convenient and visual geometric representation: the number z = a + bi can be represented as a vector with coordinates ( a; b) on the Cartesian plane (or, which is almost the same, a point - the end of the vector with these coordinates). In this case, the sum of two complex numbers is depicted as the sum of the corresponding vectors (which can be found by the parallelogram rule). By the Pythagorean theorem, the length of the vector with coordinates ( a; b) is equal to . This value is called module complex number z = a + bi and is denoted by | z|. The angle that this vector makes with the positive direction of the x-axis (counted counterclockwise) is called argument complex number z and denoted by Arg z. The argument is not uniquely defined, but only up to the addition of a multiple of 2 π radians (or 360°, if you count in degrees) - after all, it is clear that turning through such an angle around the origin will not change the vector. But if the vector of length r forms an angle φ with the positive direction of the x-axis, then its coordinates are equal to ( r cos φ ; r sin φ ). Hence it turns out trigonometric notation complex number: z = |z| (cos(Arg z) + i sin(Arg z)). It is often convenient to write complex numbers in this form, because it greatly simplifies calculations. Multiplication of complex numbers in trigonometric form looks very simple: z one · z 2 = |z 1 | · | z 2 | (cos(Arg z 1+arg z 2) + i sin(Arg z 1+arg z 2)) (when multiplying two complex numbers, their moduli are multiplied and the arguments are added). From here follow De Moivre formulas: z n = |z|n(cos( n(Arg z)) + i sin( n(Arg z))). With the help of these formulas, it is easy to learn how to extract roots of any degree from complex numbers. Root nth degrees from number z is such a complex number w, what w n = z. It's clear that , And where k can take any value from the set (0, 1, ..., n- one). This means that there is always exactly n roots n th degree from a complex number (on the plane they are located at the vertices of a regular n-gon).

FEDERAL AGENCY FOR EDUCATION

STATE EDUCATIONAL INSTITUTION

HIGHER PROFESSIONAL EDUCATION

"VORONEZH STATE PEDAGOGICAL UNIVERSITY"

CHAIR OF AGLEBRA AND GEOMETRY

Complex numbers

(favorite tasks)

FINAL QUALIFICATION WORK

specialty 050201.65 mathematics

(with additional specialty 050202.65 informatics)

Completed by: 5th year student

physical and mathematical

faculty

Scientific adviser:

VORONEZH - 2008

1. Introduction……………………………………………………...…………..…

2. Complex numbers (selected problems)

2.1. Complex numbers in algebraic form….……...……….….

2.2. Geometric interpretation of complex numbers…………..…

2.3. Trigonometric form of complex numbers

2.4. Application of the theory of complex numbers to the solution of equations of the 3rd and 4th degree……………..…………………………………………………………

2.5. Complex numbers and parameters………...……………………...….

3. Conclusion…………………………………………………….................

4. List of references………………………….………………….............

1. Introduction

In the math program school course number theory is introduced on examples of sets of natural numbers, integers, rational, irrational, i.e. on the set of real numbers whose images fill the entire number line. But already in the 8th grade there is not enough stock of real numbers, solving quadratic equations with a negative discriminant. Therefore, it was necessary to replenish the stock of real numbers with complex numbers for which the square root of negative number has the meaning.

The choice of the topic "Complex Numbers", as the topic of my final qualification work, is that the concept of a complex number expands students' knowledge about number systems, about solving a wide class of problems of both algebraic and geometric content, about solving algebraic equations of any degree and about solving problems with parameters.

In this thesis work, the solution of 82 problems is considered.

The first part of the main section "Complex Numbers" provides solutions to problems with complex numbers in algebraic form, defines the operations of addition, subtraction, multiplication, division, conjugation for complex numbers in algebraic form, the degree of an imaginary unit, the modulus of a complex number, and also sets out the rule extraction square root from a complex number.

In the second part, problems are solved for the geometric interpretation of complex numbers in the form of points or vectors of the complex plane.

The third part deals with operations on complex numbers in trigonometric form. Formulas are used: De Moivre and extraction of a root from a complex number.

The fourth part is devoted to solving equations of the 3rd and 4th degrees.

When solving problems of the last part "Complex Numbers and Parameters", the information given in the previous parts is used and consolidated. A series of problems of the chapter is devoted to the definition of families of lines in the complex plane, given by the equations(inequalities) with a parameter. In part of the exercises, you need to solve equations with a parameter (over the field C). There are tasks where a complex variable simultaneously satisfies a number of conditions. A feature of solving the problems of this section is the reduction of many of them to the solution of equations (inequalities, systems) of the second degree, irrational, trigonometric with a parameter.

A feature of the presentation of the material of each part is the initial introduction of the theoretical foundations, and subsequently their practical application in solving problems.

In the end thesis a list of used literature is presented. In most of them, the theoretical material is presented in sufficient detail and in an accessible way, solutions of some problems are considered, and practical tasks for independent solution. Special attention I would like to refer to sources such as:

1. Gordienko N.A., Belyaeva E.S., Firstov V.E., Serebryakova I.V. Complex numbers and their applications: Textbook. . Material study guide presented in the form of lectures and practical exercises.

2. Shklyarsky D.O., Chentsov N.N., Yaglom I.M. Selected problems and theorems of elementary mathematics. Arithmetic and Algebra. The book contains 320 problems related to algebra, arithmetic and number theory. By their nature, these tasks differ significantly from standard school tasks.

2. Complex numbers (selected problems)

2.1. Complex numbers in algebraic form

The solution of many problems in mathematics and physics is reduced to solving algebraic equations, i.e. equations of the form

,

where a0 , a1 , …, an are real numbers. Therefore, the study of algebraic equations is one of the most important questions in mathematics. For example, a quadratic equation with a negative discriminant has no real roots. The simplest such equation is the equation

.

In order for this equation to have a solution, it is necessary to expand the set of real numbers by adding to it the root of the equation

.

Let's denote this root as

. Thus, by definition, , or ,

hence,

. is called the imaginary unit. With its help and with the help of a pair of real numbers, an expression of the form is formed.

The resulting expression was called complex numbers because they contained both real and imaginary parts.

So, complex numbers are called expressions of the form

, and are real numbers, and is some symbol that satisfies the condition . The number is called the real part of the complex number, and the number is called its imaginary part. The symbols , are used to designate them.

Complex numbers of the form

are real numbers and, therefore, the set of complex numbers contains the set of real numbers.

Complex numbers of the form

are called purely imaginary. Two complex numbers of the form and are called equal if their real and imaginary parts are equal, i.e. if the equalities , .

The algebraic notation of complex numbers makes it possible to perform operations on them according to the usual rules of algebra.

The sum of two complex numbers

and is called a complex number of the form .

The product of two complex numbers

Complex numbers

Imaginary and complex numbers. Abscissa and ordinate

complex number. Conjugate complex numbers.

Operations with complex numbers. Geometric

representation of complex numbers. complex plane.

Modulus and argument of a complex number. trigonometric

complex number form. Operations with complex

numbers in trigonometric form. Moivre formula.

Basic information about imaginary and complex numbers are given in the section "Imaginary and complex numbers". The need for these numbers of a new type appeared when solving quadratic equations for the caseD< 0 (здесь Dis the discriminant of the quadratic equation). For a long time, these numbers did not find physical use, which is why they were called "imaginary" numbers. However, now they are very widely used in various fields of physics.

and technology: electrical engineering, hydro- and aerodynamics, the theory of elasticity, etc.

Complex numbers are written as:a+bi. Here a and b – real numbers , a i – imaginary unit. e. i 2 = –1. Number a called abscissa, a b - ordinatecomplex numbera + b .Two complex numbersa+bi and a-bi called conjugate complex numbers.

Main agreements:

1. Real numberacan also be written in the formcomplex number:a + 0 i or a - 0 i. For example, entries 5 + 0i and 5 - 0 imean the same number 5 .

2. Complex number 0 + bicalled purely imaginary number. Recordingbimeans the same as 0 + bi.

3. Two complex numbersa+bi andc + diare considered equal ifa = c and b = d. Otherwise complex numbers are not equal.

Addition. The sum of complex numbersa+bi and c + diis called a complex number (a+c ) + (b+d ) i .In this way, when added complex numbers, their abscissas and ordinates are added separately.

This definition follows the rules for dealing with ordinary polynomials.

Subtraction. The difference between two complex numbersa+bi(reduced) and c + di(subtracted) is called a complex number (a-c ) + (b-d ) i .

In this way, when subtracting two complex numbers, their abscissas and ordinates are subtracted separately.

Multiplication. The product of complex numbersa+bi and c + di is called a complex number.

(ac-bd ) + (ad+bc ) i .This definition stems from two requirements:

1) numbers a+bi and c + dishould multiply like algebraic binomials,

2) number ihas the main property:i 2 = – 1.

EXAMPLE ( a + bi )(a-bi) = a 2 +b 2 . Hence, work

two conjugate complex numbers is equal to the real

positive number.

Division. Divide a complex numbera+bi (divisible) to anotherc + di(divider) - means to find the third numbere + fi(chat), which, when multiplied by a divisorc + di, which results in the dividenda + b .

If the divisor is not zero, division is always possible.

EXAMPLE Find (8+i ) : (2 – 3 i) .

Solution. Let's rewrite this ratio as a fraction:

Multiplying its numerator and denominator by 2 + 3i

AND after performing all the transformations, we get:

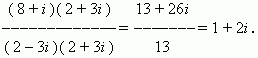
Geometric representation of complex numbers. Real numbers are represented by points on the number line:

Here is the point Ameans number -3, dotB is the number 2, and O- zero. In contrast, complex numbers are represented by dots on coordinate plane. For this, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see fig.). This coordinate system is called complex plane .

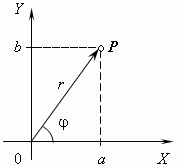
module complex number is called the length of the vectorOP, depicting a complex number on the coordinate ( comprehensive) plane. Complex number modulusa+bi denoted by | a+bi| or letter r

§ 1. Complex numbers: definitions, geometric interpretation, operations in algebraic, trigonometric and exponential forms

Definition of a complex number

Complex equalities

Geometric representation of complex numbers

Modulus and argument of a complex number

Algebraic and trigonometric forms of a complex number

The exponential form of a complex number

Euler formulas

§ 2. Entire functions (polynomials) and their basic properties. Solution of algebraic equations on the set of complex numbers

Definition of an algebraic equation of the th degree

Basic properties of polynomials

Examples of solving algebraic equations on the set of complex numbers

Questions for self-examination

Glossary

§ 1. Complex numbers: definitions, geometric interpretation, operations in algebraic, trigonometric and exponential forms

Definition of a complex number ( Formulate the definition of a complex number)

A complex number z is an expression of the following form:

Complex number in algebraic form,(1)

Where x, y Î;

- complex conjugate number z ;

- opposite number number z ;

- complex zero ;

- this is the set of complex numbers.

1)z = 1 + iÞ Re z= 1, Im z = 1, = 1 – i, = –1 – i ;

2)z = –1 + iÞ Re z= –1, Im z = , = –1 – i, = –1 –i ;

3)z = 5 + 0i= 5 Þ Re z= 5, Im z = 0, = 5 – 0i = 5, = –5 – 0i = –5

Þ if Im z= 0, then z = x- real number;

4)z = 0 + 3i = 3iÞ Re z= 0, Im z = 3, = 0 – 3i = –3i , = –0 – 3i = – 3i

Þ if Re z= 0, then z = iy - pure imaginary number.

Complex equalities (Formulate the meaning of complex equality)

1) ;

2) .

One complex equality is equivalent to a system of two real equalities. These real equalities are obtained from the complex equality by separating the real and imaginary parts.

1) ;

2) .

Geometric representation of complex numbers ( What is the geometric representation of complex numbers?)

Complex number z represented by a dot ( x , y) on the complex plane or the radius vector of this point.

Sign z in the second quadrant means that the Cartesian coordinate system will be used as the complex plane.

Modulus and argument of a complex number ( What is the modulus and argument of a complex number?)

The modulus of a complex number is a non-negative real number

.(2)

Geometrically, the modulus of a complex number is the length of the vector representing the number z, or the polar radius of a point ( x , y).

Draw the following numbers on the complex plane and write them in trigonometric form.

1)z = 1 + i Þ

,

Þ

Þ ;

,

Þ

Þ ;

,

5),

that is, for z = 0 it will be

, j indefined.

Arithmetic operations on complex numbers (Give definitions and list the main properties of arithmetic operations on complex numbers.)

Addition (subtraction) of complex numbers

z 1 ± z 2 = (x 1 + iy 1)±( x 2 + iy 2) = (x 1 ± x 2) + i (y 1 ± y 2),(5)

that is, when adding (subtracting) complex numbers, their real and imaginary parts are added (subtracted).

1)(1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i ;

2)(1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i .

Basic properties of addition

1)z 1 + z 2 = z 2 + z 1;

2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);

3)z 1 – z 2 = z 1 + (– z 2);

4)z + (–z) = 0;

Multiplication of complex numbers in algebraic form

z 1∙z 2 = (x 1 + iy 1)∙(x 2 + iy 2) = x 1x 2 + x 1iy 2 + iy 1x 2 + i 2y 1y 2 = (6)

= (x 1x 2 – y 1y 2) + i (x 1y 2 + y 1x 2),

that is, the multiplication of complex numbers in algebraic form is carried out according to the rule of algebraic multiplication of a binomial by a binomial, followed by replacement and reduction of similar ones in real and imaginary terms.

1)(1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i 2 = 2 – 3i + 2i + 3 = 5 – i ;

2)(1 + 4i)∙(1 – 4i) = 1 – 42 i 2 = 1 + 16 = 17;

3)(2 + i)2 = 22 + 4i + i 2 = 3 + 4i .

Multiplication of complex numbers trigonometric form

z 1∙z 2 = r 1(cos j 1 + i sin j 1)× r 2(cos j 2 + i sin j 2) =

= r 1r 2(cos j 1cos j 2 + i cos j 1sin j 2 + i sin j 1cos j 2 + i 2 sin j 1sin j 2) =

= r 1r 2((cos j 1cos j 2-sin j 1sin j 2) + i(cos j 1sin j 2+ sin j 1cos j 2))

The product of complex numbers in trigonometric form, that is, when complex numbers are multiplied in trigonometric form, their moduli are multiplied and the arguments are added.

Basic properties of multiplication

1)z 1× z 2 = z 2× z 1 - commutativity;

2)z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×( z 2× z 3) - associativity;

3)z 1×( z 2 + z 3) = z 1× z 2 + z 1× z 3 - distributivity with respect to addition;

4)z×0 = 0; z×1 = z ;

Division of complex numbers

Division is the inverse of multiplication, so

if z × z 2 = z 1 and z 2 ¹ 0, then .

When performing division in algebraic form, the numerator and denominator of the fraction are multiplied by the complex conjugate of the denominator:

Division of complex numbers in algebraic form.(7)

When performing division in trigonometric form, modules are divided and arguments are subtracted:

Division of complex numbers in trigonometric form.(8)

2)
.

Raising a complex number to a natural power

Raising to a natural power is more convenient to perform in trigonometric form:

Moivre formula,(9)

that is, when a complex number is raised to a natural power, its modulus is raised to that power, and the argument is multiplied by the exponent.

Calculate (1 + i)10.

Remarks

1. When performing operations of multiplication and raising to a natural power in trigonometric form, angle values ​​\u200b\u200bcan be obtained outside of one full turn. But they can always be reduced to angles or by dropping an integer number of complete revolutions according to the periodicity properties of the functions and .

2. Meaning is called the principal value of the argument of a complex number;

in this case, the values ​​of all possible angles denote ;

it's obvious that , .

root extraction natural degree from a complex number

Euler formulas(16)

for which trigonometric functions and a real variable are expressed in terms of exponential function(exponent) with a purely imaginary exponent.

§ 2. Entire functions (polynomials) and their basic properties. Solution of algebraic equations on the set of complex numbers

Two polynomials of the same degree n are identically equal to each other if and only if their coefficients coincide at the same powers of the variable x, that is

Proof

w Identity (3) holds for "xн (or "xн)

Þ it is valid for ; substituting , we get an = bn .

Let us mutually annihilate the terms in (3) an and bn and divide both parts by x :

This identity is also true for " x, including when x = 0

Þ assuming x= 0, we get an – 1 = bn – 1.

Mutually annihilate in (3") terms an– 1 and a n– 1 and divide both parts by x, as a result we get

Continuing the argument similarly, we get that an – 2 = bn –2, …, a 0 = b 0.

Thus, it is proved that from the identical equality of 2-x polynomials follows the coincidence of their coefficients at the same degrees x .

The converse statement is rightly obvious, i.e. if two polynomials have the same all coefficients, then they are the same functions, therefore, their values ​​are the same for all values ​​of the argument, which means their identical equality. Property 1 is proved completely. v

When dividing a polynomial PN (x) to the difference ( x – X 0) the remainder is equal to PN (x 0), that is

Bezout's theorem,(4)

where Qn – 1(x) - the integer part of division, is a polynomial of degree ( n – 1).

Proof

w Let's write the division formula with a remainder:

PN (x) = (x – X 0)∙Qn – 1(x) + A ,

where Qn – 1(x) - degree polynomial ( n – 1),

A- the remainder, which is a number due to the well-known algorithm for dividing a polynomial into a binomial "in a column".

This equality is true for " x, including when x = X 0 Þ

PN (x 0) = (x 0 – x 0)× Qn – 1(x 0) + A Þ

A = PN (X 0), h.t.d. v

Corollary from Bezout's theorem. On the division of a polynomial by a binomial without a remainder

If number X 0 is the zero of the polynomial, then this polynomial is divisible by the difference ( x – X 0) without a remainder, that is

Þ .(5)

1) , because P 3(1) º 0

2) , because P 4(–2) º 0

3) because P 2(–1/2) º 0

Division of polynomials into binomials "in a column":

_

_

_

_

_

Every polynomial of degree n ³ 1 has at least one zero, real or complex

The proof of this theorem is beyond the scope of our course. Therefore, we accept the theorem without proof.

Let's work on this theorem and on Bezout's theorem with a polynomial PN (x).

After n-fold application of these theorems, we obtain that

where a 0 is the coefficient at x n v PN (x).

Corollary from the fundamental theorem of algebra. On the decomposition of a polynomial into linear factors

Any polynomial of degree on the set of complex numbers decomposes into n linear factors, that is

Decomposition of a polynomial into linear factors, (6)

where x1, x2, ... xn are the zeros of the polynomial.

At the same time, if k numbers from the set X 1, X 2, … xn coincide with each other and with the number a, then in the product (6) the factor ( x– a) k. Then the number x= a is called k-fold zero polynomial PN ( x) . If k= 1, then zero is called simple zero polynomial PN ( x) .

1)P 4(x) = (x – 2)(x– 4)3 Þ x 1 = 2 - simple zero, x 2 = 4 - triple zero;

2)P 4(x) = (x – i)4 x = i- zero multiplicity 4.

Property 4 (on the number of roots of an algebraic equation)

Any algebraic equation Pn(x) = 0 of degree n has exactly n roots on the set of complex numbers, if each root is counted as many times as its multiplicity.

1)x 2 – 4x+ 5 = 0 - algebraic equation of the second degree

Þ x 1.2 = 2 ± = 2 ± i- two roots;

2)x 3 + 1 = 0 - algebraic equation of the third degree

Þ x 1,2,3 = - three roots;

3)P 3(x) = x 3 + x 2 – x– 1 = 0 x 1 = 1, because P 3(1) = 0.

Divide the polynomial P 3(x) on the ( x – 1):

x 3	+	x 2	–	x	–	1	x – 1
x 3	–	x 2	x 2 + 2x +1
2x 2	–	x
2x 2	–	2x
x	–	1
x	–	1
0

Initial Equation

P 3(x) = x 3 + x 2 – x– 1 = 0 Û( x – 1)(x 2 + 2x+ 1) = 0 w( x – 1)(x + 1)2 = 0

Þ x 1 = 1 - simple root, x 2 \u003d -1 - double root.

1) are paired complex conjugate roots;

Any polynomial with real coefficients decomposes into a product of linear and quadratic functions with real coefficients.

Proof

w Let x 0 = a + bi- polynomial zero PN (x). If all the coefficients of this polynomial are real numbers, then is also its zero (by property 5).

We calculate the product of binomials :

complex number polynomial equation

Received ( x – a)2 + b 2 - square trinomial with real coefficients.

Thus, any pair of binomials with complex conjugate roots in formula (6) leads to a square trinomial with real coefficients. v

1)P 3(x) = x 3 + 1 = (x + 1)(x 2 – x + 1);

2)P 4(x) = x 4 – x 3 + 4x 2 – 4x = x (x –1)(x 2 + 4).

Examples of solving algebraic equations on the set of complex numbers ( Give examples of solving algebraic equations on the set of complex numbers)

1. Algebraic equations of the first degree:

, is the only simple root.

2. Quadratic equations:

, - always has two roots (different or equal).

1) .

3. Two-term degree equations:

, - always has different roots.

,

Answer: , .

4. Solve the cubic equation.

An equation of the third degree has three roots (real or complex), and each root must be counted as many times as its multiplicity. Since all the coefficients of this equation are real numbers, the complex roots of the equation, if any, will be paired complex conjugate.

By selection we find the first root of the equation , since .

By a corollary of Bezout's theorem. We calculate this division "in a column":

_
_
_

Representing the polynomial as a product of a linear and square factor, we get:

.

We find other roots as the roots of the quadratic equation:

Answer: , .

5. Compose an algebraic equation of the least degree with real coefficients, if it is known that the numbers x 1 = 3 and x 2 = 1 + i are its roots, and x 1 is a double root, and x 2 - simple.

The number is also the root of the equation, because the coefficients of the equation must be real.

In total, the desired equation has 4 roots: x 1, x 1,x 2, . Therefore, its degree is 4. We compose a polynomial of the 4th degree with zeros x

11. What is complex zero?

13. Formulate the meaning of complex equality.

15. What is the modulus and argument of a complex number?

17. What is the argument of a complex number?

18. What is the name or meaning of the formula?

19. Explain the meaning of the notation in this formula:

27. Give definitions and list the main properties of arithmetic operations on complex numbers.

28. What is the name or meaning of the formula?

29. Explain the meaning of the notation in this formula:

31. What is the name or meaning of the formula?

32. Explain the meaning of the notation in this formula:

34. What is the name or meaning of the formula?

35. Explain the meaning of the notation in this formula:

61. List the main properties of polynomials.

63. Formulate a property about dividing a polynomial by a difference (x - x0).

65. What is the name or meaning of the formula?

66. Explain the meaning of the notation in this formula:

67. ⌂ .

69. Formulate the theorem the theorem of algebra is basic.

70. What is the name or meaning of the formula?

71. Explain the meaning of the notation in this formula:

75. Formulate a property about the number of roots of an algebraic equation.

78. Formulate a property about the decomposition of a polynomial with real coefficients into linear and quadratic factors.

Glossary

The k-fold zero of a polynomial is called... (p. 18)

an algebraic polynomial is called... (p. 14)

algebraic equation n degree is called... (p. 14)

the algebraic form of a complex number is called... (p. 5)

the argument of a complex number is... (p. 4)

the real part of the complex number z is... (page 2)

the complex conjugate is... (page 2)

complex zero is... (page 2)

a complex number is called... (p. 2)

the nth root of a complex number is called... (p. 10)

the root of the equation is called ... (p. 14)

polynomial coefficients are... (p. 14)

the imaginary unit is... (page 2)

the imaginary part of a complex number z is... (page 2)

the modulus of a complex number is called... (p. 4)

the zero of a function is called... (p. 14)

the exponential form of a complex number is called... (p. 11)

a polynomial is called... (p. 14)

simple zero polynomial is called... (p. 18)

the opposite number is... (page 2)

the degree of a polynomial is... (p. 14)

the trigonometric form of a complex number is called... (p. 5)

De Moivre's formula is... (p. 9)

Euler's formulas are... (p. 13)

an entire function is called... (p. 14)

a purely imaginary number is... (p. 2)

To solve problems with complex numbers, you need to understand the basic definitions. The main objective of this review article is to explain what complex numbers are and present methods for solving basic problems with complex numbers. Thus, a complex number is a number of the form z = a + bi, where a, b- real numbers, which are called the real and imaginary parts of a complex number, respectively, and denote a = Re(z), b=Im(z).
i is called the imaginary unit. i 2 \u003d -1. In particular, any real number can be considered complex: a = a + 0i, where a is real. If a = 0 and b ≠ 0, then the number is called purely imaginary.

We now introduce operations on complex numbers.
Consider two complex numbers z 1 = a 1 + b 1 i and z 2 = a 2 + b 2 i.

Consider z = a + bi.

The set of complex numbers extends the set of real numbers, which in turn extends the set rational numbers etc. This chain of investments can be seen in the figure: N - integers, Z are integers, Q are rational, R are real, C are complex.

Representation of complex numbers

Algebraic notation.

Consider a complex number z = a + bi, this form of writing a complex number is called algebraic. We have already discussed this form of writing in detail in the previous section. Quite often use the following illustrative drawing

trigonometric form.

It can be seen from the figure that the number z = a + bi can be written differently. It's obvious that a = rcos(φ), b = rsin(φ), r=|z|, hence z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π) is called the argument of a complex number. This representation of a complex number is called trigonometric form. The trigonometric form of notation is sometimes very convenient. For example, it is convenient to use it for raising a complex number to an integer power, namely, if z = rcos(φ) + rsin(φ)i, then z n = r n cos(nφ) + r n sin(nφ)i, this formula is called De Moivre's formula.

Demonstrative form.

Consider z = rcos(φ) + rsin(φ)i is a complex number in trigonometric form, we write it in a different form z = r(cos(φ) + sin(φ)i) = re iφ, the last equality follows from the Euler formula, so we get new form complex number entries: z = re iφ, which is called demonstrative. This form of notation is also very convenient for raising a complex number to a power: z n = r n e inφ, here n not necessarily an integer, but can be an arbitrary real number. This form of writing is quite often used to solve problems.

Fundamental theorem of higher algebra

Imagine that we have a quadratic equation x 2 + x + 1 = 0 . It is obvious that the discriminant of this equation is negative and it has no real roots, but it turns out that this equation has two different complex roots. So, the main theorem of higher algebra states that any polynomial of degree n has at least one complex root. It follows from this that any polynomial of degree n has exactly n complex roots, taking into account their multiplicity. This theorem is a very important result in mathematics and is widely applied. A simple consequence of this theorem is the following result: there are exactly n distinct n-degree roots of unity.

Main types of tasks

This section will cover the main types simple tasks to complex numbers. Conventionally, problems on complex numbers can be divided into the following categories.

• Performing simple arithmetic operations on complex numbers.
• Finding the roots of polynomials in complex numbers.
• Raising complex numbers to a power.
• Extraction of roots from complex numbers.
• Application of complex numbers to solve other problems.

Now consider the general methods for solving these problems.

The simplest arithmetic operations with complex numbers are performed according to the rules described in the first section, but if complex numbers are presented in trigonometric or exponential forms, then in this case they can be converted into algebraic form and perform operations according to known rules.

Finding the roots of polynomials usually comes down to finding the roots of a quadratic equation. Suppose we have a quadratic equation, if its discriminant is non-negative, then its roots will be real and are found according to a well-known formula. If the discriminant is negative, then D = -1∙a 2, where a is a certain number, then we can represent the discriminant in the form D = (ia) 2, hence √D = i|a|, and then you can use the already known formula for the roots of the quadratic equation.

Example. Let's return to the quadratic equation mentioned above x 2 + x + 1 = 0.
Discriminant - D \u003d 1 - 4 ∙ 1 \u003d -3 \u003d -1 (√3) 2 \u003d (i√3) 2.
Now we can easily find the roots:

Raising complex numbers to a power can be done in several ways. If you want to raise a complex number in algebraic form in small degree(2 or 3), then you can do this by direct multiplication, but if the degree is larger (in problems it is often much larger), then you need to write this number in trigonometric or exponential forms and use already known methods.

Example. Consider z = 1 + i and raise to the tenth power.
We write z in exponential form: z = √2 e iπ/4 .
Then z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
Let's return to the algebraic form: z 10 = -32i.

Extracting roots from complex numbers is the inverse operation with respect to exponentiation, so it is done in a similar way. To extract the roots, the exponential form of writing a number is often used.

Example. Find all roots of degree 3 of unity. To do this, we find all the roots of the equation z 3 = 1, we will look for the roots in exponential form.
Substitute in the equation: r 3 e 3iφ = 1 or r 3 e 3iφ = e 0 .
Hence: r = 1, 3φ = 0 + 2πk, hence φ = 2πk/3.
Various roots are obtained at φ = 0, 2π/3, 4π/3.
Hence 1 , e i2π/3 , e i4π/3 are roots.
Or in algebraic form: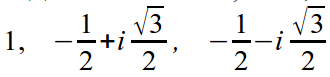

The last type of problems includes a huge variety of problems and there are no general methods for solving them. Here is a simple example of such a task:

Find the amount sin(x) + sin(2x) + sin(2x) + … + sin(nx).

Although the formulation of this problem does not in question about complex numbers, but with their help it can be easily solved. To solve it, the following representations are used:


If we now substitute this representation into the sum, then the problem is reduced to the summation of the usual geometric progression.

Conclusion

Complex numbers are widely used in mathematics, this review article discussed the basic operations on complex numbers, described several types of standard problems and briefly described general methods for solving them, for a more detailed study of the possibilities of complex numbers, it is recommended to use specialized literature.

Literature