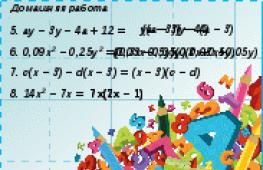Many people think that exponential inequalities It's something so complex and incomprehensible. And that learning to solve them is almost a great art, which only the Chosen are able to comprehend...

Complete nonsense! Exponential inequalities are easy. And they are always easy to solve. Well, almost always. :)

Today we will analyze this topic far and wide. This lesson will be very useful for those who are just starting to understand this section of school mathematics. Let's start with simple tasks and move on to more complex issues. There will be no tinny today, but what you will read now will be enough to solve most of the inequalities on all sorts of control and independent work. And on this your exam too.

As always, let's start with a definition. An exponential inequality is any inequality that contains an exponential function. In other words, it can always be reduced to an inequality of the form

\[((a)^(x)) \gt b\]

Where the role of $b$ can be an ordinary number, or maybe something tougher. Examples? Yes please:

\[\begin(align) & ((2)^(x)) \gt 4;\quad ((2)^(x-1))\le \frac(1)(\sqrt(2));\ quad ((2)^(((x)^(2))-7x+14)) \lt 16; \\ & ((0,1)^(1-x)) \lt 0.01;\quad ((2)^(\frac(x)(2))) \lt ((4)^(\frac (4)(x))). \\\end(align)\]

I think the meaning is clear: there is an exponential function $((a)^(x))$, it is compared with something, and then asked to find $x$. In especially clinical cases, instead of the variable $x$, they can put some function $f\left(x \right)$ and thereby complicate the inequality a little. :)

Of course, in some cases, the inequality may look more severe. For example:

\[((9)^(x))+8 \gt ((3)^(x+2))\]

Or even this:

In general, the complexity of such inequalities can be very different, but in the end they still come down to a simple construction $((a)^(x)) \gt b$. And we will somehow deal with such a design (in especially clinical cases, when nothing comes to mind, logarithms will help us). Therefore, now we will learn how to solve such simple constructions.

Solution of the simplest exponential inequalities

Let's look at something very simple. For example, here it is:

\[((2)^(x)) \gt 4\]

Obviously, the number on the right can be rewritten as a power of two: $4=((2)^(2))$. Thus, the original inequality is rewritten in a very convenient form:

\[((2)^(x)) \gt ((2)^(2))\]

And now the hands are itching to "cross out" the deuces, standing in the bases of the degrees, in order to get the answer $x \gt 2$. But before we cross out anything, let's remember the powers of two:

\[((2)^(1))=2;\quad ((2)^(2))=4;\quad ((2)^(3))=8;\quad ((2)^( 4))=16;...\]

As you can see, the larger the number in the exponent, the larger the output number. "Thanks, Cap!" one of the students will exclaim. Does it happen differently? Unfortunately, it happens. For instance:

\[((\left(\frac(1)(2) \right))^(1))=\frac(1)(2);\quad ((\left(\frac(1)(2) \ right))^(2))=\frac(1)(4);\quad ((\left(\frac(1)(2) \right))^(3))=\frac(1)(8 );...\]

Here, too, everything is logical: the greater the degree, the more times the number 0.5 is multiplied by itself (that is, it is divided in half). Thus, the resulting sequence of numbers decreases, and the difference between the first and second sequences is only in the base:

• If the base of degree $a \gt 1$, then as the exponent $n$ grows, the number $((a)^(n))$ will also grow;
• Conversely, if $0 \lt a \lt 1$, then as the exponent $n$ grows, the number $((a)^(n))$ will decrease.

Summing up these facts, we get the most important statement, on which the entire solution of exponential inequalities is based:

If $a \gt 1$, then the inequality $((a)^(x)) \gt ((a)^(n))$ is equivalent to the inequality $x \gt n$. If $0 \lt a \lt 1$, then the inequality $((a)^(x)) \gt ((a)^(n))$ is equivalent to the inequality $x \lt n$.

In other words, if the base is greater than one, you can simply remove it - the inequality sign will not change. And if the base is less than one, then it can also be removed, but the sign of inequality will also have to be changed.

Note that we have not considered the $a=1$ and $a\le 0$ options. Because in these cases there is uncertainty. Suppose how to solve an inequality of the form $((1)^(x)) \gt 3$? A one to any power will again give a one - we will never get a three or more. Those. there are no solutions.

With negative bases, it's even more interesting. Consider, for example, the following inequality:

\[((\left(-2 \right))^(x)) \gt 4\]

At first glance, everything is simple:

Right? But no! It is enough to substitute a couple of even and a couple of odd numbers instead of $x$ to make sure that the solution is wrong. Take a look:

\[\begin(align) & x=4\Rightarrow ((\left(-2 \right))^(4))=16 \gt 4; \\ & x=5\Rightarrow ((\left(-2 \right))^(5))=-32 \lt 4; \\ & x=6\Rightarrow ((\left(-2 \right))^(6))=64 \gt 4; \\ & x=7\Rightarrow ((\left(-2 \right))^(7))=-128 \lt 4. \\\end(align)\]

As you can see, the signs alternate. But there are still fractional degrees and other tin. How, for example, would you order to count $((\left(-2 \right))^(\sqrt(7)))$ (minus two raised to the root of seven)? No way!

Therefore, for definiteness, we assume that in all exponential inequalities (and equations, by the way, too) $1\ne a \gt 0$. And then everything is solved very simply:

\[((a)^(x)) \gt ((a)^(n))\Rightarrow \left[ \begin(align) & x \gt n\quad \left(a \gt 1 \right), \\ & x \lt n\quad \left(0 \lt a \lt 1 \right). \\\end(align) \right.\]

In general, once again remember the main rule: if the base in the exponential equation is greater than one, you can simply remove it; and if the base is less than one, it can also be removed, but this will change the inequality sign.

Solution examples

So, consider a few simple exponential inequalities:

\[\begin(align) & ((2)^(x-1))\le \frac(1)(\sqrt(2)); \\ & ((0,1)^(1-x)) \lt 0.01; \\ & ((2)^(((x)^(2))-7x+14)) \lt 16; \\ & ((0,2)^(1+((x)^(2))))\ge \frac(1)(25). \\\end(align)\]

The primary task is the same in all cases: to reduce the inequalities to the simplest form $((a)^(x)) \gt ((a)^(n))$. This is what we will now do with each inequality, and at the same time we will repeat the properties of powers and the exponential function. So let's go!

\[((2)^(x-1))\le \frac(1)(\sqrt(2))\]

What can be done here? Well, on the left we already have a demonstrative expression - nothing needs to be changed. But on the right there is some kind of crap: a fraction, and even a root in the denominator!

However, remember the rules for working with fractions and powers:

\[\begin(align) & \frac(1)(((a)^(n)))=((a)^(-n)); \\ & \sqrt[k](a)=((a)^(\frac(1)(k))). \\\end(align)\]

What does it mean? First, we can easily get rid of the fraction by turning it into a negative exponent. And secondly, since the denominator is the root, it would be nice to turn it into a degree - this time with a fractional exponent.

Let's apply these actions sequentially to the right side of the inequality and see what happens:

\[\frac(1)(\sqrt(2))=((\left(\sqrt(2) \right))^(-1))=((\left(((2)^(\frac( 1)(3))) \right))^(-1))=((2)^(\frac(1)(3)\cdot \left(-1 \right)))=((2)^ (-\frac(1)(3)))\]

Do not forget that when raising a degree to a power, the exponents of these degrees are added. And in general, when working with exponential equations and inequalities, it is absolutely necessary to know at least the simplest rules for working with powers:

\[\begin(align) & ((a)^(x))\cdot ((a)^(y))=((a)^(x+y)); \\ & \frac(((a)^(x)))(((a)^(y)))=((a)^(x-y)); \\ & ((\left(((a)^(x)) \right))^(y))=((a)^(x\cdot y)). \\\end(align)\]

Actually, we just applied the last rule. Therefore, our original inequality will be rewritten as follows:

\[((2)^(x-1))\le \frac(1)(\sqrt(2))\Rightarrow ((2)^(x-1))\le ((2)^(-\ frac(1)(3)))\]

Now we get rid of the deuce at the base. Since 2 > 1, the inequality sign remains the same:

\[\begin(align) & x-1\le -\frac(1)(3)\Rightarrow x\le 1-\frac(1)(3)=\frac(2)(3); \\ & x\in \left(-\infty ;\frac(2)(3) \right]. \\\end(align)\]

That's the whole solution! The main difficulty is not at all in the exponential function, but in the competent transformation of the original expression: you need to carefully and as quickly as possible bring it to its simplest form.

Consider the second inequality:

\[((0,1)^(1-x)) \lt 0,01\]

Well well. Here we are waiting for decimal fractions. As I have said many times, in any expressions with powers, you should get rid of decimal fractions - often this is the only way to see a quick and easy solution. Here's what we'll get rid of:

\[\begin(align) & 0,1=\frac(1)(10);\quad 0,01=\frac(1)(100)=((\left(\frac(1)(10) \ right))^(2)); \\ & ((0,1)^(1-x)) \lt 0,01\Rightarrow ((\left(\frac(1)(10) \right))^(1-x)) \lt ( (\left(\frac(1)(10) \right))^(2)). \\\end(align)\]

Before us is again the simplest inequality, and even with the base 1/10, i.e. less than one. Well, we remove the bases, simultaneously changing the sign from "less" to "greater", and we get:

\[\begin(align) & 1-x \gt 2; \\ & -x \gt 2-1; \\ & -x \gt 1; \\& x \lt -1. \\\end(align)\]

We got the final answer: $x\in \left(-\infty ;-1 \right)$. Please note that the answer is exactly the set, and in no case is the construction of the form $x \lt -1$. Because formally such a construction is not a set at all, but an inequality with respect to the variable $x$. Yes, it's very simple, but it's not the answer!

Important note. This inequality could be solved in another way - by reducing both parts to a power with a base greater than one. Take a look:

\[\frac(1)(10)=((10)^(-1))\Rightarrow ((\left(((10)^(-1)) \right))^(1-x)) \ lt ((\left(((10)^(-1)) \right))^(2))\Rightarrow ((10)^(-1\cdot \left(1-x \right))) \lt ((10)^(-1\cdot 2))\]

After such a transformation, we again get an exponential inequality, but with a base of 10 > 1. And this means that you can simply cross out the ten - the inequality sign will not change. We get:

\[\begin(align) & -1\cdot \left(1-x \right) \lt -1\cdot 2; \\ & x-1 \lt-2; \\ & x \lt -2+1=-1; \\ & x \lt -1. \\\end(align)\]

As you can see, the answer is exactly the same. At the same time, we saved ourselves from the need to change the sign and generally remember some rules there. :)

\[((2)^(((x)^(2))-7x+14)) \lt 16\]

However, don't let that scare you. Whatever is in the indicators, the technology for solving the inequality itself remains the same. Therefore, we note first that 16 = 2 4 . Let's rewrite the original inequality taking this fact into account:

\[\begin(align) & ((2)^(((x)^(2))-7x+14)) \lt ((2)^(4)); \\ & ((x)^(2))-7x+14 \lt 4; \\ & ((x)^(2))-7x+10 \lt 0. \\\end(align)\]

Hooray! We got the usual square inequality! The sign has not changed anywhere, since the base is a deuce - a number greater than one.

Function zeros on the number line

We arrange the signs of the function $f\left(x \right)=((x)^(2))-7x+10$ - obviously, its graph will be a parabola with branches up, so there will be “pluses” on the sides. We are interested in the region where the function is less than zero, i.e. $x\in \left(2;5 \right)$ is the answer to the original problem.

Finally, consider another inequality:

\[((0,2)^(1+((x)^(2))))\ge \frac(1)(25)\]

Again we see an exponential function with a decimal fraction in the base. Let's convert this fraction to a common fraction:

\[\begin(align) & 0,2=\frac(2)(10)=\frac(1)(5)=((5)^(-1))\Rightarrow \\ & \Rightarrow ((0 ,2)^(1+((x)^(2))))=((\left(((5)^(-1)) \right))^(1+((x)^(2) )))=((5)^(-1\cdot \left(1+((x)^(2)) \right)))\end(align)\]

In this case, we took advantage of the remark made earlier - we reduced the base to the number 5\u003e 1 in order to simplify our further decision. Let's do the same with the right side:

\[\frac(1)(25)=((\left(\frac(1)(5) \right))^(2))=((\left(((5)^(-1)) \ right))^(2))=((5)^(-1\cdot 2))=((5)^(-2))\]

Let's rewrite the original inequality, taking into account both transformations:

\[((0,2)^(1+((x)^(2))))\ge \frac(1)(25)\Rightarrow ((5)^(-1\cdot \left(1+ ((x)^(2)) \right)))\ge ((5)^(-2))\]

The bases on both sides are the same and greater than one. There are no other terms on the right and left, so we just “cross out” the fives and we get a very simple expression:

\[\begin(align) & -1\cdot \left(1+((x)^(2)) \right)\ge -2; \\ & -1-((x)^(2))\ge -2; \\ & -((x)^(2))\ge -2+1; \\ & -((x)^(2))\ge -1;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))\le 1. \\\end(align)\]

This is where you have to be careful. Many students like to simply extract Square root both parts of the inequality and write something like $x\le 1\Rightarrow x\in \left(-\infty ;-1 \right]$. You should never do this, since the root of an exact square is module, and in no case the original variable:

\[\sqrt(((x)^(2)))=\left| x\right|\]

However, working with modules is not the most pleasant experience, right? So we won't work. Instead, we simply move all the terms to the left and solve the usual inequality using the interval method:

$\begin(align) & ((x)^(2))-1\le 0; \\ & \left(x-1 \right)\left(x+1 \right)\le 0 \\ & ((x)_(1))=1;\quad ((x)_(2)) =-1; \\\end(align)$

Again, we mark the obtained points on the number line and look at the signs:

Please note: dots are shaded.

Since we were solving a non-strict inequality, all points on the graph are shaded. Therefore, the answer will be: $x\in \left[ -1;1 \right]$ is not an interval, but a segment.

In general, I would like to note that there is nothing complicated in exponential inequalities. The meaning of all the transformations that we performed today boils down to a simple algorithm:

• Find the base to which we will reduce all degrees;
• Carefully perform transformations to get an inequality of the form $((a)^(x)) \gt ((a)^(n))$. Of course, instead of the variables $x$ and $n$, there can be much more complex functions, but this does not change the meaning;
• Cross out the bases of the degrees. In this case, the inequality sign may change if the base $a \lt 1$.

In fact, this is a universal algorithm for solving all such inequalities. And everything else that will be told to you on this topic is just specific tricks and tricks to simplify and speed up the transformation. Here's one of those tricks we'll talk about now. :)

rationalization method

Consider another batch of inequalities:

\[\begin(align) & ((\text( )\!\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\!\pi \!\!\text( ))^(((x)^(2))-3x+2)); \\ & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1; \\ & ((\left(\frac(1)(3) \right))^(((x)^(2))+2x)) \gt ((\left(\frac(1)(9) \right))^(16-x)); \\ & ((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt 1. \\\end(align)\]

Well, what is so special about them? They are also lightweight. Although, stop! Is pi raised to a power? What kind of nonsense?

And how to raise the number $2\sqrt(3)-3$ to a power? Or $3-2\sqrt(2)$? The compilers of the problems obviously drank too much "Hawthorn" before sitting down to work. :)

In fact, there is nothing wrong with these tasks. Let me remind you: an exponential function is an expression of the form $((a)^(x))$, where the base $a$ is any positive number, except for one. The number π is positive - we already know this. The numbers $2\sqrt(3)-3$ and $3-2\sqrt(2)$ are also positive - this is easy to see if we compare them with zero.

It turns out that all these “terrifying” inequalities are no different from the simple ones discussed above? And they do it the same way? Yes, absolutely right. However, using their example, I would like to consider one trick that saves a lot of time on independent work and exams. We will talk about the method of rationalization. So attention:

Any exponential inequality of the form $((a)^(x)) \gt ((a)^(n))$ is equivalent to the inequality $\left(xn \right)\cdot \left(a-1 \right) \gt 0 $.

That's the whole method. :) Did you think that there would be some kind of next game? Nothing like this! But this simple fact, written literally in one line, will greatly simplify our work. Take a look:

\[\begin(matrix) ((\text( )\!\!\pi\!\!\text( ))^(x+7)) \gt ((\text( )\!\!\pi\ !\!\text( ))^(((x)^(2))-3x+2)) \\ \Downarrow \\ \left(x+7-\left(((x)^(2)) -3x+2 \right) \right)\cdot \left(\text( )\!\!\pi\!\!\text( )-1 \right) \gt 0 \\\end(matrix)\]

Here are no more exponential functions! And you don't have to remember whether the sign changes or not. But there is new problem: what to do with the fucking multiplier \[\left(\text( )\!\!\pi\!\!\text( )-1 \right)\]? We don't know what the exact value of pi is. However, the captain seems to hint at the obvious:

\[\text( )\!\!\pi\!\!\text( )\approx 3,14... \gt 3\Rightarrow \text( )\!\!\pi\!\!\text( )-1 \gt 3-1=2\]

In general, the exact value of π doesn’t bother us much - it’s only important for us to understand that in any case $\text( )\!\!\pi\!\!\text( )-1 \gt 2$, t .e. is a positive constant, and we can divide both sides of the inequality by it:

\[\begin(align) & \left(x+7-\left(((x)^(2))-3x+2 \right) \right)\cdot \left(\text( )\!\! \pi\!\!\text( )-1 \right) \gt 0 \\ & x+7-\left(((x)^(2))-3x+2 \right) \gt 0; \\ & x+7-((x)^(2))+3x-2 \gt 0; \\ & -((x)^(2))+4x+5 \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))-4x-5 \lt 0; \\ & \left(x-5 \right)\left(x+1 \right) \lt 0. \\\end(align)\]

As you can see, at a certain point, we had to divide by minus one, and the inequality sign changed. At the end, I expanded the square trinomial according to the Vieta theorem - it is obvious that the roots are equal to $((x)_(1))=5$ and $((x)_(2))=-1$. Then everything is solved by the classical method of intervals:

We solve the inequality by the method of intervals

All points are punctured because the original inequality is strict. We are interested in the area with negative values, so the answer is $x\in \left(-1;5 \right)$. That's the solution. :)

Let's move on to the next task:

\[((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1\]

Everything is simple here, because there is a unit on the right. And we remember that a unit is any number raised to the power of zero. Even if this number is an irrational expression, standing at the base on the left:

\[\begin(align) & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt 1=((\left(2 \sqrt(3)-3\right))^(0)); \\ & ((\left(2\sqrt(3)-3 \right))^(((x)^(2))-2x)) \lt ((\left(2\sqrt(3)-3 \right))^(0)); \\\end(align)\]

So let's rationalize:

\[\begin(align) & \left(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-3-1 \right) \lt 0; \\ & \left(((x)^(2))-2x-0 \right)\cdot \left(2\sqrt(3)-4 \right) \lt 0; \\ & \left(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0. \\\end(align)\ ]

It remains only to deal with the signs. The multiplier $2\left(\sqrt(3)-2 \right)$ does not contain the variable $x$ - it's just a constant, and we need to figure out its sign. To do this, note the following:

\[\begin(matrix) \sqrt(3) \lt \sqrt(4)=2 \\ \Downarrow \\ 2\left(\sqrt(3)-2 \right) \lt 2\cdot \left(2 -2 \right)=0 \\\end(matrix)\]

It turns out that the second factor is not just a constant, but a negative constant! And when dividing by it, the sign of the original inequality will change to the opposite:

\[\begin(align) & \left(((x)^(2))-2x-0 \right)\cdot 2\left(\sqrt(3)-2 \right) \lt 0; \\ & ((x)^(2))-2x-0 \gt 0; \\ & x\left(x-2 \right) \gt 0. \\\end(align)\]

Now everything becomes quite obvious. The roots of the square trinomial on the right are $((x)_(1))=0$ and $((x)_(2))=2$. We mark them on the number line and look at the signs of the function $f\left(x \right)=x\left(x-2 \right)$:

The case when we are interested in lateral intervals

We are interested in the intervals marked with a plus sign. It remains only to write down the answer:

Let's move on to the next example:

\[((\left(\frac(1)(3) \right))^(((x)^(2))+2x)) \gt ((\left(\frac(1)(9) \ right))^(16-x))\]

Well, everything is quite obvious here: the bases are powers of the same number. Therefore, I will write everything briefly:

\[\begin(matrix) \frac(1)(3)=((3)^(-1));\quad \frac(1)(9)=\frac(1)(((3)^( 2)))=((3)^(-2)) \\ \Downarrow \\ ((\left(((3)^(-1)) \right))^(((x)^(2) )+2x)) \gt ((\left(((3)^(-2)) \right))^(16-x)) \\\end(matrix)\]

\[\begin(align) & ((3)^(-1\cdot \left(((x)^(2))+2x \right))) \gt ((3)^(-2\cdot \ left(16-x\right))); \\ & ((3)^(-((x)^(2))-2x)) \gt ((3)^(-32+2x)); \\ & \left(-((x)^(2))-2x-\left(-32+2x \right) \right)\cdot \left(3-1 \right) \gt 0; \\ & -((x)^(2))-2x+32-2x \gt 0; \\ & -((x)^(2))-4x+32 \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))+4x-32 \lt 0; \\ & \left(x+8 \right)\left(x-4 \right) \lt 0. \\\end(align)\]

As you can see, in the process of transformations, we had to multiply by negative number, so the inequality sign has changed. At the very end, I again applied Vieta's theorem to factorize a square trinomial. As a result, the answer will be the following: $x\in \left(-8;4 \right)$ - those who wish can verify this by drawing a number line, marking points and counting signs. In the meantime, we will move on to the last inequality from our “set”:

\[((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt 1\]

As you can see, the base is again an irrational number, and the unit is again on the right. Therefore, we rewrite our exponential inequality as follows:

\[((\left(3-2\sqrt(2) \right))^(3x-((x)^(2)))) \lt ((\left(3-2\sqrt(2) \ right))^(0))\]

Let's rationalize:

\[\begin(align) & \left(3x-((x)^(2))-0 \right)\cdot \left(3-2\sqrt(2)-1 \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot \left(2-2\sqrt(2) \right) \lt 0; \\ & \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0. \\\end(align)\ ]

However, it is quite obvious that $1-\sqrt(2) \lt 0$, since $\sqrt(2)\approx 1.4... \gt 1$. Therefore, the second factor is again a negative constant, by which both parts of the inequality can be divided:

\[\begin(matrix) \left(3x-((x)^(2))-0 \right)\cdot 2\left(1-\sqrt(2) \right) \lt 0 \\ \Downarrow \ \\end(matrix)\]

\[\begin(align) & 3x-((x)^(2))-0 \gt 0; \\ & 3x-((x)^(2)) \gt 0;\quad \left| \cdot \left(-1 \right) \right. \\ & ((x)^(2))-3x \lt 0; \\ & x\left(x-3 \right) \lt 0. \\\end(align)\]

Change to another base

A separate problem in solving exponential inequalities is the search for the “correct” basis. Unfortunately, at the first glance at the task it is far from always obvious what to take as a basis, and what to do as the degree of this basis.

But do not worry: there is no magic and "secret" technologies here. In mathematics, any skill that cannot be algorithmized can be easily developed through practice. But for this you will have to solve problems of different levels of complexity. For example, these are:

\[\begin(align) & ((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x))); \\ & ((\left(\frac(1)(3) \right))^(\frac(3)(x)))\ge ((3)^(2+x)); \\ & ((\left(0,16 \right))^(1+2x))\cdot ((\left(6,25 \right))^(x))\ge 1; \\ & ((\left(\frac(27)(\sqrt(3)) \right))^(-x)) \lt ((9)^(4-2x))\cdot 81. \\\ end(align)\]

Hard? Fearfully? Yes, it's easier than a chicken on the asphalt! Let's try. First inequality:

\[((2)^(\frac(x)(2))) \lt ((4)^(\frac(4)(x)))\]

Well, I think everything is clear here:

We rewrite the original inequality, reducing everything to the base "two":

\[((2)^(\frac(x)(2))) \lt ((2)^(\frac(8)(x)))\Rightarrow \left(\frac(x)(2)- \frac(8)(x) \right)\cdot \left(2-1 \right) \lt 0\]

Yes, yes, you understood correctly: I just applied the rationalization method described above. Now we need to work carefully: we got a fractional-rational inequality (this is one that has a variable in the denominator), so before equating something to zero, you need to reduce everything to a common denominator and get rid of the constant factor.

\[\begin(align) & \left(\frac(x)(2)-\frac(8)(x) \right)\cdot \left(2-1 \right) \lt 0; \\ & \left(\frac(((x)^(2))-16)(2x) \right)\cdot 1 \lt 0; \\ & \frac(((x)^(2))-16)(2x) \lt 0. \\\end(align)\]

Now we use the standard interval method. Numerator zeros: $x=\pm 4$. The denominator goes to zero only when $x=0$. In total, there are three points that should be marked on the number line (all points are punctured, because the inequality sign is strict). We get:

More complicated case: three roots

As you might guess, hatching marks the intervals at which the expression on the left takes negative values. Therefore, two intervals will go into the final answer at once:

The ends of the intervals are not included in the answer because the original inequality was strict. No further validation of this answer is required. In this regard, exponential inequalities are much simpler than logarithmic ones: no DPV, no restrictions, etc.

Let's move on to the next task:

\[((\left(\frac(1)(3) \right))^(\frac(3)(x)))\ge ((3)^(2+x))\]

There are no problems here either, since we already know that $\frac(1)(3)=((3)^(-1))$, so the whole inequality can be rewritten like this:

\[\begin(align) & ((\left(((3)^(-1)) \right))^(\frac(3)(x)))\ge ((3)^(2+x ))\Rightarrow ((3)^(-\frac(3)(x)))\ge ((3)^(2+x)); \\ & \left(-\frac(3)(x)-\left(2+x \right) \right)\cdot \left(3-1 \right)\ge 0; \\ & \left(-\frac(3)(x)-2-x \right)\cdot 2\ge 0;\quad \left| :\left(-2\right)\right. \\ & \frac(3)(x)+2+x\le 0; \\ & \frac(((x)^(2))+2x+3)(x)\le 0. \\\end(align)\]

Please note: in the third line, I decided not to waste time on trifles and immediately divide everything by (−2). Minul went into the first bracket (now there are pluses everywhere), and the deuce was reduced with a constant multiplier. This is exactly what you should do when making real calculations on independent and control work- no need to paint directly every action and transformation.

Next, the familiar method of intervals comes into play. Zeros of the numerator: but there are none. Because the discriminant will be negative. In turn, the denominator is set to zero only when $x=0$ — just like last time. Well, it is clear that the fraction will take positive values ​​to the right of $x=0$, and negative ones to the left. Since we are only interested in negative values, the final answer is $x\in \left(-\infty ;0 \right)$.

\[((\left(0,16 \right))^(1+2x))\cdot ((\left(6,25 \right))^(x))\ge 1\]

And what should be done with decimal fractions in exponential inequalities? That's right: get rid of them by converting them into ordinary ones. Here we are translating:

\[\begin(align) & 0,16=\frac(16)(100)=\frac(4)(25)\Rightarrow ((\left(0,16 \right))^(1+2x)) =((\left(\frac(4)(25) \right))^(1+2x)); \\ & 6,25=\frac(625)(100)=\frac(25)(4)\Rightarrow ((\left(6,25 \right))^(x))=((\left(\ frac(25)(4) \right))^(x)). \\\end(align)\]

Well, what did we get in the bases of exponential functions? And we got two mutually reciprocal numbers:

\[\frac(25)(4)=((\left(\frac(4)(25) \right))^(-1))\Rightarrow ((\left(\frac(25)(4) \ right))^(x))=((\left(((\left(\frac(4)(25) \right))^(-1)) \right))^(x))=((\ left(\frac(4)(25) \right))^(-x))\]

Thus, the original inequality can be rewritten as follows:

\[\begin(align) & ((\left(\frac(4)(25) \right))^(1+2x))\cdot ((\left(\frac(4)(25) \right) )^(-x))\ge 1; \\ & ((\left(\frac(4)(25) \right))^(1+2x+\left(-x \right)))\ge ((\left(\frac(4)(25) \right))^(0)); \\ & ((\left(\frac(4)(25) \right))^(x+1))\ge ((\left(\frac(4)(25) \right))^(0) ). \\\end(align)\]

Of course, when multiplying powers with the same base, their indicators add up, which happened in the second line. In addition, we have represented the unit on the right, also as a power in base 4/25. It remains only to rationalize:

\[((\left(\frac(4)(25) \right))^(x+1))\ge ((\left(\frac(4)(25) \right))^(0)) \Rightarrow \left(x+1-0 \right)\cdot \left(\frac(4)(25)-1 \right)\ge 0\]

Note that $\frac(4)(25)-1=\frac(4-25)(25) \lt 0$, i.e. the second factor is a negative constant, and when divided by it, the inequality sign will change:

\[\begin(align) & x+1-0\le 0\Rightarrow x\le -1; \\ & x\in \left(-\infty ;-1 \right]. \\\end(align)\]

Finally, the last inequality from the current "set":

\[((\left(\frac(27)(\sqrt(3)) \right))^(-x)) \lt ((9)^(4-2x))\cdot 81\]

In principle, the idea of ​​the solution here is also clear: all the exponential functions that make up the inequality must be reduced to the base "3". But for this you have to tinker a little with roots and degrees:

\[\begin(align) & \frac(27)(\sqrt(3))=\frac(((3)^(3)))(((3)^(\frac(1)(3)) ))=((3)^(3-\frac(1)(3)))=((3)^(\frac(8)(3))); \\ & 9=((3)^(2));\quad 81=((3)^(4)). \\\end(align)\]

Given these facts, the original inequality can be rewritten as follows:

\[\begin(align) & ((\left(((3)^(\frac(8)(3))) \right))^(-x)) \lt ((\left(((3) ^(2)) \right))^(4-2x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x))\cdot ((3)^(4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(8-4x+4)); \\ & ((3)^(-\frac(8x)(3))) \lt ((3)^(4-4x)). \\\end(align)\]

Pay attention to the 2nd and 3rd lines of calculations: before doing something with inequality, be sure to bring it to the form that we talked about from the very beginning of the lesson: $((a)^(x)) \lt ((a)^(n))$. As long as you have left or right left multipliers, extra constants, etc., no rationalization and "crossing out" of the grounds can be performed! Countless tasks have been done wrong due to a misunderstanding of this simple fact. I myself constantly observe this problem with my students, when we are just starting to analyze demonstrative and logarithmic inequalities.

But back to our task. Let's try this time to do without rationalization. Remember: the base of the degree is greater than one, so the triples can simply be crossed out - the inequality sign will not change. We get:

\[\begin(align) & -\frac(8x)(3) \lt 4-4x; \\ & 4x-\frac(8x)(3) \lt 4; \\ & \frac(4x)(3) \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end(align)\]

That's all. Final answer: $x\in \left(-\infty ;3 \right)$.

Highlighting a stable expression and replacing a variable

In conclusion, I propose to solve four more exponential inequalities, which are already quite difficult for unprepared students. To cope with them, you need to remember the rules for working with degrees. In particular, putting common factors out of brackets.

But the most important thing is to learn to understand: what exactly can be bracketed. Such an expression is called stable - it can be denoted by a new variable and thus get rid of the exponential function. So, let's look at the tasks:

\[\begin(align) & ((5)^(x+2))+((5)^(x+1))\ge 6; \\ & ((3)^(x))+((3)^(x+2))\ge 90; \\ & ((25)^(x+1,5))-((5)^(2x+2)) \gt 2500; \\ & ((\left(0,5 \right))^(-4x-8))-((16)^(x+1,5)) \gt 768. \\\end(align)\]

Let's start with the very first line. Let's write this inequality separately:

\[((5)^(x+2))+((5)^(x+1))\ge 6\]

Note that $((5)^(x+2))=((5)^(x+1+1))=((5)^(x+1))\cdot 5$, so the right side can be rewrite:

Note that there are no other exponential functions except for $((5)^(x+1))$ in the inequality. And in general, the variable $x$ does not occur anywhere else, so let's introduce a new variable: $((5)^(x+1))=t$. We get the following construction:

\[\begin(align) & 5t+t\ge 6; \\ & 6t\ge 6; \\ & t\ge 1. \\\end(align)\]

We return to the original variable ($t=((5)^(x+1))$), and at the same time remember that 1=5 0 . We have:

\[\begin(align) & ((5)^(x+1))\ge ((5)^(0)); \\ &x+1\ge 0; \\ & x\ge -1. \\\end(align)\]

That's the whole solution! Answer: $x\in \left[ -1;+\infty \right)$. Let's move on to the second inequality:

\[((3)^(x))+((3)^(x+2))\ge 90\]

Everything is the same here. Note that $((3)^(x+2))=((3)^(x))\cdot ((3)^(2))=9\cdot ((3)^(x))$ . Then the left side can be rewritten:

\[\begin(align) & ((3)^(x))+9\cdot ((3)^(x))\ge 90;\quad \left| ((3)^(x))=t \right. \\&t+9t\ge 90; \\ & 10t\ge 90; \\ & t\ge 9\Rightarrow ((3)^(x))\ge 9\Rightarrow ((3)^(x))\ge ((3)^(2)); \\ & x\ge 2\Rightarrow x\in \left[ 2;+\infty \right). \\\end(align)\]

This is approximately how you need to draw up a decision on real control and independent work.

Well, let's try something more difficult. For example, here is an inequality:

\[((25)^(x+1,5))-((5)^(2x+2)) \gt 2500\]

What is the problem here? First of all, the bases of the exponential functions on the left are different: 5 and 25. However, 25 \u003d 5 2, so the first term can be transformed:

\[\begin(align) & ((25)^(x+1,5))=((\left(((5)^(2)) \right))^(x+1,5))= ((5)^(2x+3)); \\ & ((5)^(2x+3))=((5)^(2x+2+1))=((5)^(2x+2))\cdot 5. \\\end(align )\]

As you can see, at first we brought everything to the same base, and then we noticed that the first term is easily reduced to the second - it is enough just to expand the exponent. Now we can safely introduce a new variable: $((5)^(2x+2))=t$, and the whole inequality will be rewritten like this:

\[\begin(align) & 5t-t\ge 2500; \\ & 4t\ge 2500; \\ & t\ge 625=((5)^(4)); \\ & ((5)^(2x+2))\ge ((5)^(4)); \\ & 2x+2\ge 4; \\ & 2x\ge 2; \\ & x\ge 1. \\\end(align)\]

Again, no problem! Final answer: $x\in \left[ 1;+\infty \right)$. Moving on to the final inequality in today's lesson:

\[((\left(0,5 \right))^(-4x-8))-((16)^(x+1,5)) \gt 768\]

The first thing to note is, of course, decimal at the base of the first degree. It is necessary to get rid of it, and at the same time bring all exponential functions to the same base - the number "2":

\[\begin(align) & 0,5=\frac(1)(2)=((2)^(-1))\Rightarrow ((\left(0,5 \right))^(-4x- 8))=((\left(((2)^(-1)) \right))^(-4x-8))=((2)^(4x+8)); \\ & 16=((2)^(4))\Rightarrow ((16)^(x+1,5))=((\left(((2)^(4)) \right))^( x+1.5))=((2)^(4x+6)); \\ & ((2)^(4x+8))-((2)^(4x+6)) \gt 768. \\\end(align)\]

Great, we have taken the first step - everything has led to the same foundation. Now we need to highlight set expression. Note that $((2)^(4x+8))=((2)^(4x+6+2))=((2)^(4x+6))\cdot 4$. If we introduce a new variable $((2)^(4x+6))=t$, then the original inequality can be rewritten as follows:

\[\begin(align) & 4t-t \gt 768; \\ & 3t \gt 768; \\ & t \gt 256=((2)^(8)); \\ & ((2)^(4x+6)) \gt ((2)^(8)); \\ & 4x+6 \gt 8; \\ & 4x \gt 2; \\ & x \gt \frac(1)(2)=0.5. \\\end(align)\]

Naturally, the question may arise: how did we find out that 256 = 2 8 ? Unfortunately, here you just need to know the powers of two (and at the same time the powers of three and five). Well, or divide 256 by 2 (you can divide, since 256 is an even number) until we get the result. It will look something like this:

\[\begin(align) & 256=128\cdot 2= \\ & =64\cdot 2\cdot 2= \\ & =32\cdot 2\cdot 2\cdot 2= \\ & =16\cdot 2 \cdot 2\cdot 2\cdot 2= \\ & =8\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =4\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =((2)^(8)).\end(align )\]

The same is with the three (numbers 9, 27, 81 and 243 are its powers), and with the seven (numbers 49 and 343 would also be nice to remember). Well, the five also have “beautiful” degrees that you need to know:

\[\begin(align) & ((5)^(2))=25; \\ & ((5)^(3))=125; \\ & ((5)^(4))=625; \\ & ((5)^(5))=3125. \\\end(align)\]

Of course, if you wish, all these numbers can be restored in your mind by simply multiplying them one by one. However, when you have to solve several exponential inequalities, and each next one is more difficult than the previous one, then the last thing you want to think about is the powers of some numbers there. And in this sense, these problems are more complex than the "classical" inequalities, which are solved by the interval method.

I hope this lesson helped you in mastering this topic. If something is not clear, ask in the comments. And see you in the next tutorials. :)

Mathematics teacher MOU - secondary school No. 2 r.p. Stepnoe Trufyakova Galina Ivanovna website

slide 2

Lesson summary

The topic "Exponatory inequalities" is the most important topic in mathematics. According to the textbook by S. M. Nikolsky, it is studied in the 10th grade and 2 hours are allotted for its study in planning: 1 hour - The simplest exponential inequalities; 1 hour - Inequalities that are reduced to the simplest replacement of the unknown. During this time, it is necessary to introduce students to new and very voluminous material, teach them to solve all types of exponential inequalities and develop these skills and abilities well. Therefore, lessons in the formation of new knowledge in the form of lectures using information and communication technology allow solving these problems quickly and with great success.

slide 3

slide 4

Albert Einstein

“I have to divide my time between politics and solving equations and inequalities. However, the solution of equations and inequalities, in my opinion, is much more important, because politics exists only for this moment, and equations and inequalities will exist forever.

slide 5

Lesson structure

Organizing time Setting goals and objectives Lecture plan Actualization of students' knowledge in the form of repetition of previously studied material Introduction of new knowledge Consolidation of knowledge in the form of an interview Summing up the lesson Homework

slide 6

Organizing time

Greet students Record the names of students who are absent from class in the class journal

Slide 7

Setting goals and objectives

Announce to students at the beginning of the lesson its goals and objectives Introduce students to the lecture plan and write it down in a notebook

Slide 8

Lesson Objectives

Educational Formation of the concept of exponential inequality Familiarization of students with types of exponential inequalities Formation of skills and abilities to solve exponential inequalities

Slide 9

Educational Education of industriousness Education of independence in achieving the goal Formation of computational skills Formation of aesthetic skills when making notes

Slide 10

Developing Development of mental activity Development of creative initiative Development of cognitive activity Development of speech and memory

slide 11

Lesson objectives

Repeat the properties of an exponential function Repeat the rules for solving square and fractionally rational inequalities Work out an algorithm for solving the simplest exponential inequalities Teach students to distinguish between types of exponential inequalities Teach students to solve exponential inequalities

slide 12

Lesson type

Lesson in the formation of new knowledge

slide 13

Type of lesson

Lesson - lecture

Slide 14

Teaching methods

Explanatory-illustrative Heuristic Search Problematic

slide 15

Learning technology

Information and Communication Technology Based on Problem-Based Learning

slide 16

Lecture plan

Repetition of the properties of an exponential function The simplest exponential inequalities The exponential inequalities that reduce to the simplest ones The exponential inequalities that reduce to quadratic inequalities Homogeneous exponential inequalities of the first degree Homogeneous exponential inequalities of the second degree Exponential inequalities that reduce to rational inequalities Exponential non-standard inequalities

Slide 17

Repetition of previously studied material

Solve on the board and in notebooks: a) square inequalities: x² - 2x - 1≥0 x² - 2x - 3 ≤0 b) fractional-rational inequality: (x - 5) \ (x - 2) ≤ 0

Slide 18

Repetition of the properties of the exponential function

Slide 19

monotonically decreasing on R The x-axis is a horizontal asymptote monotonically increasing on R 8. For any real values ​​of x and y; a>0, a≠1; b>0, b≠1. 7. Asymptote 6. Extrema 5. Monotonicity 4. Even, odd 3. Intervals of comparison of values ​​of a function with unity 2. Range of values ​​of a function 1 Domain of a function Properties of an exponential function Exponential inequalities, their types and methods of solution Exponential function has no extremums The function is neither even nor odd (general function).

Slide 20

Exponential inequalities, their types and methods of solution Task number 1 Find the domain of the function

slide 21

Exponential inequalities, their types and methods of solution Task number 2 Determine the values

slide 22

Exponential inequalities, their types and methods of solution Task № 3 Determine the type of function increasing decreasing increasing decreasing

slide 23

Introduction of new knowledge

slide 24

Exponential inequalities, their types and methods of solution DEFINITION of the simplest exponential inequalities: Let a be a given positive number not equal to one and b be a given real number. Then the inequalities ax>b (ax≥b) and ax

Slide 25

Exponential inequalities, their types and methods of solution The solution of an inequality with unknown x is the number x0, when substituting it into the inequality, a true numerical inequality is obtained.

Slide 26

Exponential inequalities, their types and methods of solution WHAT DOES IT MEAN to solve an inequality? To solve an inequality means to find all its solutions or show that there are none.

Slide 27

Consider the relative position of the graph of the function y=ax, a>0, a≠1 and the straight line y=b. Exponential inequalities, their types and methods for solving y x y x y=b, b 0 y=b, b>0 0 1 0 1 x0 x0

Slide 28

Exponential inequalities, their types and methods of solution is located below the curve y=ax, so the inequalities ax>b(ax≥b) hold for xR, and the inequalities ax

Slide 29

CONCLUSION №2: y x ​​0 x0 x1 y=b, b>0 x2 Exponential inequalities, their types and methods of solution If a>1 and b > 0, then for each x1 x0- below the line y=b. 1 For b> 0, the line y = b intersects the graph of the function y= ax at a single point, the abscissa of which is x0 = logab

slide 30

CONCLUSION №2: yx 0 x0 x1 y=b, b>0 1 Exponential inequalities, their types and methods of solution of each x2 0, the line y = b intersects the graph of the function y= ax at a single point, the abscissa of which is x0 = logab x2

Slide 31

The simplest exponential inequalities Exponential inequalities, their types and methods of solution

slide 32

Exponential inequalities, their types and solution methods Example No. 1.1 Answer: increases over the entire domain of definition, Solution:

Slide 33

Exponential inequalities, their types and solution methods Example No. 1.2 Solution: Answer: decreases over the entire domain of definition,

slide 34

Exponential inequalities, their types and solution methods Example No. 1.3 Solution: Answer: increases throughout the entire domain of definition,

Slide 35

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them

slide 36

Exponential inequalities, their types and solution methods Example No. 1.4 Solution: increases over the entire domain of definition, Answer:

Slide 37

Exponential inequalities, their types and solution methods

Slide 38

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them 2) Exponential inequalities that reduce to quadratic inequalities

Slide 39

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them 3) Homogeneous exponential inequalities of the first and second degree. Homogeneous exponential inequalities of the first degree Example No. 1 increases over the entire domain of definition Answer: Solution:

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them 4) Exponential inequalities that reduce to rational inequalities

slide 43

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them 5) Exponential non-standard inequalities Example Solution: Let's solve each statement of the set separately. Inequality equals aggregate

Slide 44

Exponential inequalities, their types and methods for solving Types of exponential inequalities and methods for solving them is not a solution to the equation. So,

Slide 45

Consolidation of knowledge

What inequalities are called exponential? When does an exponential inequality have a solution for any values ​​of x? When does an exponential inequality have no solutions? What types of inequalities did you learn in this lesson? How are simple inequalities solved? How are inequalities reduced to square ones solved? How are homogeneous inequalities solved? How are inequalities reduced to rational ones solved?

Slide 46

Lesson summary

Find out what students have learned in this lesson Assign marks to students for work in the lesson with detailed commentary

Slide 47

Homework

Textbook for grade 10 "Algebra and the beginning of analysis" author S.M. Nikolsky To study paragraphs 6.4 and 6.6, No. 6.31-6.35 and No. 6.45-6.50 solve

Slide 48

Exponential inequalities, their types and methods of solution

Algebra and beginnings mathematical analysis. Grade 10. Textbook. Nikolsky S.M. and etc.

Basic and profile levels

8th ed. - M.: Enlightenment, 2009. - 430 p.

The textbook complies with the federal components of the state standard general education in mathematics and contains material for both basic and profile level. You can work on it regardless of what textbooks students studied in previous years.

The textbook is aimed at preparing students for admission to universities.

Format: djvu

The size: 15.2 MB

Watch, download:drive.google ; Rghost

Format: pdf

The size: 42.3 MB

Watch, download:drive.google ; Rghost

Note: In PDF, the quality is better, almost excellent. Made from the same scan, 150 dpi, color. But in DJVU it turns out a little worse. This is one case where size matters.

TABLE OF CONTENTS
CHAPTER I. ROOTS, POWERS, LOGARITHS
§ 1. Real numbers 3
1.1. The concept of a real number 3
1.2. Sets of numbers. Properties of real numbers. ... 10
1.3*. Method of mathematical induction 16
1.4. Permutations 22
1.5. Accommodations 25
1.6. Combinations 27
1.7*. Proof of numerical inequalities 30
1.8*. Divisibility of integers 35
1.9*. Comparisons modulo m 38
1.10*. Problems with integer unknowns 40
§ 2. Rational equations and inequalities 44
2.1. Rational Expressions 44
2.2. Newton's binomial formulas, sums and differences of degrees. . 48
2.3*. Division of polynomials with remainder. Euclid's algorithm... 53
2.4*. Bezout's theorem 57
2.5*. Polynomial root 60
2.6. Rational equations 65
2.7. Systems of rational equations 70
2.8. Method of intervals for solving inequalities 75
2.9. Rational inequalities 79
2.10. Non-strict inequalities 84
2.11. Systems of rational inequalities 88
§ 3. Root of degree n 93
3.1. The concept of a function and its graph 93
3.2. Function y \u003d x "96
3.3. The concept of the root of the degree n 100
3.4. Roots of even and odd powers 102
3.5. Arithmetic root 106
3.6. Properties of roots of degree l 111
3.7*. Function y \u003d nx (x\u003e 0) 114
3.8*. Function y = nVx 117
3.9*. n root of natural number 119
§ 4. Power of a positive number 122
4.1. Degree c rational indicator 122
4.2. Power properties with rational exponent 125
4.3. The concept of the limit of a sequence 131
4.4*. Limit Properties 134
4.5. Infinitely decreasing geometric progression. . . 137
4.6. Number e 140
4.7. The concept of degree with an irrational exponent .... 142
4.8. exponential function 144
§ 5. Logarithms 148
5.1. The concept of the logarithm 148
5.2. Properties of logarithms 151
5.3. Logarithmic function 155
5.4*. Decimal logarithms 157
5.5*. Power functions 159
§ 6. Demonstrative and logarithmic equations and inequalities. . 164
6.1. The simplest exponential equations 164
6.2. The simplest logarithmic equations 166
6.3. Equations reduced to the simplest by changing the unknown 169
6.4. The simplest exponential inequalities 173
6.5. The simplest logarithmic inequalities 178
6.6. Inequalities Reducing to the Simplest Substitution of the Unknown 182
Historical information 187
CHAPTER II. TRIGONOMETRIC FORMULA. TRIGONOMETRIC FUNCTIONS
§ 7. Sine and cosine of an angle 193
7.1. The concept of angle 193
7.2. Radian measure of an angle 200
7.3. Determining the sine and cosine of an angle 203
7.4. Basic formulas for sin a and cos a 211
7.5. Arcsine 216
7.6. Arc cosine 221
7.7*. Examples of using arcsine and arccosine .... 225
7.8*. Formulas for Arcsine and Arccosine 231
§ 8. Tangent and cotangent of an angle 233
8.1. Determining the tangent and cotangent of an angle 233
8.2. Basic formulas for tg a and ctg a 239
8.3. Arctangent 243
8.4*. Arc tangent 246
8.5*. Examples of using arc tangent and arc tangent. . 249
8.6*. Formulas for arc tangent and arc tangent 255
§ 9. Addition formulas 258
9.1. Cosine of the difference and cosine of the sum of two angles 258
9.2. Formulas for Complementary Angles 262
9.3. Sine of the sum and sine of the difference of two angles 264
9.4. Sum and difference of sines and cosines 266
9.5. Formulas for double and half angles 268
9.6*. Product of sines and cosines 273
9.7*. Formulas for tangents 275
§ 10. Trigonometric functions numeric argument 280
10.1. Function y \u003d sin x 281
10.2. Function y \u003d cos x 285
10.3. Function y = tg * 288
10.4. Function y = ctg x 292
§ 11. Trigonometric equations and inequalities 295
11.1. The simplest trigonometric equations 295
11.2. Equations Reducing to the Simplest by Replacing the Unknown 299
11.3. Application of basic trigonometric formulas for solving equations 303
11.4. Homogeneous equations 307
11.5*. The simplest inequalities for sine and cosine .... 310
11.6*. The simplest inequalities for tangent and cotangent. . . 315
11.7*. Inequalities Reducing to the Simplest Substitution of the Unknown 319
11.8*. Introduction of the auxiliary angle 322
11.9*. Replacing the unknown t \u003d sin x + cos x 327
Historical information 330
CHAPTER III. ELEMENTS OF PROBABILITY THEORY
§ 12. Probability of an event 333
12.1. The concept of the probability of an event 333
12.2. Properties of event probabilities 338
§ thirteen*. Frequency. Conditional Probability 342
13.1*. Relative event frequency 342
13.2*. Conditional Probability. Independent events 344
§ 14*. Expected value. Law of Large Numbers 348
14.1*. Mathematical expectation 348
14.2*. Difficult experience 353
14.3*. Bernoulli formula. Law of Large Numbers 355
Historical information 359
REVIEW 362
Index 407
Answers 410

Topic 6. Exponential and logarithmic equations and inequalities (11 hours)
Lesson topic. Inequalities that are reduced to the simplest by replacing the unknown.
The purpose of the lesson: To form the skills of solving exponential and logarithmic inequalities, by reducing to the simplest ones, by replacing the unknown.
Tasks:
Educational: repeat and consolidate knowledge on the topic "solving the simplest exponential and logarithmic inequalities", learn how to solve logarithmic and exponential inequalities by the replacement method.
Developing: to form the student's ability to distinguish two types of inequality and determine ways to solve them (logical and intuitive thinking, substantiation of judgments, classification, comparison), to form skills of self-control and self-examination, the ability to move according to a given algorithm, evaluate and correct the result.
Educational: to continue the formation of such qualities of students as: the ability to listen to each other; the ability to exercise mutual control and self-assessment.
Lesson type: combined.
Textbook Algebra Grade 10 S.M. Nikolsky, M.K. Potapov, N.N. Reshetnikov, A.V. Shevkin
During the classes
Organizing time.
Checking homework.
Updating of basic knowledge.
Frontal:
1. What inequalities are called the simplest exponential inequalities?
2. Explain what is the meaning of solving the simplest exponential inequalities.
3. What inequalities are called the simplest logarithmic inequalities?
4. Explain what is the meaning of solving the simplest logarithmic inequalities.
With a note on the board (1 student each):
Solve inequalities
2x<1160,3х<103log2x>5log15x>-2Explanation of the new material and its gradual consolidation.
1.1. Explanation of new material.
1. Solve the inequality:
2x2-3x<14Пусть х2-3х=t, тогда
2t<142t<2-2т. к. основание 2>1, then
t<-2Обратная замена:
x2-3x<-2х2-3х+2<0Нахдим его корни: x1=1, x2=2Отмечаем эти точки на координатной прямой и выясняем знак выражения x2−3x+2 на каждом из полученных интервалов.
We are interested in the sign "−−". Then we get
Answer:x∈(1;2)
2. Solve the inequality

1.2. Step by step reinforcement.
No. 6.49(a, c).
No. 6.52(e).
a) 74x2-9x+6>74x2-9x+6>14x2-9x+5>0x1=5/4 x2=1
Answer: -∞; 1∪54; + ∞v) (13) 5x2-4x-3> 95x2-4x-3<-25х2-4х-1<0x1=-15 x2=1
Answer: -15; 1e) log5x2-2x-3<1
log5x2-2x-3 00<х2-2х-3<5х2-2х-3<5х2-2х-3>0 x2-2x-8<0х2-2х-3>0

Answer: -2;-1∪3;42.1. Explanation of new material.
3. Solve the inequality

Then 1 inequality makes sense for all x, and the second

2.2. Step by step reinforcement.
Solve inequality #6.56(c)
3.1. Explanation of new material.
4. Solve the inequality

3.2. Step by step reinforcement.
Solve inequality #6.60(a)
Summing up the lesson.
Reflection.
Homework.
P. 6.6
No. 6.49 (b, d)
No. 6.52 (a, b)
No. 6.56 (d)
No. 6.60 (b)

Attached files