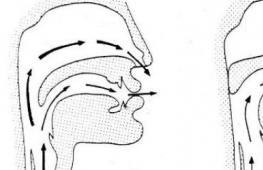
Jäiga keha pöörlemistelg. Jäiga keha pöörlev liikumine ümber fikseeritud telje
See artikkel kirjeldab olulist füüsika osa - "Pöörleva liikumise kinemaatika ja dünaamika".
Pöörleva liikumise kinemaatika põhimõisted
Materiaalse punkti pöörlev liikumine ümber fikseeritud telje on selline liikumine, mille trajektooriks on ringjoon, mis asub teljega risti asetseval tasapinnal ja mille kese asub pöörlemisteljel.
Jäiga keha pöörlev liikumine on liikumine, mille käigus kõik keha punktid liiguvad mööda kontsentrilisi (mille keskpunktid asuvad samal teljel) ringjooni vastavalt materiaalse punkti pöörleva liikumise reeglile.
Laske suvalisel jäigal kehal T sooritada pöördeid ümber joonise tasapinnaga risti asetseva telje O. Valime antud kehal punkti M. Pöörlemisel kirjeldab see punkt O-telje ümber raadiusega ringi. r.
Mõne aja pärast pöördub raadius algse asukoha suhtes nurga Δφ võrra.
Positiivseks pöörlemissuunaks võetakse parempoolse kruvi suund (päripäeva). Pöörlemisnurga muutumist ajaga nimetatakse jäiga keha pöörlemisliikumise võrrandiks:
φ = φ(t).
Kui φ mõõdetakse radiaanides (1 rad on nurk, mis vastab kaarele, mille pikkus on võrdne selle raadiusega), siis ringkaare ΔS pikkus, mille materiaalne punkt M läbib ajas Δt, on võrdne:
∆S = ∆φr.
Ühtlase pöörleva liikumise kinemaatika põhielemendid
Materiaalse punkti liikumise mõõt lühikese aja jooksul dt toimib elementaarse pöörlemisvektorina dφ.
Materiaalse punkti või keha nurkkiirus on füüsiline kogus, mille määrab elementaarpöörde vektori ja selle pöörde kestuse suhe. Vektori suuna saab määrata piki O-telge parema kruvi reegliga Skalaarsel kujul:
ω = dφ/dt.
Kui ω = dφ/dt = konst, siis sellist liikumist nimetatakse ühtlaseks pöörlevaks liikumiseks. Sellega määratakse nurkkiirus valemiga
ω = φ/t.
Eelvalemi järgi nurkkiiruse mõõde
[ω] = 1 rad/s.
Keha ühtlast pöörlevat liikumist saab kirjeldada pöörlemisperioodiga. Pöörlemisperiood T on füüsikaline suurus, mis määrab aja, mis kulub kehal ühe täispöörde sooritamiseks ümber pöörlemistelje ([T] = 1 s). Kui nurkkiiruse valemis võtame t = T, φ = 2 π (täis üks pööre raadiusega r), siis
ω = 2π/T,
Seetõttu määratakse rotatsiooniperiood järgmiselt:
T = 2π/ω.
Pöörete arvu, mida keha teeb ajaühikus, nimetatakse pöörlemissageduseks ν, mis on võrdne:
ν = 1/T.
Sagedusühikud: [ν] \u003d 1 / c \u003d 1 c -1 \u003d 1 Hz.
Võrreldes nurkkiiruse ja pöörlemissageduse valemeid, saame neid suurusi seostava avaldise:
ω = 2πν.
Ebaühtlase pöörleva liikumise kinemaatika põhielemendid
Jäiga keha või materiaalse punkti ebaühtlane pöörlemine ümber fikseeritud telje iseloomustab selle nurkkiirust, mis ajas muutub.
Vektor ε nurkkiiruse muutumise kiirust iseloomustavat nurkiirendusvektorit nimetatakse:
ε = dω/dt.
Kui keha pöörleb, kiirendades, see tähendab dω/dt > 0, on vektoril suund piki telge samas suunas kui ω.
Kui pöörlemisliikumine on aeglustunud - dω/dt< 0 , siis on vektorid ε ja ω vastassuunalised.
kommenteerida. Kui toimub ebaühtlane pöörlev liikumine, võib vektor ω muutuda mitte ainult suuruses, vaid ka suunas (kui pöörlemistelg on pööratud).
Translatsioonilist ja pöörlevat liikumist iseloomustavate suuruste seos
On teada, et kaare pikkus raadiuse pöördenurga ja selle väärtusega on seotud seosega
∆S = ∆φr.
Siis pöörlevat liikumist sooritava materiaalse punkti lineaarkiirus
υ = ΔS/Δt = Δφr/Δt = ωr.
Pöörlevat translatsioonilist liikumist teostava materiaalse punkti normaalne kiirendus on määratletud järgmiselt:
a = υ 2 /r = ω 2 r 2 /r.
Niisiis, skalaarsel kujul
a = ω 2 r.
Tangentsiaalselt kiirendatud materjalipunkt, mis teostab pöörlevat liikumist
a = εr.
Materiaalse punkti nurkmoment
Materiaalse punkti massiga m i trajektoori raadiuse-vektori vektorkorrutist ja selle impulsi nimetatakse selle punkti nurkimpulssiks ümber pöörlemistelje. Vektori suunda saab määrata õige kruvireegli abil.
Materiaalse punkti nurkmoment ( L i) on suunatud risti läbi r i ja υ i tõmmatud tasapinnaga ning moodustab nendega vektorite parempoolse kolmiku (st vektori lõpust liikudes r i juurde υ i parempoolne kruvi näitab vektori suunda L i).
Skalaarses vormis
L = m i υ i r i sin(υ i, r i).
Arvestades, et ringjoonel liikudes on raadiuse vektor ja vektor lineaarne kiirus jaoks i-s materjal punktid on üksteisega risti,
sin(υ i , r i) = 1.
Seega saab pöörleva liikumise jaoks vajaliku materiaalse punkti nurkimment kuju
L = m i υ i r i.
i-ndale materiaalsele punktile mõjuv jõumoment
Raadiuse-vektori vektorkorrutist, mis on tõmmatud jõu rakenduspunkti, nimetatakse selle jõu mõjul mõjuva jõu momendiks. i-s materjal punkt ümber pöörlemistelje.
Skalaarses vormis
M i = r i F i sin(r i, F i).
Võttes seda arvesse r i sinα = l i ,M i = l i F i.
Väärtus l i , mis võrdub pöörlemispunktist jõu suunas langenud risti pikkusega, nimetatakse jõu haruks F i.
Pöörlemise dünaamika
Pöörleva liikumise dünaamika võrrand on kirjutatud järgmiselt:
M = dl/dt.
Seaduse sõnastus on järgmine: ümber fikseeritud telje pöörleva keha nurkimpulsi muutumise kiirus on võrdne kõigi kehale mõjuvate välisjõudude momendiga selle telje ümber.
Moment ja inertsimoment
On teada, et i-nda materiaalse punkti jaoks on nurkimpulss skalaarkujul antud valemiga
L i = m i υ i r i.
Kui lineaarkiiruse asemel asendame selle avaldise nurkkiirusega:
υ i = ωr i,
siis võtab nurkmomendi avaldis kuju
L i = m i r i 2 ω.
Väärtus I i = m i r i 2 nimetatakse inertsmomendiks umbes teljed i-ndad absoluutselt jäiga keha materiaalne punkt, mis läbib selle massikeskme. Seejärel kirjutame materiaalse punkti nurkimpulsi:
L i = I i ω.
Absoluutselt jäiga keha nurkimpulsi kirjutame nurkimpulsi summaks materiaalsed punktid mis moodustavad selle keha:
L = Iω.
Jõumoment ja inertsimoment
Pöörlemise seadus ütleb:
M = dl/dt.
On teada, et keha nurkmomenti saab esitada inertsmomendi kaudu:
L = Iω.
M = Idω/dt.
Arvestades, et nurkkiirenduse määrab avaldis
ε = dω/dt,
saame jõumomendi valemi, mis on esitatud inertsmomendi kaudu:
M = Ie.
kommenteerida. Jõumoment loetakse positiivseks, kui nurkkiirendus, millega see tekib, on suurem kui null ja vastupidi.
Steineri teoreem. Inertsimomentide liitmise seadus
Kui keha pöörlemistelg ei läbi selle massikeskpunkti, saab selle inertsimomendi selle telje suhtes leida Steineri teoreemi abil:
I \u003d I 0 + ma 2,
kus ma 0- keha alginertsimoment; m- kehamass; a- telgede vaheline kaugus.
Kui ümber fikseeritud telje pöörlev süsteem koosneb n kehad, siis on seda tüüpi süsteemi koguinertsimoment on võrdne summaga momendid, selle komponendid (inertsimomentide liitmise seadus).
pöörlev nad nimetavad sellist liikumist, mille puhul kaks kehaga ühendatud punkti, seega ja neid punkte läbiv sirgjoon, jäävad liikumise ajal liikumatuks (joon. 2.16). Fikseeritud liin A B helistas pöörlemistelg.
Riis. 2.1B. Keha pöörleva liikumise definitsiooni juurde
Keha asend pöördliikumise ajal määrab pöördenurga φ, rad (vt joon. 2.16). Liikumisel muutub pöördenurk ajaga, s.t. keha pöörlemisliikumise seadus on defineeritud kui fikseeritud pooltasandi vahelise kahetahulise nurga Φ = φ(/) aja muutumise seadus TO () , läbib pöörlemistelge ja on liigutatav lk 1 pooltasand, mis on seotud kehaga ja läbib ka pöörlemistelge.
Keha kõigi punktide trajektoorid pöördliikumise ajal on kontsentrilised ringid, mis paiknevad paralleelsel tasapinnal, mille keskpunktid on pöörlemisteljel.
Keha pöörleva liikumise kinemaatilised omadused. Sarnaselt sellele, kuidas punkti kinemaatilisi karakteristikuid tutvustati, võetakse kasutusele kinemaatiline mõiste, mis iseloomustab keha asendit pöördliikumise ajal määrava funktsiooni f(c) muutumiskiirust, s.t. nurkkiirus ω = φ = s/f/s//, nurkkiiruse mõõde [ω] = rad /alates.
Tehnilistes arvutustes kasutatakse nurkkiiruse väljendit sageli erineva mõõtmega - läbi pöörete arvu minutis: [i] = rpm ja seose P ja w võib esitada järgmiselt: w = 27sh/60 = 7sh/30.
Üldiselt muutub nurkkiirus aja jooksul. Nurkkiiruse muutumise kiiruse mõõduks on nurkkiirendus e = c/co/c//= co = f, nurkkiirenduse mõõde on [e] = rad/s 2 .
Kasutusele võetud nurkkinemaatilised karakteristikud määratakse täielikult kindlaks ühe funktsiooni seadmisega - pöördenurk ajast.
Keha punktide kinemaatilised omadused pöörleva liikumise ajal. Mõelge punktile M keha, mis asub pöörlemisteljest kaugusel p. See punkt liigub mööda ringi raadiusega p (joonis 2.17).
Riis. 2.17.
keha punktid selle pöörlemise ajal
Kaare pikkus M Q M raadiusega p ring on määratletud kui s= ptp, kus φ on pöördenurk, rad. Kui keha liikumisseadus on antud kujul φ = φ(r), siis punkti liikumisseadus M piki trajektoori määratleb valemi S= rf(7).
Kasutades kinemaatiliste karakteristikute avaldisi punkti liikumise määramise loomulikul viisil, saame pöörleva keha punktide kinemaatilised karakteristikud: kiirus vastavalt valemile (2.6)
V= 5 = rf = pco; (2.22)
tangentsiaalne kiirendus vastavalt avaldisele (2.12)
i t \u003d K \u003d wor \u003d ep; (2.23)
normaalne kiirendus vastavalt valemile (2.13)
a„ = Ja 2 / p \u003d co 2 p 2 / p \u003d ogr; (2.24)
täiskiirendus, kasutades avaldist (2.15)
aga = -]aga + a] = px/e 2 + co 4 . (2,25)
Täiskiirenduse suuna tunnusena võetakse p - täiskiirenduse vektori kõrvalekalde nurk punktiga kirjeldatud ringi raadiusest (joon. 2.18).
Jooniselt fig. 2.18 saame
tgjLi = ajan\u003d re / pco 2 \u003d g / (o 2. (2.26)
Riis. 2.18.
Pange tähele, et kõik pöörleva keha punktide kinemaatilised omadused on võrdelised kaugustega pöörlemisteljest. Ve-
Nende maskid määratakse sama funktsiooni – pöördenurga – tuletistega.
Nurga- ja lineaarkinemaatiliste karakteristikute vektoravaldised. Pöörleva keha nurkkinemaatiliste karakteristikute analüütiliseks kirjeldamiseks koos pöörlemisteljega võetakse kasutusele mõiste pöördenurga vektor(Joon. 2.19): φ = φ(/)A:, kus juurde- mine
pöörlemistelje vektor
1; juurde= con51 .
Vektor φ on suunatud piki seda telge nii, et seda saab näha "otsast"
vastupäeva pöörlemine.
Riis. 2.19.
omadused vektorkujul
Kui vektor φ(/) on teada, saab kõiki teisi pöörleva liikumise nurkkarakteristikuid esitada vektorkujul:
- nurkkiiruse vektor ω = φ = φ juurde. Nurkkiiruse vektori suund määrab pöördenurga tuletise märgi;
- nurkkiirenduse vektor є = ω = φ juurde. Selle vektori suund määrab nurkkiiruse tuletise märgi.
Kasutusele võetud vektorid co ja є võimaldavad saada vektoravaldisi punktide kinemaatiliste karakteristikute jaoks (vt joonis 2.19).
Pange tähele, et punkti kiirusvektori moodul on sama, mis moodul vektorprodukt nurkkiiruse vektor ja raadiuse vektor: |cox G= sogvipa = sor. Arvestades vektorite ω ja r suundi ning ristkorrutise suuna reeglit, saame kirjutada kiirusvektori avaldise:
V= co xg.
Samamoodi on seda lihtne näidata
- ? X
- - nt Bipa= єр = a t Ja
Sosor = co p = i.
(Lisaks sellele langevad nende kinemaatikaomaduste vektorid suunalt kokku vastavate vektoriproduktidega.
Seetõttu saab tangentsiaal- ja normaalkiirenduse vektoreid esitada vektorkorrutistena:
- (2.28)
- (2.29)
a x = z X G
aga= co x v.
Tõlkeline nimetatakse jäiga keha sellist liikumist, mille korral mis tahes sirgjoon, mis on alati selle kehaga seotud, jääb paralleelseks oma algpositsiooniga.
Teoreem. Jäiga keha translatsioonilises liikumises kirjeldavad kõik selle punktid samu trajektoore ning neil on igal hetkel võrdsed kiirused ja kiirendused nii suuruses kui suunas.
Tõestus. Läbida kaks punkti ja 
, translatsiooniliselt liikuv kehasegment 
ja arvestage selle segmendi liikumist positsioonis 
. Samas punkt 
kirjeldab trajektoori 
, ja punkt 
- trajektoor 
(joonis 56).
Arvestades, et segment 
liigub endaga paralleelselt ja selle pikkus ei muutu, saab kindlaks teha, et punktide trajektoorid 
Ja 
saab olema sama. Seega on teoreemi esimene osa tõestatud. Määrame punktide asukoha 
Ja 
vektorlikul viisil fikseeritud alguspunkti suhtes 
. Samal ajal on need raadiused - vektorid sõltuvad 
. Sest. ei lõigu pikkus ega suund 
ei muutu keha liikumisel, siis vektor 
. Jätkame kiiruste määramisega sõltuvuse (24) järgi:
, saame 
.
Jätkame kiirenduste määramisega sõltuvuse järgi (26):
, saame 
.
Tõestatud teoreemist järeldub, et keha translatsiooniline liikumine on täielikult määratud, kui on teada vaid ühe mõne punkti liikumine. Seetõttu uuring edasi liikumine jäiga keha kohta taandatakse selle ühe punkti liikumise uurimisele, s.o. punkti kinemaatika probleemile.
Teema 11. Jäiga keha pöörlev liikumine
pöörlev on jäiga keha selline liikumine, mille kaks punkti jäävad liikumatuks kogu liikumisaja jooksul. Neid kahte fikseeritud punkti läbivat sirget nimetatakse pöörlemistelg.
Iga keha punkt, mis ei asu sellise liikumise ajal pöörlemisteljel, kirjeldab ringi, mille tasapind on pöörlemisteljega risti ja selle kese asub sellel teljel.
Joonistame läbi pöörlemistelje kehaga muutumatult ühendatud ja koos sellega pöörleva fikseeritud tasapinna I ja liikuva tasandi II (joonis 57). II tasapinna ja vastavalt ka kogu keha asend I tasapinna suhtes ruumis on täielikult määratud nurgaga 
. Kui keha pöörleb ümber telje 
see nurk on aja pidev ja üheväärtuslik funktsioon. Seetõttu, teades selle nurga muutumise seadust ajas, saame määrata keha asukoha ruumis:
-
keha pöörlemise seadus.
(43)
Sel juhul eeldame, et nurk 
fikseeritud tasapinnast telje positiivsest otsast vaadatuna vastupäeva 
. Kuna ümber fikseeritud telje pöörleva keha asendi määrab üks parameeter, siis öeldakse, et sellisel kehal on üks vabadusaste.
Nurkkiirus
Keha pöördenurga muutumist ajas nimetatakse nurgeliseks keha kiirus
ja tähistatud 
(oomega):
.(44)
Nurkkiirus, nagu ka lineaarkiirus, on vektorkogus ja see vektor 
ehitatud kere pöörlemisteljele. See on suunatud piki pöörlemistelge selles suunas, nii et selle otsast alguseni vaadates on näha keha pöörlemist vastupäeva (joon. 58). Selle vektori moodul määratakse sõltuvusega (44). Rakenduspunkt 
teljel saab suvaliselt valida, kuna vektorit saab tõlkida mööda selle tegevusjoont. Kui tähistame läbiva pöörlemistelje ortovektorit 
, siis saame nurkkiiruse vektoravaldise:
.
(45)
Nurkkiirendus
Keha nurkkiiruse muutumise kiirust ajas nimetatakse nurkkiirendus
kehad ja on tähistatud 
(epsilon):
.
(46)
Nurkkiirendus on vektori suurus ja see vektor 
ehitatud kere pöörlemisteljele. See on suunatud piki pöörlemistelge selles suunas, nii et selle otsast alguseni vaadates on näha epsiloni pöörlemissuunda vastupäeva (joon. 58). Selle vektori moodul määratakse sõltuvusega (46). Rakenduspunkt 
teljel saab suvaliselt valida, kuna vektorit saab tõlkida mööda selle tegevusjoont.
Kui tähistame läbiva pöörlemistelje ortovektorit 
, siis saame nurkkiirenduse vektoravaldise:
.
(47)
Kui nurkkiirus ja kiirendus on sama märgiga, siis keha pöörleb kiirendatud ja kui erinev - aeglaselt. Aeglase pöörlemise näide on näidatud joonisel fig. 58.
Mõelge pöörleva liikumise erijuhtudele.
1. Ühtlane pöörlemine: 
,
.
,
,
,
,
.
(48)
2. Võrdse muutujaga pöörlemine: 
.
,
,
,
,
,
,
,
,
,
,
.(49)
Lineaar- ja nurkparameetrite seos
Mõelge suvalise punkti liikumisele 
pöörlev keha. Sel juhul on punkti trajektoor ring, raadius 
, mis asub pöörlemisteljega risti olevas tasapinnas (joon. 59, aga).
Oletame, et tol ajal 
punkt on paigas 
. Oletame, et keha pöörleb positiivses suunas, s.o. nurga suurenemise suunas 
. Ajahetkel 
punkt võtab positsiooni 
. Tähistage kaar 
. Seetõttu teatud aja jooksul 
punkt on möödas 
. Tema keskmine kiirus
, ja millal 
,
. Kuid jooniselt fig. 59, b, see on selge 
. Siis. Lõpuks saame
.
(50)
Siin 
- punkti lineaarne kiirus 
. Nagu varem saadi, on see kiirus antud punktis suunatud trajektoorile tangentsiaalselt, st. puutuja ringiga.
Seega on pöörleva keha punkti lineaarse (ümbermõõdu) kiiruse moodul võrdne nurkkiiruse absoluutväärtuse korrutisega kaugusega sellest punktist pöörlemisteljeni.
Nüüd ühendame punkti kiirenduse lineaarsed komponendid nurga parameetritega.
,
.
(51)
Ümber fikseeritud telje pöörleva jäiga keha punkti tangentsiaalse kiirenduse moodul on võrdne keha nurkkiirenduse korrutisega sellest punktist pöörlemisteljeni.
,
.
(52)
Ümber fikseeritud telje pöörleva jäiga keha punkti normaalkiirenduse moodul on võrdne keha nurkkiiruse ruudu ja sellest punktist pöörlemistelje vahelise kauguse korrutisega.
Seejärel võtab punkti kogukiirenduse avaldis kuju
.
(53)
Vektorjuhised 
,
,
näidatud joonisel 59, sisse.
tasane liikumine Jäik keha on selline liikumine, mille käigus kõik keha punktid liiguvad paralleelselt mingi fikseeritud tasapinnaga. Sellise liikumise näited:
Iga keha liikumine, mille põhi libiseb mööda etteantud fikseeritud tasapinda;
Ratas veereb mööda sirget rööbastee lõiku.
Saame tasapinnalise liikumise võrrandid. Selleks arvestage lehe tasapinnas liikuvat lamedat kujundit (joonis 60). Viitame selle liikumise fikseeritud koordinaatsüsteemile 
, ja joonise endaga seostame liikuva koordinaatide süsteemi 
, mis liigub sellega kaasa.
Ilmselgelt määrab liikuva kujundi asukoha fikseeritud tasapinnal liikuvate telgede asend 
fikseeritud telgede suhtes 
. Selle asukoha määrab liikuva algpunkti asukoht 
, st. koordinaadid 
,
ja pöördenurk 
, liikuv koordinaatsüsteem fikseeritud koordinaadi suhtes, mida loendatakse teljest 
vastupäeva.
Järelikult määratakse tasapinnalise kujundi liikumine oma tasapinnas täielikult kindlaks, kui väärtused on teada iga ajahetke kohta 
,
,
, st. vormi võrrandid:
,
,
.
(54)
Võrrandid (54) on jäiga keha tasapinnalise liikumise võrrandid, kuna kui need funktsioonid on teada, siis iga ajahetke kohta on võimalik nendest võrranditest leida vastavalt 
,
,
, st. määrata liikuva kujundi asukoht antud ajahetkel.
Mõelge erijuhtudele:
1.
, siis on keha liikumine translatiivne, kuna liigutatavad teljed liiguvad, jäädes paralleelseks oma algpositsiooniga.
2.
,
. Selle liigutusega muutub ainult pöördenurk. 
, st. keha pöörleb ümber punkti läbiva kujundi tasapinnaga risti kulgeva telje 
.
Lameda kujundi liikumise lagunemine translatsiooniliseks ja pöörlevaks
Mõelge kahele järjestikusele positsioonile 
Ja 
kohati keha hõivatud 
Ja 
(joonis 61). keha asendist väljas 
asendisse 
saab üle kanda järgmiselt. Kõigepealt liigutame keha järk-järgult. Samal ajal segment 
liigub endaga paralleelselt asendisse 
, ja siis keerame keha ümber punkti (pooluse) 
nurga peal 
kuni punktide kokkulangevuseni 
Ja 
.
Järelikult mis tahes tasapinnalist liikumist saab esitada translatsioonilise liikumise summana koos valitud pooluse ja pöörleva liikumisega, selle pooluse kohta.
Vaatleme meetodeid, mille abil on võimalik määrata tasapinnalist liikumist tegeva keha punktide kiirusi.
1. Pooluse meetod. See meetod põhineb tasapinnalise liikumise jaotamisel translatsiooniliseks ja pöörlevaks. Lameda kujundi mis tahes punkti kiirust saab esitada kahe komponendina: translatsiooniline, kiirusega, mis on võrdne suvaliselt valitud punkti kiirusega -poolused , ja pöörlemine ümber selle pooluse.
Mõelge tasasele kehale (joonis 62). Liikumisvõrrandid on järgmised: 
,
,
.
Nende võrrandite põhjal määrame punkti kiiruse 
(nagu koordinaatide seadistusmeetodi puhul)
,
,
.
Seega punkti kiirus 
- väärtus on teada. Võtame selle punkti poolusena ja määrame suvalise punkti kiiruse 
keha.
Kiirus 
koosneb translatsioonikomponendist 
, punktiga kaasa liikudes 
ja pöörlev 
, kui punkt on pööratud 
punkti suhtes 
. Punkti kiirus 
liikuda punkti 
paralleelselt iseendaga, kuna translatsioonilises liikumises on kõikide punktide kiirused võrdsed nii suuruselt kui ka suunalt. Kiirus 
määratud sõltuvusega (50) 
, ja see vektor on suunatud raadiusega risti 
pöörlemissuunas 
. Vektor 
suunatakse mööda vektoritele ehitatud rööpküliku diagonaali 
Ja 
, ja selle mooduli määrab sõltuvus:
,
.(55)
2. Keha kahe punkti kiiruste projektsioonide teoreem.
Jäiga keha kahe punkti kiiruste projektsioonid neid punkte ühendaval sirgel on üksteisega võrdsed.
Mõelge keha kahele punktile 
Ja 
(joonis 63). Punkti võtmine 
pooluse kohta määrake suund 
sõltuvuse järgi (55): 
. Projekteerime selle vektori võrdsuse joonele 
ja seda arvestades 
risti 
, saame
3. Kiiruste hetkekeskpunkt.
Vahetu kiiruste keskpunkt(MCS) on punkt, mille kiirus antud ajahetkel on null.
Näitame, et kui keha ei liigu edasi, siis on selline punkt igal ajahetkel olemas ja pealegi ainulaadne. Las hetkel 
punktid 
Ja 
sektsioonis lebavad surnukehad 
, on kiirused 
Ja 
, ei ole üksteisega paralleelsed (joonis 64). Siis punkt 
, mis asub vektorite ristide ristumiskohas 
Ja 
, ja seal on MCS, alates 
.
Tõepoolest, kui me seda eeldame 
, siis teoreemi (56) järgi vektor 
peab olema risti 
Ja 
, mis on võimatu. Samast teoreemist on näha, et ükski teine lõik ei osuta 
sel ajahetkel ei saa kiirus olla nulliga võrdne.
Pooluse meetodi rakendamine 
- poolus, määrake punkti kiirus 
(55): alates 
,
. (57)
Sarnase tulemuse võib saada ka mis tahes muu kehapunkti puhul. Seetõttu on keha mis tahes punkti kiirus võrdne selle pöörlemiskiirusega MCS-i suhtes:
,
,
, st. keha punktide kiirused on võrdelised nende kaugustega MCS-ist.
Lameda kujundi punktide kiiruste määramise kolmest vaadeldud meetodist on näha, et MCS on eelistatavam, kuna siin määratakse kiirus kohe nii absoluutväärtuses kui ka ühe komponendi suunas. Seda meetodit saab aga kasutada, kui me teame või suudame määrata MCS-i asukoha keha jaoks.
MCS-i asukoha määramine
1. Kui me teame keha antud asukoha jaoks keha kahe punkti kiiruste suunad, siis MCC on nende kiirusvektorite ristide lõikepunkt.
2. Keha kahe punkti kiirused on antiparalleelsed (joon. 65, aga). Sel juhul on risti kiiruste suhtes ühine, st. MCC asub kuskil sellel risti. MCC asukoha määramiseks on vaja ühendada kiirusvektorite otsad. Selle sirge ja risti lõikepunkt on soovitud MCS. Sel juhul asub MCS nende kahe punkti vahel.
3. Keha kahe punkti kiirused on paralleelsed, kuid mitte võrdsed (joon. 65, b). MDS-i saamise protseduur on sarnane lõikes 2 kirjeldatule.
d) Kahe punkti kiirused on võrdsed nii suuruselt kui ka suunalt (joon. 65, sisse). Saame hetkelise translatsioonilise liikumise juhtumi, mille korral kõigi keha punktide kiirused on võrdsed. Seetõttu on keha nurkkiirus selles asendis null:
4. Määratleme fikseeritud pinnal libisemata veereva ratta MCC (joonis 65, joon. G). Kuna liikumine toimub libisemata, on ratta kokkupuutepunktis pinnaga kiirus sama ja võrdne nulliga, kuna pind on paigal. Seetõttu on ratta kokkupuutepunkt fikseeritud pinnaga MCC.
Tasapinnalise kujundi punktide kiirenduste määramine
Tasakujulise kujundi punktide kiirenduste määramisel saab jälgida analoogiat kiiruste määramise meetoditega.
1. Pooluse meetod. Nii nagu kiiruste määramisel, võtame pooluseks keha suvalise punkti, mille kiirendust me teame või saame määrata. Siis tasapinnalise kujundi mis tahes punkti kiirendus on võrdne pooluse kiirenduste ja selle pooluse ümber pöörleva liikumise kiirenduse summaga:
Samal ajal komponent 
määrab punkti kiirenduse 
kui see pöörleb ümber masti 
. Pööramisel on punkti trajektoor kõverjooneline, mis tähendab 
(joonis 66).
Siis võtab sõltuvus (58) kuju 
.
(59)
Võttes arvesse sõltuvusi (51) ja (52), saame 
,
.
2. Hetkeline kiirenduskese.
Vahetu kiirenduskeskus(MCC) on punkt, mille kiirendus antud ajahetkel on null.
Näitame, et selline punkt eksisteerib igal ajahetkel. Punkti võtame poolusena 
, mille kiirendus 
me teame. Nurga leidmine 
, lebab sees 
, ja tingimust rahuldav 
. Kui 
, siis 
ja vastupidi, st. süstimine 
on ladestunud suunas 
. Pange punktist kõrvale 
nurga all 
vektori juurde 
osa 
(joonis 67). Selliste konstruktsioonidega saadud punkt 
saab olema MCU.
Tõepoolest, punkti kiirendus 
võrdne kiirenduste summaga 
poolused 
ja kiirendus 
pöörlemisel ümber pooluse 
:
.
,
. Siis 
. Teisest küljest kiirendus 
moodustab segmendi suunaga 
süstimine 
, mis vastab tingimusele 
. Miinusmärk asetatakse nurga puutuja ette 
, alates pöörlemisest 
pooluse suhtes 
vastupäeva ja nurk 
ladestatakse päripäeva. Siis 
.
Järelikult 
ja siis 
.
MCC määramise erijuhud
1.
. Siis 
, ja seetõttu pole MCU-d olemas. Sel juhul liigub keha ette, st. keha kõikide punktide kiirused ja kiirendused on võrdsed.
2.
. Siis 
,
. See tähendab, et MCU asub keha punktide kiirenduste tegevusjoonte ristumiskohas (joonis 68, aga).
3.
. Siis 
,
. See tähendab, et MCC asub keha punktide kiirenduste ristide ristumiskohas (joonis 68, b).
4.
. Siis 
,
. See tähendab, et MCU asub keha nurga all olevate punktide kiirendustele tõmmatud kiirte ristumiskohas. 
(joon.68, sisse).
Vaatletud erijuhtudest võime järeldada: kui võtame punkti 
pooluse kohta, siis määratakse tasapinnalise kujundi mis tahes punkti kiirendus pöörleva liikumise kiirendusega ümber MCC:
.
(60)
Keeruline punkti liikumine nimetatakse sellist liikumist, milles punkt osaleb samaaegselt kahes või enamas liikumises. Sellise liikumise korral määratakse punkti asukoht mobiilseadme ja fikseeritud tugisüsteemide suhtes.
Punkti liikumist liikuva tugiraami suhtes nimetatakse punkti suhteline liikumine
. Tähistame suhtelise liikumise parameetreid 
.
Nimetatakse selle liikuva tugiraami selle punkti liikumist, millega liikuv punkt langeb antud hetkel kokku fikseeritud tugiraami suhtes. punkti liikumine
. Tähistagem kaasaskantava liikumise parameetreid 
.
Punkti liikumist fikseeritud tugiraami suhtes nimetatakse absoluutne (kompleksne)
punkti liikumine
. Tähistame absoluutse liikumise parameetreid 
.
Kompleksliikumise näitena võime vaadelda inimese liikumist liikuvas sõidukis (trammis). Sel juhul on inimese liikumine seotud liikuva koordinaatsüsteemiga - tramm ja fikseeritud koordinaatsüsteemiga - maa (tee). Siis on ülaltoodud definitsioonide põhjal inimese liikumine trammi suhtes suhteline, trammiga koos maapinna suhtes liikumine kujundlik ja inimese liikumine maapinna suhtes absoluutne.
Määrame punkti asukoha 
raadiused - vektorid liikuva suhtes 
ja liikumatult 
koordinaatsüsteemid (joon. 69). Tutvustame tähistust: 
- raadiuse vektor, mis määrab punkti asukoha 
liikuva koordinaatsüsteemi suhtes 
,
;
- raadiuse vektor, mis määrab liikuva koordinaatsüsteemi alguspunkti asukoha (punktid 
) (punktid 
);
- raadius - vektor, mis määrab punkti asukoha 
fikseeritud koordinaatsüsteemi suhtes 
;
,.
Saame suhtelistele, kujundlikele ja absoluutsetele liikumistele vastavad tingimused (piirangud).
1. Arvestades suhtelist liikumist, eeldame, et punkt 
liigub liikuva koordinaatsüsteemi suhtes 
ja liikuv koordinaatsüsteem ise 
fikseeritud koordinaatsüsteemi suhtes 
ei liigu.
Seejärel punkti koordinaadid 
muutub suhtelises liikumises ja liikuva koordinaatsüsteemi ortovektorid ei muutu suunas:
,
,
.
2. Arvestades teisaldatavat liikumist, eeldame, et punkti koordinaadid 
liikuva koordinaatsüsteemi suhtes on fikseeritud ja punkt liigub koos liikuva koordinaatsüsteemiga 
suhteliselt liikumatu 
:
,
,
,.
3. Absoluutsel liikumisel liigub punkt ka suhteliselt 
ja koos koordinaatsüsteemiga 
suhteliselt liikumatu 
:
Siis on kiiruste avaldised, võttes arvesse (27), kuju
,
,
Nende sõltuvuste võrdlemisel saame absoluutkiiruse avaldise: 
.
(61)
Saime teoreemi punkti kiiruste liitmise kohta keerulises liikumises: punkti absoluutne kiirus on võrdne kiiruse suhteliste ja teisaldatavate komponentide geomeetrilise summaga.
Kasutades sõltuvust (31), saame kiirenduste avaldised:
,
Nende sõltuvuste võrdlemisel saame absoluutse kiirenduse avaldise: 
.
Leiti, et punkti absoluutne kiirendus ei ole võrdne kiirenduste suhteliste ja teisaldatavate komponentide geomeetrilise summaga. Määratleme erijuhtude jaoks sulgudes oleva absoluutse kiirenduse komponendi.
1. Punkti translatiivne liikumine 
. Sel juhul liikuva koordinaatsüsteemi teljed 
liikuda kogu aeg paralleelselt iseendaga, siis. 
,
,
,
,
,
, siis 
. Lõpuks saame
.
(62)
Kui punkti teisaldatav liikumine on translatsiooniline, siis on punkti absoluutne kiirendus võrdne kiirenduse suhtelise ja teisaldatava komponendi geomeetrilise summaga.
2. Punkti kaasaskantav liikumine on mittetranslatiivne. Niisiis, antud juhul liikuv koordinaatsüsteem 
pöörleb nurkkiirusega ümber hetkelise pöörlemistelje 
(joonis 70). Tähistage vektori lõpus olevat punkti 
üle 
. Seejärel saame (15) täpsustamise vektormeetodit kasutades selle punkti kiirusvektori 
.
Teiselt poolt, 
. Võrdsustades nende vektorvõrduste õiged osad, saame: 
. Sarnaselt toimides saame ülejäänud vektorvektorite jaoks: 
,
.
Üldjuhul on punkti absoluutne kiirendus võrdne kiirenduse suhteliste ja kaasaskantavate komponentide geomeetrilise summaga pluss kaasaskantava liikumise nurkkiiruse vektori vektorkorrutis kahekordne vektori lineaarkiiruse vektor. suhteline liikumine.
Portatiivse liikumise nurkkiiruse vektori ja suhtelise liikumise lineaarkiiruse vektori kahekordistatud vektorkorrutist nimetatakse Coriolise kiirendus ja tähistatud
.
(64)
Coriolise kiirendus iseloomustab portatiivse liikumise suhtelise kiiruse muutust ja muutust kaasaskantav kiirus suhtelises liikumises.
Edastatud 
vektorkorrutise reegli järgi. Coriolise kiirendusvektor on alati suunatud vektorite moodustatud tasapinnaga risti 
Ja 
, nii et vektori lõpust vaadates 
, vaata pööret 
juurde 
, läbi väikseima nurga, vastupäeva.
Coriolise kiirendusmoodul on võrdne.
Jäiga keha pöörlev liikumine ümber fikseeritud telje on selline liikumine, mille korral mis tahes kaks kehale kuuluvat (või sellega alati seotud punkti) jäävad kogu liikumise vältel liikumatuks.(Joonis 2.2) .
Joonis 2.2
fikseeritud punktide läbimine AGA Ja IN sirgjoont nimetatakse pöörlemistelg. Kuna jäiga keha punktide vaheline kaugus peab jääma muutumatuks, on ilmne, et pöörleva liikumise ajal fikseeritakse kõik teljele kuuluvad punktid ja kõik ülejäänud kirjeldavad ringe, mille tasandid on risti pöörlemisteljega ja keskused asuvad sellel teljel. Pöörleva keha asukoha määramiseks joonistame läbi pöörlemistelje, mida mööda telg on suunatud Az, pool lennuk І - fikseeritud ja pooltasapinnaline ІІ põimitud kehasse endasse ja pöörleb koos sellega. Siis määrab keha asendi igal ajahetkel üheselt vastava märgiga võetud nurga järgi φ nende tasandite vahel, mida me nimetame keha nurk. Me kaalume nurka φ positiivne, kui see hilineb fikseeritud tasapinnalt vastupäeva (telje positiivsest otsast vaadates vaatleja jaoks Az), kuid päripäeva negatiivselt. mõõta nurka φ on radiaanides. Et teada saada keha asendit igal ajal, peate teadma nurga sõltuvust φ ajast t, st.
|
|
.See võrrand väljendab jäiga keha pöörlemise seadus ümber fikseeritud telje.
Jäiga keha pöörleva liikumise peamised kinemaatilised omadused on selle nurkkiirus ω ja nurkkiirendus ε.
9.2.1. Keha nurkkiirus ja nurkiirendus
Pöörlemisnurga φ muutumise kiirust ajas iseloomustavat väärtust nimetatakse nurkkiiruseks.
Kui teatud aja jooksul 
keha teeb pöörde 
, siis on keha arvuliselt keskmine nurkkiirus sellel ajavahemikul 
. Limiidis kl 
saame
Sellel viisil, keha nurkkiiruse arvväärtus antud ajahetkel on võrdne pöördenurga esimese tuletisega aja suhtes.
Märkide reegel: kui pöörlemine on vastupäeva, ω> 0 ja kui päripäeva, siis ω< 0.
või kuna radiaan on mõõtmeteta suurus, 
.
Teoreetilistes arvutustes on mugavam kasutada nurkkiiruse vektorit 
, mille moodul on võrdne 
ja mis on suunatud piki keha pöörlemistelge suunas, kust pöörlemine on nähtav vastupäeva. See vektor määrab koheselt nurkkiiruse mooduli ja pöörlemistelje ning pöörlemissuuna ümber selle telje.
Suurust, mis iseloomustab nurkkiiruse muutumise kiirust ajas, nimetatakse keha nurkkiirenduseks.
Kui teatud aja jooksul 
nurkkiiruse juurdekasv on võrdne 
, siis suhe 
, st. määrab pöörleva keha keskmise kiirenduse väärtuse ajas 
.
Kui pingutada 
saame hetkel nurkkiirenduse väärtuse t:
Sellel viisil, keha nurkkiirenduse arvväärtus antud ajahetkel on võrdne keha nurkkiiruse esimese tuletise või teise pöördenurga tuletisega ajas.
Mõõtühik on tavaliselt 
või, mis on samuti 
.
Kui nurkkiiruse moodul aja jooksul suureneb, nimetatakse keha pöörlemist kiirendatud ja kui see väheneb, - aeglane. Kui kogused ω
Ja ε
on samad märgid, siis pöörlemine kiireneb, kui erinev - aeglustunud. 
Analoogiliselt nurkkiirusega saab nurkiirendust esitada ka vektorina 
suunatud piki pöörlemistelge. Kus
.
Kui keha pöörleb kiirendatud suunaga 
langeb kokku 
, ja vastupidi 
aeglase pöörlemise ajal.
Kui keha nurkkiirus jääb liikumise ajal konstantseks ( ω= konst), siis nimetatakse keha pöörlemist ühtlane.
Alates 
meil on 
. Seega, eeldades, et esialgsel ajahetkel 
süstimine 
ja integraalide võtmine vasakule 
enne 
ja paremal 0 kuni t, lõpuks saame
|
|
.Ühtlase pöörlemisega, millal 
=0,
Ja 
.
Ühtlase pöörlemiskiiruse määrab sageli pöörete arv minutis, tähistades seda väärtust kui n p/min Leiame omavahelised suhted n rpm ja ω 1/s. Ühe pöördega pöörleb keha 2π võrra ja koos n pööret 2π kohta n; see pööre tehakse 1 min, st. t= 1 min = 60 s. Sellest järeldub
|
|
.Kui keha nurkkiirendus jääb kogu liikumise vältel konstantseks (ε = konst), siis nimetatakse pöörlemist võrdselt muutlikud.
Algsel ajahetkel t=0 nurk 
ja nurkkiirus 
(
- algnurkkiirus). 
;
=ε 
. Vasaku külje integreerimine 
enne 
ja parempoolne 0 kuni t, leia
Selle pöörlemise nurkkiirus ω 
. Kui ω ja ε märgid on samad, on pöörlemine ühtlaselt kiirendatud, ja kui erinev sama aeglane.
Jäiga keha pöörlev liikumine. Pöörlemine on jäiga keha liikumine, mille käigus kõik selle punktid, mis asuvad kindlal sirgel, mida nimetatakse pöörlemisteljeks, jäävad liikumatuks.
Pöörleva liikumise ajal liiguvad kõik ülejäänud keha punktid pöörlemisteljega risti olevatel tasapindadel ja kirjeldavad ringe, mille keskpunktid asuvad sellel teljel.
Pöörleva keha asukoha määramiseks joonistame läbi z-telje kaks pooltasapinda: pooltasand I - fikseeritud ja pooltasand II - ühendatud tahke kehaga ja sellega pöörlev (joon. 2.4). Siis määrab keha asend igal ajahetkel üheselt nurga järgi j nende pooltasandite vahel, mis on võetud vastava märgiga, mida nimetatakse keha pöördenurgaks.
Kui keha pöörleb, muutub pöördenurk j sõltuvalt ajast, st see on aja t funktsioon:
Seda võrrandit nimetatakse võrrand jäiga keha pöörlev liikumine.
Jäiga keha pöörleva liikumise peamised kinemaatilised karakteristikud on selle nurkkiirus w ja nurkiirendus e.
Kui õigel ajal D t= t1 + t keha teeb pöörde võrra Dj = j1 –j, siis on keha keskmine nurkkiirus sellel ajavahemikul võrdne
(1.16)
Keha nurkkiiruse väärtuse määramiseks antud ajahetkel t leida pöördenurga juurdekasvu Dj ja ajavahemiku D suhte piir t kuna viimane kipub nulli:
(2.17)
Seega on keha nurkkiirus antud ajahetkel arvuliselt võrdne pöördenurga esimese tuletisega aja suhtes. Nurkkiiruse w märk langeb kokku keha pöördenurga märgiga j: w > 0 j jaoks > 0 ja vastupidi, kui j < 0. siis w < 0. Nurkkiiruse ühik on tavaliselt 1/s, seega on radiaan dimensioonitu suurus.
Nurkkiirust saab esitada vektorina w , mille arvväärtus on võrdne dj/dt-ga, mis on suunatud piki keha pöörlemistelge suunas, kust nähakse pöörlemist vastupäeva.
Keha nurkkiiruse muutumine ajas iseloomustab nurkkiirendust e. Analoogiliselt nurkkiiruse keskmise väärtuse leidmisega leiame avaldise keskmise kiirenduse väärtuse määramiseks:
(2.18)
Seejärel määratakse avaldise järgi jäiga keha kiirendus antud ajahetkel
(2.19)
st keha nurkiirendus antud ajahetkel on võrdne keha nurkkiiruse esimese tuletise või keha pöördenurga teise tuletisega aja suhtes. Nurkkiirenduse mõõde on 1/s 2 .
Jäiga keha nurkiirendust, nagu ka nurkkiirust, saab esitada vektorina. Nurkkiirenduse vektor langeb tahke ülaosa kiirendatud liikumise ajal kokku nurkkiiruse vektoriga ja aegluubis on suunatud vastupidises suunas.
Olles kindlaks teinud jäiga keha kui terviku liikumise tunnused, jätkakem selle üksikute punktide liikumise uurimisega. Mõelge mõnele punktile M jäik keha, mis asub pöördeteljest r kaugusel h (joonis 2.3).
Kui keha pöörleb, kirjeldab punkt M ümbermõõtu raadiusega h, mis on tsentreeritud pöörlemisteljel ja asub selle teljega risti. Kui aja dt jooksul toimub keha elementaarne pööre nurga dj all , siis punkt M samal ajal teostab see elementaarse nihke piki oma trajektoori dS = h * dj ,. Seejärel määrati avaldise järgi punkti M kiirus
(2.20)
Kiirust nimetatakse punkti M lineaar- ehk ringkiiruseks.
Seega on pöörleva jäiga keha punkti joonkiirus arvuliselt võrdne keha nurkkiiruse ja kauguse korrutisega sellest punktist pöörlemisteljeni. Kuna keha kõigi punktide nurkkiirus w; on sama väärtusega, siis joonkiiruse valemist järeldub, et pöörleva keha punktide joonkiirused on võrdelised nende kaugustega pöörlemisteljest. Jäiga keha punkti lineaarkiirus on vektor n, mis on suunatud punktiga kirjeldatud ringjoonele tangentsiaalselt M.
Valge on kaugus tahke tuha pöörlemisteljelt teatud punktini M vaadeldakse punkti M raadiusvektoriks h, siis punkti v lineaarkiiruse vektorit saab esitada nurkkiiruse vektori korrutisena w raadiuse vektor h:
V = w * h (2/21)
Tõepoolest, vektorkorrutise (2.21) tulemus on vektor, mis on absoluutväärtuselt võrdne korrutisega w * h ja mis on suunatud (joonis 2.5) risti tasapinnaga, millel kaks tegurit asuvad, suunas, millest lähim kombinatsioon Esimese teguri puhul täheldatakse teise teguri esinemist vastupäeva, st punkti M trajektoori puutuja suhtes.
Seega ristkorrutisest (2.21) tulenev vektor vastab absoluutväärtuselt ja suunalt punkti M lineaarkiiruse vektorile.
Riis. 2.5
Kiirenduse väljenduse leidmiseks aga punkt M teostame avaldise (2.21) ajalise diferentseerimise punkti kiiruse jaoks
(2.22)
Arvestades, et dj/dt=e ja dh/dt = v, kirjutame avaldise (2.22) järgmiselt
kus a r ja an on vastavalt keha punkti kogukiirenduse tangentsiaalne ja normaalkomponent pöörleva liikumise ajal, mis määratakse avaldiste põhjal
Kehapunkti täiskiirenduse tangentsiaalne komponent (tangentsiaalne kiirendus) at iseloomustab kiirusvektori mooduli muutumist ja on suunatud tangentsiaalselt kehapunkti trajektoorile kiirendatud liikumisel kiirusvektori suunas või vastupidises suunas. aegluubi ajal. Keha punkti tangentsiaalse kiirenduse vektori moodul jäiga keha pöörlemise ajal määratakse avaldisega
(2,25)
Täiskiirenduse tavaline komponent (tavaline kiirendus) aga" tekib tahke keha värvimisel punkti kiirusvektori suuna muutumise tõttu. Nagu tavakiirenduse avaldisest (2.24) järeldub, on see kiirendus suunatud piki raadiust h ringi keskpunkti, mida mööda punkt liigub. Punkti normaalkiirenduse vektori moodul jäiga keha pöörlemise ajal määratakse, võttes arvesse (2.20), avaldisega
