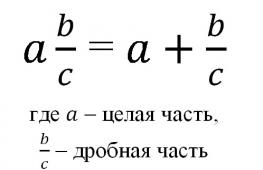Важным параметром решения систем уравнений является. Решение уравнений с параметром по математике

05.04.2020

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а 2 – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:

1/1 = (а 2 – 3)/1 ≠ а/2 или систему

{а 2 – 3 = 1,
{а ≠ 2.

Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ . Решаем методом подстановки.

{2 – у + (а 2 – 3)у = а,
{х = 2 – у,

{(а 2 – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а 2 – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а 2 – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х 2 = 1.

Решение.

Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:

1,25 = 0,5 + а;

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;

а 2 х + 3ах = 2 + а 2 + 3а + 2.

Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а 2 + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,

а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х 2 + у 2 = 9,
{у – |х| = а.

Решение.

Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.

Ответ: а = 3.

Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Уравнение вида f (x ; a ) = 0 называется уравнением с переменной х и параметром а .

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х , удовлетворяющие этому уравнению.

Пример 1. ах = 0

Пример 2. ах = а

Пример 3.

х + 2 = ах
х – ах = -2
х(1 – а) = -2

Если 1 – а = 0, т.е. а = 1, то х 0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

(а 2 – 1) х = 2а 2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х .

Например:

если а = 5, то х = = ;

если а = 0, то х = 3 и т. д.

Дидактический материал

1. ах = х + 3

2. 4 + ах = 3х – 1

3. а = +

при а = 1 корней нет.

при а = 3 корней нет.

при а = 1 х – любое действительное число, кроме х = 1

при а = -1, а = 0 решений нет.

при а = 0, а = 2 решений нет.

при а = -3, а = 0, 5, а = -2 решений нет

при а = -с , с = 0 решений нет.

Квадратные уравнения с параметром

Пример 1. Решить уравнение

(а – 1)х 2 = 2(2а + 1)х + 4а + 3 = 0

При а = 1 6х + 7 = 0

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

20а + 16 = 0

20а = -16

Если а < -4/5, то Д < 0, уравнение имеет действительный корень.

Если а > -4/5 и а 1, то Д > 0,

х =

Если а = 4/5, то Д = 0,

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

Д = 4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28а + 24 = 4(а – 1)(а – 6)

4(а – 1)(а – 6) > 0

по т. Виета: х 1 + х 2 = -2(а + 1)
х 1 х 2 = 9а – 5

По условию х 1 < 0, х 2 < 0 то –2(а + 1) < 0 и 9а – 5 > 0

В итоге

4(а – 1)(а – 6) > 0
- 2(а + 1) < 0
9а – 5 > 0

а < 1: а > 6
а > - 1
а > 5/9

(Рис. 1 )

< a < 1, либо a > 6

Пример 3. Найдите значения а , при которых данное уравнение имеет решение.

х 2 – 2(а – 1)х + 2а + 1 = 0

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а (а – 4) 0

а(а – 4)) 0

а(а – 4) = 0

а = 0 или а – 4 = 0
а = 4

(Рис. 2 )

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

1. При а = - 1/7, а = 0, а = 1

2. При а = 0

3. При а = 2

4. При а = 10

5. При а = - 2

Показательные уравнения с параметром

Пример 1 .Найти все значения а , при которых уравнение

9 х – (а + 2)*3 х-1/х +2а *3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х, получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у , тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

(у – 2)(у – а ) = 0, откуда у 1 =2, у 2 = а .

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log 3 2 , или х 2 – х log 3 2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 3 2 – 4 < 0.

Если у = а , т.е. 3 х+1/х = а то х + 1/х = log 3 а , или х 2 – х log 3 а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 3 2 – 4 > 0, или |log 3 а| > 2.

Если log 3 а > 2, то а > 9, а если log 3 а < -2, то 0 < а < 1/9.

Ответ: 0 < а < 1/9, а > 9.

Пример 2 . При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х 1 = -3, х 2 = а = >

а – положительное число.

Ответ: при а > 0

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х - (5а -3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Логарифмические уравнения с параметром

Пример 1. Найти все значения а , при которых уравнение

log 4x (1 + ах ) = 1/2 (1)

имеет единственное решение.

Решение. Уравнение (1) равносильно уравнению

1 + ах = 2х при х > 0, х 1/4 (3)

х = у

ау 2 –у + 1 = 0 (4)

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.Чтобы решить неравенство (3), построим графики функций Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1990

Крамор В.С . Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 1990.

Галицкий М.Л., Гольдман А.М., Звавич Л.И . Сборник задач по алгебре. – М.: Просвещение, 1994.

Звавич Л.И., Шляпочник Л.Я. Алгебра и начала анализа. Решение экзаменационных задач. – М.: Дрофа, 1998.

Макарычев Ю.Н. и др. Дидактические материалы по алгебре 7, 8, 9 кл. – М.: Просвещение, 2001.

Саакян С.И., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа для 10–11-х классов. – М.: Просвещение, 1990.

Журналы “Математика в школе”.

Л.С. Лаппо и др. ЕГЭ. Учебное пособие. – М.: Экзамен, 2001–2008.

Цель:

повторить решение систем линейных уравнений с двумя переменными
дать определение системы линейных уравнений с параметрами
научит решать системы линейных уравнений с параметрами.

Ход урока

Организационный момент
Повторение
Объяснение новой темы
Закрепление
Итог урока
Домашнее задание

2. Повторение:

I. Линейное уравнение с одной переменной:

1. Дайте определение линейного уравнения с одной переменной

[Уравнение вида ax=b, где х – переменная, а и b некоторые числа, называется линейным уравнением с одной переменной]

2. Сколько корней может иметь линейное уравнение?

[- Если а=0, b0, то уравнение не имеет решений, х

Если а=0, b=0, то х R

Если а0, то уравнение имеет единственное решение, х =

3. Выясните, сколько корней имеет уравнение (по вариантам)

II. Линейное уравнение с 2 –мя переменными и система линейных уравнений с 2- мя переменными.

1. Дайте определение линейного уравнения с двумя переменными. Приведите пример.

[Линейным уравнением с двумя переменными называются уравнения вида ах +by=с, где х и у – переменные, а, b и с – некоторые числа. Например, х-у=5]

2. Что называется решением уравнения с двумя переменными?

[Решением уравнения с двумя переменными называются пара значений переменных, обращающие это уравнение в верное равенство.]

3. Является ли пара значений переменных х = 7, у = 3 решением уравнения 2х + у = 17?

4. Что называется графиком уравнения с двумя переменными?

[Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых является решениями этого уравнения.]

5. Выясните, что представляет собой график уравнения:

[Выразим переменную у через х: у=-1,5х+3

Формулой у=-1,5х+3 является линейная функция, графиком которой служит прямая. Так как, уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6]

6. Что является графиком уравнения ах+bу=с с переменными х и у, где а0 или b0?

[Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.]

7. Что называется решением системы уравнений с двумя переменными?

[Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство]

8. Что значит решить систему уравнений?

[Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.]

9. Выясните, всегда ли имеет такая система решения и если имеет, то сколько (графическим способом).

10. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

[Единственное решение, если прямые пересекаются; не имеет решений, если прямые параллельны; бесконечно много, если прямые совпадают]

11. Каким уравнением обычно задается прямая?

12. Установите связь между угловыми коэффициентами и свободными членами:

I вариант:

у=-х+2
y= -x-3,

k 1 = k 2 , b 1 b 2, нет решений;

II вариант:

y=-х+8
y=2x-1,

k 1 k 2 , одно решение;

III вариант:

y=-x-1
y=-x-1,

k 1 = k 2 , b 1 = b 2, много решений.

Вывод:

Если угловые коэффициенты прямых являющихся графиками этих функций различны, то эти прямые пересекаются и система имеет единственное решение.
Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые параллельны, а система не имеет решений.
Если угловые коэффициенты и точки пересечения с осью у одинаковы, то прямые совпадают и система имеет бесконечно много решений.

На доске таблица, которую постепенно заполняет учитель вместе с учениками.

III. Объяснение новой темы.

Определение: Система вида

A 1 x+B 1 y=C
A 2 x+B 2 y=C 2

где A 1, A 2, B 1 ,B 2, C 1 C 2 – выражения, зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

Возможны следующие случаи:

1) Если , то система имеет единственное решение

2) Если , то система не имеет решений

3) Если , то система имеет бесконечно много решений.

IV. Закрепление

Пример 1.

При каких значениях параметра а система

2х - 3у = 7
ах - 6у = 14

а) имеет бесконечное множество решений;

б) имеет единственное решение

Ответ:

а) если а=4, то система имеет бесконечное множество решений;

б) если а 4, то решение единственное.

Пример 2.

Решите систему уравнений

x+(m+1)y=1
x+2y=n

Решение: а) , т.е. при m1 система имеет единственное решение.

б) , т.е. при m=1 (2=m+1) и n1 исходная система решений не имеет

в) , при m=1 и n=1 система имеет бесконечно много решений.

Ответ: а) если m=1 и n1, то решений нет

б) m=1 и n=1, то решение бесконечное множество

у - любое
x=n-2y

в) если m1 и n - любое, то

Пример 3.

ах-3ау=2а+3
х+ау=1

Решение: Из II уравнения найдем х=1-ау и подставим в I уравнение

а(1-ау)-3ау=2а+3

а-а 2 у-3ау=2а+3

А 2 у-3ау=а+3

А(а+3)у=а+3

Возможны случаи:

1) а=0. Тогда уравнение имеет вид 0*у=3 [у ]

Следовательно, при а=0 система не имеет решений

2) а=-3. Тогда 0*у=0.

Следовательно, у . При этом х=1-ау=1+3у

3) а0 и а-3. Тогда у=-, х=1-а(-=1+1=2

Ответ:

1) если а=0, то (х; у)

2) если а=-3, то х=1+3у, у

3) если а 0 и а?-3, то х=2, у=-

Рассмотрим II способ решения системы (1).

Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В 2, второе на – В 1 и сложим почленно эти уравнения, исключив, таким образом, переменную у:

Т.к. А 1 В 2 -А 2 В 1 0, то х =

Теперь исключим переменную х. Для этого умножим первое уравнение системы (1) на А 2 , а второе на – А 1 , и оба уравнения сложим почленно:

А 1 А 2 х +А 2 В 1 у=А 2 С 1
-А 1 А 2 х-А 1 В 2 у=-А 1 С 2
у(А 2 В 1 -А 1 В 2)=А 2 С 1 -А 1 С 2

т.к. А 2 В 1 -А 1 В 2 0 у =

Для удобства решения системы (1) введем обозначения:

- главный определитель

Теперь решение системы (1) можно записать с помощью определителей:

Приведенные формулы называют формулами Крамера.

Если , то система (1) имеет единственное решение: х=; у=

Если , или , , то система (1) не имеет решений

Если , , , , то система (1) имеет бесконечное множество решений.

В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае часто бывает удобно исследовать систему следующим образом: решая уравнение , найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую надо и исследовать.

Если коэффициенты А 1 , А 2 , В 1 , В 2 , системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.

Пример 4.

Для всех значений параметра а решить систему уравнений

(а+5)х+(2а+3)у=3а+2
(3а+10)х+(5а+6)у=2а+4

Решение: Найдем определитель системы:

= (а+5)(5а+6) – (3а+10) (2а+3)= 5а 2 +31а+30-6а 2 -29а-30=-а 2 +2а=а(2-а)

= (3а+2) (5а+6) –(2а+4)(2а+3)=15а 2 +28а+12-4а 2 -14а-12=11а 2 +14а=а(11а+14)

=(а+5) (2а+4)-(3а+10)(3а+2)=2а 2 +14а+20-9а 2 -36а-20=-7а 2 -22а=-а(7а+22)

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В математике существуют задачи, в которых необходимо произвести поиск решений линейных и квадратных уравнений в общем виде или произвести поиск количества корней, которое имеет уравнение в зависимости от значения параметра. Все эти задачи с параметрами.

Рассмотрим следующие уравнения в качестве наглядного примера:

\[у = kx,\] где \ - переменные, \- параметр;

\[у = kx + b,\] где \ - переменные, \ - параметр;

\[аx^2 + bх + с = 0,\] где \ - переменная, \[а, b, с\] - параметр.

Решить уравнение с параметром значит, как правило, решить бесконечное множество уравнений.

Однако, придерживаясь определенного алгоритма, можно легко решить такие уравнения:

1. Определить "контрольные" значения параметра.

2. Решить исходное уравнение относительно [\x\] при значениях параметра, определенных в первом пункте.

3. Решить исходное уравнение относительно [\x\] при значениях параметра, отличающихся от выбранных в первом пункте.

Допустим, дано такое уравнение:

\[\mid 6 - x \mid = a.\]

Проанализировав исходные данные, видно, что a \[\ge 0.\]

По правилу модуля \ выразим \

Ответ: \ где \

Где можно решить уравнение с параметром онлайн?

Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать - это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

1. Системы линейных уравнений с параметром

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а 2 – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1/1 = (а 2 – 3)/1 ≠ а/2 или систему

{а 2 – 3 = 1,
{а ≠ 2.

Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ . Решаем методом подстановки.

{2 – у + (а 2 – 3)у = а,
{х = 2 – у,

{(а 2 – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а 2 – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а 2 – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х 2 = 1.

Решение.

1,25 = 0,5 + а;

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;

а 2 х + 3ах = 2 + а 2 + 3а + 2.

Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а 2 + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,

а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

{х 2 + у 2 = 9,
{у – |х| = а.

Решение.

Ответ: а = 3.

Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.