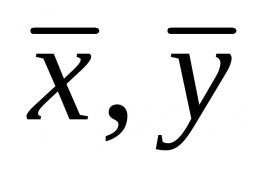Kaugus punktist punkti, valemid, näited, lahendused. Kuidas leida kaugust koordinaattasandil Kuidas leida kaugust koordinaatjoonel

Õppetund nr 3

TEEMA: Koordinaatjoone punktide vaheline kaugus

Õpetaja tegevuse eesmärk: luua tingimused koordinaatjoone punktide vahekauguse leidmise oskuse omandamiseks, erinevuse mooduli, lõigu keskkoha koordinaatide arvutamiseks.

Teema uurimise kavandatud tulemused:

Isiklik: ilmutada huvi aine õppimise vastu.

Teema: oskab leida koordinaatjoone punktide vahelist kaugust, arvutades erinevuse moodulit, lõigu keskkoha koordinaate.

Teema õppimise metaaine tulemused (universaalsed õppetegevused):

kognitiivne: keskenduda erinevatele probleemide lahendamise viisidele; oskab teavet kokku võtta ja süstematiseerida;

regulatiivne: arvestama reegliga lahendusmeetodi planeerimisel ja kontrollimisel;

suhtlemisaldis: arvestama erinevate arvamustega ja püüdma koostöös erinevaid seisukohti kooskõlastada.

Tunni skript.

I .org hetk.
Tere kutid. Täna oleme külas, tervitame neid!

Istu maha.

Meil pole tüüpilist klassi. Teadmiste üldistamise tund. Peame näitama, mida oleme õppinud, mida oleme õppinud.

Mis teemaga oleme viimasel ajal tegelenud? (võrdlus, ratsionaalsete arvude liitmine)

Tunni epigraafiks võtsin need sõnad : Me läheme täna teadusreisile

Võtame appi fantaasia

Me ei keera sirgelt teelt maha

Ja selleks, et jõuaksime oma eesmärkideni kiiremini

Peame trepist üles minema!

2. Teadmiste uuendamine .

Ülesanne "Redel".

Varianttöö, kontrollimine ja enesehindamine

3 Hästi tehtud, jätkame teadmiste poole liikumist.Kontrollime oma kodutööd.

1. Leidke koordinaatjoone punktide vaheline kaugus: D / Z

a) A(-4) ja B(-6); b) A(5) ja B(-7); c) A(3) ja B(-18).

LAHENDUS: a) AB = |-6-(-4) |= |-2|=2

b) AB =|-7-5|=12

c) AB = |-18-3 |= 21

2. Leidke punktist kaugemate punktide koordinaadid:

a) A(-8) 5 võrra; b) B(6) -2,7 võrra; c) C(4) kuni -3,2

Lahendus: a) -8+5=-3 AGA 1 (-3) ja -8-5=-13 AGA 2 (-13)

b) 6 + (-2,7) \u003d 3,3 AT 1 (3,3) ja 6-(-2,7)=8,7 AT 2 (8,7)

c) 4+(-3,2) = 0,8 FROM 1 (0,8) 4-(-3,2) = 7,2 FROM 2 (7,2)

3) Leidke punkti C koordinaat, lõigu keskpunkt, kui:

a) A(-12) B(1) b) A(-7) ja B(9) c) A(16) ja B (-8)

LAHENDUS:

12+1=-11 B) -7+9 =2 C) 16+(-8) =8

11: 2=-5,5 2:2=1 8:2 =4

С(-5,5) С(1) С(4)

Teie laual on kodutöö näidis. Kontrollige ja hinnake enesehinnangulehte.

4 . Blitz – küsitlus :

1. Mis on koordinaatjoon?

2. Milliseid ratsionaalarvude võrdlemise reegleid tead?

3. Mis on arvu moodul?

4. Kuidas liita kahte samade märkidega numbrit?

5. Kuidas liita kahte erineva märgiga numbrit?

6. Kuidas määrata koordinaatjoone punktide vahelist kaugust?

Noh, nüüd näitame, kuidas saame oma teadmisi praktikas rakendada.

5. Parandage vead

    12+4 =-16 -12+(-18) =6 9-14=5

    16 +(-10)=6 30 +(-10) =-20 5 –(-3)=2

    6 –(-5) =11 -20 -14 =-34 -2 +7=9

    11-28 =-39 -34 -5 =-29 9 -13=22

Tehke enesetest.

    12+4 =--8 -12+(-18) =30 9-14= -5

    16 +(-10)=-26 30 +(-10) =20 5 –(-3)=8

    26 –(-5) =-21 -20 -14 =-34 -2 +7=5

    11-28 =--17 -34 -5 =-41 9 -13=-4

6. Määrake punktide vaheline kaugus: ja leidke lõigu keskpunkt (vastavalt valikutele)

(märkmiku vahetus ja vastastikune kontroll.)



7. Noh, nüüd me puhkame. Meie silmad peavad puhkama

8. Iseseisva töö (vihikus) hindamine.

    1. variant 2. variant

    1,5-4,6 0,8 -1,2

    -2,8 +3,8 4-9,4

    0,45 -1 -4,3 +(-1,2) (9. slaid)

    Sihtmärk: kontrollida liitmise seaduste rakendamise oskust teisendusavaldiste puhul; arendada kognitiivset huvi, iseseisvust; kasvatada visadust ja sihikindlust eesmärgi saavutamisel.


    Leidke avaldise väärtus ja vastavalt tulemusele värvige päkapikk vastavalt tabelile. (kaart päkapikuga jääb õpilastele talismaniks)

    Hästi tehtud poisid!

    Sa täitsid ülesanded

    Ja säras teadmistest.

    Ja õppimise võluvõti -

    Teie visadust ja kannatlikkust!

Koordinaatjoone punktide vaheline kaugus - 6 klass.

Valem koordinaatjoone punktide vahelise kauguse leidmiseks

Algoritm punkti koordinaatide leidmiseks - lõigu keskpunkt

Aitäh kolleegidele Internetis, kelle materjali selles esitluses kasutasin!

Lae alla:

Eelvaade:

Esitluste eelvaate kasutamiseks looge Google'i konto (konto) ja logige sisse: https://accounts.google.com


Slaidide pealdised:

Koordinaatjoone punktide vaheline kaugus x 0 1 A B AB \u003d ρ (A, B)

Koordinaatsirge punktide vaheline kaugus Tunni eesmärk: - Leida viis (valem, reegel) koordinaatjoone punktide vahelise kauguse leidmiseks. - Õppige leidma leitud reegli abil koordinaatjoone punktide vahelist kaugust.

1. Suuline loendamine 15 -22 +8 -31 +43 -27 -14

2. Lahendage ülesanne suuliselt, kasutades koordinaatjoont: mitu täisarvu on arvude vahel: a) - 8,9 ja 2 b) - 10,4 ja - 3,7 c) - 1,2 ja 4,6? a) 10 b) 8 c) 6

0 1 2 7 positiivsed numbrid -1 -5 negatiivset numbrit Kaugus kodust staadionini 6 Kaugus kodust koolini 6 Koordinaatjoon

0 1 2 7 -1 -5 Kaugus staadionist koduni 6 Kaugus koolist koduni 6 Punktide vahelise kauguse leidmine koordinaatjoonel ρ (-5 ; 1)=6 ρ (7 ; 1)=6 Punktide vaheline kaugus tähistatakse tähega ρ (rho)

0 1 2 7 -1 -5 Kaugus staadionist koduni 6 Kaugus koolist koduni 6 Koordinaatjoone punktide vahelise kauguse leidmine ρ (-5 ; 1)=6 ρ (7 ; 1)=6 ρ (a; b) = ? | a-b |

Punktide a ja b vaheline kaugus on võrdne nende punktide koordinaatide erinevuse mooduliga. ρ (a; b)= | a-b | Koordinaatjoone punktide vaheline kaugus

Reaalarvu mooduli geomeetriline tähendus a b a a=b b x x x Kahe punkti vaheline kaugus

0 1 2 7 -1 -5 Leidke koordinaatjoone punktide vahelised kaugused - 2 - 3 - 4 3 4 5 6 -6 ρ (-6 ; 2)= ρ (6 ; 3)= ρ (0 ; 7) = ρ (1 ; -4) = 8 3 7 5

0 1 2 7 -1 -5 Leidke koordinaatjoone punktide vahelised kaugused - 2 - 3 - 4 3 4 5 6 -6 ρ (2 ; -6)= ρ (3 ; 6)= ρ (7 ; 0) = ρ (-4 ; 1) = 8 3 7 5

Väljund: avaldise väärtused| a-b | ja | b-a | on võrdsed a ja b = mis tahes väärtuste korral

–16 –2 0 –3 +8 0 +4 +17 0 ρ(–3; 8) = 11; |(–3) – (+8)| = 11; |(+8) – (–3)| = 11. ρ(–16; –2) = 14; |(–16) – (–2)| = 14; |(–2) – (–16)| = 14. ρ(4; 17) = 13; |(+4) – (+17)| = 13; |(+17) – (+4)| = 13. Koordinaatjoone punktide vaheline kaugus

Leidke ρ(x; y)kui: 1) x = -14, y = -23; ρ(x; y)=| x – y |=|–14–(– 23)|=|–14+23|=| 9 |=9 2) x = 5,9, y = -6,8; ρ(x; y)=|5, 9 –(– 6,8)|=|5,9+6,8|=| 12,7 |=12,7

Jätkake lauset 1. Koordinaatsirge on sirge ... 2. Kahe punkti vaheline kaugus on ... 3. Vastandarvud on arvud, ... 4. Arvu X moodulit nimetatakse ... 5 - Võrrelge avaldiste väärtusi - b V b - a järeldus … - Võrrelge avaldiste väärtusi | a-b | v | b-a | c järeldada...

Vintik ja Shpuntik kõnnivad mööda koordinaatkiirt. Kruvi on punktis B(236), Shpuntik punktis W(193) Kui kaugel on Kruvi ja Shpuntik üksteisest? ρ(B, W) = 43

Leidke punktide A (0), B (1) A (2), B (5) A (0), B (- 3) A (- 10), B (1) AB \u003d 1 AB \u003d vaheline kaugus 3 AB \u003d 3 AB = 11

Leidke punktide A (- 3,5), B (1,4) K (1,8), B (4,3) A (- 10), C (3) vaheline kaugus

Kontrollige AB = KV = AC =

C (- 5) C (- 3) Leidke punkti koordinaat - lõigu BA keskkoht

Koordinaatjoonele on märgitud punktid A (–3,25) ja B (2,65). Leidke punkti O koordinaat - lõigu AB keskpunkt. Lahendus: 1) ρ(А;В)= |–3,25 – 2,65| = |–5,9| \u003d 5,9 2) 5,9: 2 \u003d 2,95 3) -3,25 + 2,95 \u003d - 0,3 või 2,65 - 2,95 \u003d - 0,3 Vastus: O (-0, 3)

Koordinaatjoonele on märgitud punktid С(–5.17) ja D(2.33). Leidke punkti A koordinaat - lõigu CD keskpunkt. Lahendus: 1) ρ(С; D)= |– 5 , 17 – 2, 33 | = |– 7 , 5 | \u003d 7, 5 2) 7, 5: 2 \u003d 3, 7 5 3) - 5, 17 + 3, 7 5 \u003d - 1, 42 või 2, 33 - 3, 7 5 \u003d - 1, 4 Vastus: A ( - 1, 42)

Järeldus: Punkti koordinaadi leidmise algoritm - antud lõigu keskkoht: 1. Leidke punktide vaheline kaugus - antud lõigu otsad = 2. Jagage tulemus-1 2-ga (pool väärtusest) = c 3. Lisa tulemus-2 koordinaadile a või lahuta tulemus-2 koordinaadist a + c või - c 4. Tulemus-3 on punkti koordinaat - antud lõigu keskpunkt

Õpikutöö: §19, lk 112, A. nr 573, 575 B. nr 578, 580 Kodutöö: §19, lk 112, A. nr 574, 576, V. nr 579, 581 valmistuda CR "Ratsionaalarvude liitmine ja lahutamine. Koordinaatjoone punktide vaheline kaugus "

Täna õppisin… See oli huvitav… Sain aru, et… Nüüd saan… Õppisin… Õppisin… Ma proovin… Ma olin üllatunud… Tahtsin…

Käesolevas artiklis vaatleme võimalusi, kuidas teoreetiliselt ja konkreetsete ülesannete näitel määrata kaugust punktist punktini. Alustame mõne definitsiooniga.

Definitsioon 1

Punktide vaheline kaugus- see on neid ühendava lõigu pikkus olemasolevas skaalas. Selleks, et mõõtmiseks oleks pikkusühik, on vaja seadistada skaala. Seetõttu lahendatakse punktidevahelise kauguse leidmise probleem põhimõtteliselt, kasutades nende koordinaate koordinaatjoonel, koordinaattasandil või kolmemõõtmelises ruumis.

Algandmed: koordinaatsirge O x ja sellel asuv suvaline punkt A. Üks reaalarv on omane igale sirge punktile: olgu see punkti A kindel arv xA, see on punkti A koordinaat.

Üldiselt võib öelda, et teatud lõigu pikkuse hindamine toimub võrdluses lõiguga, mis on võetud antud skaalal pikkuseühikuna.

Kui punkt A vastab täisarvulisele reaalarvule, olles eraldanud punktist O punktist O punkti piki sirget O A lõigud - pikkuseühikud, saame lõigu O A pikkuse määrata pooleliolevate üksikute lõikude koguarvu järgi.

Näiteks punkt A vastab numbrile 3 - punktist O sinna jõudmiseks on vaja kõrvale jätta kolm ühiku segmenti. Kui punkti A koordinaat on -4, joonistatakse üksikud lõigud sarnaselt, kuid erinevas negatiivses suunas. Seega on esimesel juhul kaugus O A 3; teisel juhul O A \u003d 4.

Kui punkti A koordinaadiks on ratsionaalarv, siis lähtepunktist (punktist O) jätame kõrvale täisarv ühikulisi segmente ja seejärel selle vajaliku osa. Kuid geomeetriliselt ei ole alati võimalik mõõta teha. Näiteks tundub, et koordinaatide otsemurdu 4 111 kõrvale jätta on keeruline.

Ülaltoodud viisil on täiesti võimatu sirgjoonel irratsionaalset arvu edasi lükata. Näiteks kui punkti A koordinaat on 11 . Sel juhul on võimalik pöörduda abstraktsiooni poole: kui punkti A antud koordinaat on suurem kui null, siis O A \u003d x A (arv võetakse vahemaaks); kui koordinaat on väiksem kui null, siis O A = - x A . Üldiselt on need väited tõesed mis tahes reaalarvu x A kohta.

Kokkuvõtteks: kaugus lähtepunktist punktini, mis vastab koordinaatjoone reaalarvule, on võrdne:

  • 0, kui punkt on lähtepunktiga sama;
  • x A, kui x A > 0;
  • - x A, kui x A< 0 .

Sel juhul on ilmne, et lõigu enda pikkus ei saa olla negatiivne, seetõttu kirjutame mooduli märgi abil koordinaadiga kauguse punktist O punkti A. x A: O A = x A

Õige väide oleks: kaugus ühest punktist teise on võrdne koordinaatide erinevuse mooduliga. Need. punktide A ja B jaoks, mis asuvad mis tahes kohas samal koordinaatjoonel ja millel on vastavalt koordinaadid x A ja x B: A B = x B - x A .

Algandmed: punktid A ja B, mis asuvad tasapinnal ristkülikukujulises koordinaatsüsteemis O x y etteantud koordinaatidega: A (x A , y A) ja B (x B , y B) .

Joonistame koordinaattelgedele O x ja O y läbi punktide A ja B ristid ning saame tulemuseks projektsioonipunktid: A x , A y , B x , B y . Sõltuvalt punktide A ja B asukohast on võimalikud järgmised valikud:

Kui punktid A ja B langevad kokku, on nende vaheline kaugus null;

Kui punktid A ja B asuvad sirgel, mis on risti O x teljega (abstsisstell), siis punktid ja langevad kokku ja | A B | = | A y B y | . Kuna punktide vaheline kaugus on võrdne nende koordinaatide erinevuse mooduliga, siis A y B y = y B - y A ja seega A B = A y B y = y B - y A .

Kui punktid A ja B asuvad sirgel, mis on risti O y-teljega (y-telg) - analoogselt eelmise lõiguga: A B = A x B x = x B - x A

Kui punktid A ja B ei asu sirgel, mis on risti ühe koordinaatteljega, leiame nendevahelise kauguse arvutusvalemi tuletamise teel:

Näeme, et kolmnurk A B C on konstruktsiooni järgi täisnurkne. Sel juhul A C = A x B x ja B C = A y B y . Kasutades Pythagorase teoreemi, koostame võrdsuse: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 ja seejärel teisendame selle: A B = A x B x 2 + A y B y 2 = x B - x A 2 + y B - y A 2 = (x B - x A) 2 + (y B - y A) 2

Saadud tulemusest teeme järelduse: kaugus punktist A punkti B tasapinnal määratakse arvutamise teel valemi abil, kasutades nende punktide koordinaate

A B = (x B - x A) 2 + (y B - y A) 2

Saadud valem kinnitab ka eelnevalt moodustatud väiteid punktide või olukordade kokkulangemise juhtudel, kui punktid asuvad telgedega risti asetsevatel sirgtel. Seega on punktide A ja B kokkulangemise korral võrdsus tõene: A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + 0 2 = 0

Olukorras, kus punktid A ja B asuvad sirgel, mis on risti x-teljega:

A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + (y B - y A) 2 = y B - y A

Juhul, kui punktid A ja B asuvad sirgel, mis on risti y-teljega:

A B = (x B - x A) 2 + (y B - y A) 2 = (x B - x A) 2 + 0 2 = x B - x A

Algandmed: ristkülikukujuline koordinaatsüsteem O x y z, millel asuvad suvalised punktid antud koordinaatidega A (x A , y A , z A) ja B (x B , y B , z B) . On vaja kindlaks määrata nende punktide vaheline kaugus.

Vaatleme üldist juhtumit, kui punktid A ja B ei asu ühe koordinaattasandiga paralleelsel tasapinnal. Joonestage läbi koordinaattelgedega risti olevad punktid A ja B tasapinnad ja saate vastavad projektsioonipunktid: A x , A y , A z , B x , B y , B z

Punktide A ja B vaheline kaugus on saadud kasti diagonaal. Vastavalt selle kasti mõõtmise konstruktsioonile: A x B x , A y B y ja A z B z

Geomeetria käigust on teada, et rööptahuka diagonaali ruut võrdub selle mõõtmete ruutude summaga. Selle väite põhjal saame võrdsuse: A B 2 \u003d A x B x 2 + A y B y 2 + A z B z 2

Kasutades varem tehtud järeldusi, kirjutame järgmise:

A x B x = x B - x A , A y B y = y B - y A , A z B z = z B - z A

Teisendame väljendit:

A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B - x A 2 + y B - y A 2 + z B - z A 2 = = (x B - x A) 2 + (y B - y A) 2 + z B - z A 2

Lõplik valem ruumipunktide vahelise kauguse määramiseks näeb välja selline:

A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2

Saadud valem kehtib ka juhtudel, kui:

Täpid sobivad;

Need asuvad samal koordinaatteljel või sirgel, mis on paralleelne ühe koordinaatteljega.

Näited ülesannete lahendamisest punktidevahelise kauguse leidmiseks

Näide 1

Algandmed: on antud koordinaatjoon ja sellel asuvad punktid antud koordinaatidega A (1 - 2) ja B (11 + 2). On vaja leida kaugus võrdluspunktist O punktini A ning punktide A ja B vahel.

Lahendus

  1. Kaugus võrdluspunktist punktini on võrdne selle punkti koordinaadi mooduliga, vastavalt O A \u003d 1 - 2 \u003d 2 - 1
  2. Punktide A ja B vaheline kaugus on määratletud kui nende punktide koordinaatide erinevuse moodul: A B = 11 + 2 - (1 - 2) = 10 + 2 2

Vastus: O A = 2 - 1, A B = 10 + 2 2

Näide 2

Algandmed: antud ristkülikukujuline koordinaatsüsteem ja sellel asuvad kaks punkti A (1 , - 1) ja B (λ + 1 , 3). λ on mingi reaalarv. On vaja leida kõik selle arvu väärtused, mille puhul kaugus A B võrdub 5-ga.

Lahendus

Punktide A ja B vahelise kauguse leidmiseks peate kasutama valemit A B = (x B - x A) 2 + y B - y A 2

Asendades koordinaatide tegelikud väärtused, saame: A B = (λ + 1 - 1) 2 + (3 - (- 1)) 2 = λ 2 + 16

Ja samuti kasutame olemasolevat tingimust, et A B = 5 ja siis on võrdsus tõene:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Vastus: A B \u003d 5, kui λ \u003d ± 3.

Näide 3

Algandmed: antud on kolmemõõtmeline ruum ristkülikukujulises koordinaatsüsteemis O x y z ja selles asuvad punktid A (1 , 2 , 3) ​​ja B - 7 , - 2 , 4.

Lahendus

Ülesande lahendamiseks kasutame valemit A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2

Asendades tegelikud väärtused, saame: A B = (- 7 - 1) 2 + (- 2 - 2) 2 + (4 - 3) 2 = 81 = 9

Vastus: | A B | = 9

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Tunniplaan.

Kahe sirge punkti vaheline kaugus.

Ristkülikukujuline (Cartesiuse) koordinaatsüsteem.

Kahe sirge punkti vaheline kaugus.

3. teoreem. Kui A(x) ja B(y) on mis tahes kaks punkti, siis d - nendevaheline kaugus arvutatakse valemiga: d = lу - xl.

Tõestus. Vastavalt teoreemile 2 on meil AB = y - x. Kuid punktide A ja B vaheline kaugus on võrdne lõigu AB pikkusega, need. vektori AB pikkus . Seetõttu d \u003d lABl \u003d lu-xl.

Kuna arvud y-x ja x-y on võetud moodulina, saame kirjutada d =lx-ul. Niisiis, koordinaatjoone punktide vahelise kauguse leidmiseks peate leidma nende koordinaatide erinevuse mooduli.

Näide 4. Leidke punktide A(2) ja B(-6) vaheline kaugus.

Lahendus. Asendage valemis x=2 ja y=-6 asemel. Saame, AB=lу-хl=l-6-2l=l-8l=8.

Näide 5 Ehitage punkt, mis on algpunkti suhtes sümmeetriline punktiga M(4).

Lahendus. Sest punktist M punkti O 4 üksikut segmenti, jätke paremale kõrvale, seejärel, et ehitada sellele sümmeetriline punkt, lükkame punktist O 4 üksikut lõiku vasakule, saame punkti M "( -4).

Näide 6 Koostage punkt C(x), mis on sümmeetriline punktiga A(-4) punkti B(2) suhtes.

Lahendus. Märkige arvureal olevad punktid A(-4) ja B(2). Punktide vahelise kauguse leiame teoreemi 3 järgi, saame 6. Siis peaks punktide B ja C vaheline kaugus olema samuti võrdne 6-ga. Asetame punktist B paremale 6 ühikulist lõiku, saame punkti C (8) .

Harjutused. 1) Leidke punktide A ja B vaheline kaugus: a) A(3) ja B(11), b) A(5) ja B(2), c) A(-1) ja B(3), d) A (-5) ja B (-3), e) A (-1) ja B (3), (vastus: a) 8, b) 3, c) 4, d) 2, e) 2).

2) Ehitage punkt C(x), mis on sümmeetriline punktiga A(-5) punkti B(-1) suhtes. (Vastus: C(3)).

Ristkülikukujuline (Cartesiuse) koordinaatsüsteem.

Moodustavad kaks vastastikku risti asetsevat telge Ox ja Oy, millel on ühine alguspunkt O ja sama mõõtkava. ristkülikukujuline(või Descartes) koordinaatide süsteem tasapinnal.

Ox telge nimetatakse x-telg ja y-telg y-telg. Telgede lõikepunkti O nimetatakse päritolu. Tasapinda, millel asuvad teljed Ox ja Oy, nimetatakse koordinaattasandiks ja tähistatakse Oxy-ga.

Olgu M tasapinna suvaline punkt. Loobume sellest telgedel Ox ja Oy vastavalt ristid MA ja MB. Nimetatakse kummagi risti telgedega lõikepunktid A ja B prognoosid punkti M koordinaatteljel.

Punktid A ja B vastavad teatud arvudele x ja y – nende koordinaadid telgedel Ox ja Oy. Numbrit x kutsutakse abstsiss punktid M, number y - tema ordinaat.

Seda, et punktil M on koordinaadid x ja y, tähistatakse sümboolselt järgmiselt: M(x, y). Sel juhul tähistab esimene sulgudes abstsissi ja teine ​​- ordinaati. Algpunktil on koordinaadid (0,0).

Seega vastab valitud koordinaatsüsteemi iga tasandi punkt M numbripaarile (x, y) - selle ristkülikukujulised koordinaadid ja vastupidi, igale numbripaarile (x, y) ja pealegi üks punkt. M Oxy-tasandil nii, et selle abstsiss on x ja ordinaat on y.

Niisiis loob tasapinna ristkülikukujuline koordinaatsüsteem üks-ühele vastavuse tasandi kõigi punktide hulga ja arvupaaride hulga vahel, mis võimaldab geomeetriliste ülesannete lahendamisel rakendada algebralisi meetodeid.

Koordinaatide teljed jagavad tasapinna neljaks osaks, neid nimetatakse veerandid, kvadrandid või koordinaatnurgad ja nummerdatud rooma numbritega I, II, III, IV, nagu on näidatud joonisel (hüperlink).

Joonisel on näha ka punktide koordinaatide märgid sõltuvalt nende asukohast. (näiteks I kvartalis on mõlemad koordinaadid positiivsed).

Näide 7 Ehituspunktid: A(3;5), B(-3;2), C(2;-4), D (-5;-1).

Lahendus. Konstrueerime punkti A(3;5). Kõigepealt tutvustame ristkülikukujulist koordinaatsüsteemi. Seejärel paneme mööda abstsisstellge kõrvale 3 mõõtkava ühikut paremale ja piki ordinaattelge 5 mõõtkava ühikut ülespoole ning läbi lõplike jaotuspunktide tõmbame koordinaatide telgedega paralleelsed sirgjooned. Nende sirgete lõikepunktiks on nõutav punkt A(3;5). Ülejäänud punktid konstrueeritakse samamoodi (vt hüperlingi joonist).

Harjutused.

    Joonista punkti A(2;-4) välja, millisesse kvartalisse see kuulub.

    Millistel veeranditel võib punkt olla, kui selle ordinaat on positiivne?

    Oy teljel võetakse punkt koordinaadiga -5. Mis on selle koordinaadid lennukis? (vastus: kuna punkt asub Oy teljel, siis selle abstsiss on 0, ordinaat on antud tingimusega, seega punkti koordinaadid on (0; -5)).

    Punkte antakse: a) A(2;3), b) B(-3;2), c) C(-1;-1), d) D(x;y). Leidke nende punktide koordinaadid, mis on x-telje suhtes sümmeetrilised. Joonistage kõik need punktid. (vastus: a) (2; -3), b) (-3; -2), c) (-1; 1), d) (x; -y)).

    Punkte antakse: a) A(-1;2), b) B(3;-1), c) C(-2;-2), d) D(x;y). Leia nende punktide koordinaadid, mis on y-telje suhtes sümmeetrilised. Joonistage kõik need punktid. (vastus: a) (1; 2), b) (-3; -1), c) (2; -2), d) (-x; y)).

    Punkte antakse: a) A(3;3), b) B(2;-4), c) C(-2;1), d) D(x;y). Leidke nende punktide koordinaadid, mis on nende algpunkti suhtes sümmeetrilised. Joonistage kõik need punktid. (vastus: a) (-3; -3), b) (-2; 4), c) (2; -1), d) (-x;-y)).

    Antud punkt M(3;-1). Leidke punktide koordinaadid, mis on sellega sümmeetrilised Ox-telje, Oy-telje ja alguspunkti suhtes. Joonistage kõik punktid. (vastus: (3;1), (-3;-1), (-3;1)).

    Määrake, millistes kvartalites võib punkt M (x; y) paikneda, kui: a) xy> 0, b) xy< 0, в) х-у=0, г) х+у=0. (ответ: а) в первой и третьей, б)во второй и четвертой, в) в первой и третьей, г) во второй и четвертой).

    Määrake võrdkülgse kolmnurga tippude koordinaadid, mille külg on 10 ja mis asub esimeses kvadrandis, kui üks selle tippudest langeb kokku lähtepunktiga O ja kolmnurga alus asub Ox-teljel. Tee joonistus. (vastus: (0;0), (10;0), (5;5v3)).

    Koordinaatide meetodil määrake korrapärase kuusnurga ABCDEF kõigi tippude koordinaadid. (vastus: A (0;0), B (1;0), C (1,5;v3/2) , D (1;v3), E (0;v3), F (-0,5;v3 /2). Näidus: võtke koordinaatide alguspunktiks punkt A, suunake abstsisstelg punktist A punkti B, võtke mõõtkava ühikuks külje AB pikkus. Kuusnurgale on mugav joonistada suuri diagonaale.)


Kaugus punktist punkti on neid punkte ühendava segmendi pikkus antud skaalal. Seega on kauguse mõõtmisel vaja teada skaalat (pikkusühikut), milles mõõtmised tehakse. Seetõttu käsitletakse punktist punkti kauguse leidmise probleemi tavaliselt kas koordinaatsirge või ristkülikukujulises Descartes'i koordinaatsüsteemis tasapinnal või kolmemõõtmelises ruumis. Teisisõnu, kõige sagedamini peate arvutama punktide vahelise kauguse nende koordinaatide järgi.

Selles artiklis tuletame esiteks meelde, kuidas määratakse kaugus punktist koordinaatjoone punktini. Järgmiseks saame valemid tasandi või ruumi kahe punkti vahelise kauguse arvutamiseks etteantud koordinaatide järgi. Kokkuvõtteks käsitleme üksikasjalikult tüüpiliste näidete ja probleemide lahendusi.

Leheküljel navigeerimine.

Kahe koordinaatjoone punkti vaheline kaugus.

Kõigepealt defineerime tähistus. Kaugus punktist A punkti B tähistatakse kui .

Sellest võime järeldada, et kaugus koordinaadiga punktist A koordinaadiga punktini B on võrdne koordinaatide erinevuse mooduliga, see on, punktide mis tahes paigutuse jaoks koordinaatjoonel.

Kaugus punktist punktini tasapinnal, valem.

Võtame valemi punktide vahelise kauguse arvutamiseks ja antud ristkülikukujulises Descartes'i koordinaatsüsteemis tasapinnal.

Sõltuvalt punktide A ja B asukohast on võimalikud järgmised valikud.

Kui punktid A ja B langevad kokku, on nende vaheline kaugus null.

Kui punktid A ja B asuvad sirgel, mis on risti x-teljega, siis punktid ja langevad kokku ning kaugus võrdub kaugusega. Eelmises lõigus saime teada, et kahe koordinaatjoone punkti vaheline kaugus on võrdne nende koordinaatide erinevuse mooduliga, seega . Järelikult,.

Samamoodi, kui punktid A ja B asuvad sirgel, mis on risti y-teljega, siis kaugus punktist A punkti B leitakse kui .

Sel juhul on kolmnurk ABC ehituselt ristkülikukujuline ja ja . Kõrval Pythagorase teoreem saame kirjutada võrdsuse , kust .

Võtame kõik tulemused kokku: kaugus punktist tasapinna punktini leitakse punktide koordinaatide kaudu valemiga .

Saadud valemit punktidevahelise kauguse leidmiseks saab kasutada siis, kui punktid A ja B langevad kokku või asuvad sirgel, mis on risti ühe koordinaatteljega. Tõepoolest, kui A ja B on samad, siis . Kui punktid A ja B asuvad sirgel, mis on risti Ox-teljega, siis . Kui A ja B asuvad Oy teljega risti asetseval sirgel, siis .

Ruumipunktide vaheline kaugus, valem.

Tutvustame ruumis ristkülikukujulist koordinaatsüsteemi Оxyz. Hankige punktist kauguse leidmise valem asja juurde .

Üldjuhul ei asu punktid A ja B ühe koordinaattasandiga paralleelsel tasapinnal. Joonistame punktid A ja B läbi koordinaattelgedega Ox, Oy ja Oz risti oleva tasapinna. Nende tasandite lõikepunktid koordinaattelgedega annavad meile punktide A ja B projektsioonid nendel telgedel. Tähistage projektsioone .


Soovitud kaugus punktide A ja B vahel on joonisel kujutatud ristkülikukujulise rööptahuka diagonaal. Konstruktsiooni järgi on selle rööptahuka mõõtmed ja . Gümnaasiumi geomeetria kursusel tõestati, et ristkülikukujulise rööptahuka diagonaali ruut on võrdne tema kolme mõõtme ruutude summaga, seega. Selle artikli esimese jaotise teabe põhjal saame kirjutada järgmised võrdsused, seega

kuhu me jõuame valem ruumipunktide vahelise kauguse leidmiseks .

See valem kehtib ka punktide A ja B korral

  • vaste;
  • kuuluvad ühte koordinaattelgedest või sirge, mis on paralleelne ühe koordinaatteljega;
  • kuuluvad ühele koordinaattasanditest või ühe koordinaattasandiga paralleelsele tasapinnale.

Punkti kauguse leidmine, näited ja lahendused.

Niisiis, oleme saanud valemid koordinaatjoone, tasandi ja kolmemõõtmelise ruumi kahe punkti vahelise kauguse leidmiseks. On aeg kaaluda tüüpiliste näidete lahendusi.

Probleemide arv, mille puhul viimaseks sammuks on kahe punkti vahelise kauguse leidmine nende koordinaatide järgi, on tõesti tohutu. Selliste näidete täielik ülevaade ei kuulu käesoleva artikli ulatusse. Siin piirdume näidetega, mille puhul on teada kahe punkti koordinaadid ja on vaja arvutada nendevaheline kaugus.

Sarnased artiklid