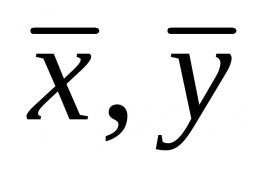Juhuslike suuruste vahelise lineaarse seose tihedus. Juhuslike suuruste vahelise seose tiheduse määramine

13.07.2020

Regressioonianalüüs

Katse tulemuste töötlemine meetodil

Keeruliste süsteemide toimimisprotsesse uurides tuleb tegeleda mitmete samaaegselt toimivate juhuslike suurustega. Et mõista nähtuste mehhanismi, põhjus-tagajärg seoseid süsteemi elementide vahel jne, püüame saadud vaatluste põhjal nende suuruste seost tuvastada.

AT matemaatiline analüüs sõltuvust näiteks kahe suuruse vahel väljendab funktsiooni mõiste

kus ühe muutuja iga väärtus vastab ainult teise ühele väärtusele. Seda sõltuvust nimetatakse funktsionaalne.

Juhuslike suuruste sõltuvuse mõistega on olukord palju keerulisem. Tavaliselt vahel juhuslikud muutujad(juhuslikud tegurid), mis määravad keerukate süsteemide toimimise protsessi, on tavaliselt selline seos, kus ühe suuruse muutumisel muutub teise jaotus. Sellist ühendust nimetatakse stohhastiline, või tõenäosuslik. Sel juhul juhusliku teguri muutuse suurus Y, mis vastab väärtuse muutusele X, võib jagada kaheks komponendiks. Esimene on seotud sõltuvusega. Y alates X, ja teine "oma" juhuslike komponentide mõjul Y ja X. Kui esimene komponent puudub, siis juhuslikud muutujad Y ja X on iseseisvad. Kui teine komponent puudub, siis Y ja X sõltuvad funktsionaalselt. Mõlema komponendi olemasolul määrab nendevaheline suhe juhuslike suuruste vahelise seose tugevuse või tiheduse Y ja X.

Stohhastilise seose teatud aspekte iseloomustavad erinevad näitajad. Niisiis, lineaarne sõltuvus juhuslike muutujate vahel X ja Y määrab korrelatsioonikordaja.

kus on juhuslike suuruste X matemaatilised ootused ja Y.

– juhuslike suuruste standardhälbed X ja Y.

Juhuslike suuruste lineaarne tõenäosussõltuvus seisneb selles, et ühe juhusliku suuruse kasvades kipub teine lineaarse seaduse kohaselt kasvama (või vähenema). Kui juhuslikud muutujad X ja Y on ühendatud range lineaarse funktsionaalse sõltuvusega, näiteks

y = b 0 + b 1 x 1,

siis on korrelatsioonikordaja võrdne ; kus märk vastab koefitsiendi märgile b 1.Kui väärtused X ja Y on ühendatud suvalise stohhastilise sõltuvusega, siis varieerub korrelatsioonikordaja piires

Tuleb rõhutada, et sõltumatute juhuslike muutujate korral on korrelatsioonikordaja võrdne nulliga. Korrelatsioonikoefitsiendil kui juhuslike muutujate vahelise sõltuvuse indikaatoril on aga tõsiseid puudusi. Esiteks võrdsusest r= 0 ei tähenda juhuslike muutujate sõltumatust X ja Y(välja arvatud juhuslikud suurused, mille suhtes kehtib normaaljaotuse seadus, mille puhul r= 0 tähendab samal ajal igasuguse sõltuvuse puudumist). Teiseksäärmuslikud väärtused pole samuti eriti kasulikud, kuna need ei vasta ühelegi funktsionaalsele sõltuvusele, vaid ainult rangelt lineaarsele sõltuvusele.

Täielik kirjeldus sõltuvused Y alates X, ja pealegi väljendatuna täpsetes funktsionaalsetes suhetes, saab saada tingimusliku jaotuse funktsiooni tundmisega.

Tuleb märkida, et sel juhul peetakse üht vaadeldud muutujatest mittejuhuslikuks. Kahe juhusliku muutuja väärtuste samaaegne fikseerimine X ja Y, kui nende väärtusi võrrelda, saame kõik vead omistada ainult väärtusele Y. Seega on vaatlusviga tema enda juhusliku koguse vea summa Y ja sobitusveast, mis tuleneb asjaolust, et väärtusega Y ei sobi päris sama väärtus X mis tegelikult toimus.

Tingimusliku jaotusfunktsiooni leidmine osutub aga reeglina väga keeruliseks ülesandeks. Lihtsaim viis vaheliste seoste uurimiseks X ja Y normaaljaotusega Y, kuna see on täielikult määratud matemaatilise ootuse ja dispersiooniga. Antud juhul sõltuvuse kirjeldamiseks Y alates X parameetri muutmisel ei pea ehitama tingimusjaotusfunktsiooni, vaid lihtsalt näitama, kuidas X väärtuse muutumise matemaatiline ootus ja dispersioon Y.

Seega jõuame vajaduseni leida ainult kaks funktsiooni:

Tingimuslik dispersioonisõltuvus D parameetrist X kutsutakse skhodastichesky sõltuvused. See iseloomustab vaatlustehnika täpsuse muutumist parameetri muutumisega ja seda kasutatakse üsna harva.

Tingimusliku matemaatilise ootuse sõltuvus M alates X kutsutakse regressioon, annab see koguste tõelise sõltuvuse X ja Kell, millel puuduvad kõik juhuslikud kihid. Seetõttu on iga sõltuvate muutujate uurimise ideaalne eesmärk regressioonivõrrandi leidmine ja dispersiooni kasutatakse ainult tulemuse täpsuse hindamiseks.

Korrelatsioon-kahe või enama juhusliku muutuja statistiline seos.

Osakorrelatsioonikordaja iseloomustab kahe suuruse lineaarse seose astet, omab kõiki paari omadusi, s.t. varieerub vahemikus -1 kuni +1. Kui osakorrelatsioonikordaja on ±1, siis on kahe suuruse vaheline seos funktsionaalne ja selle võrdsus nulliga näitab lineaarne iseseisvus need kogused.

Mitmekordne korrelatsioonikordaja iseloomustab lineaarse sõltuvuse astet väärtuse x 1 ja teiste mudelis sisalduvate muutujate (x 2, x s) vahel, varieerub vahemikus 0 kuni 1.

Ordinaal (järguline) muutuja aitab sorteerida statistiliselt uuritud objekte vastavalt analüüsitava omaduse avaldumisastmele neis

Astekorrelatsioon – statistiline seos järgmuutujate vahel (statistilise seose mõõtmine kahe või enama sama lõpliku objektide kogumi O 1, O 2, ..., O p. vahel)

pingerida on objektide paigutus nendes uuritava k-nda omaduse avaldumisastme kahanevas järjekorras. Sel juhul nimetatakse x(k) i-nda objekti auastmeks k-nda tunnuse järgi. Raev iseloomustab objekti O i järjekorrakohta n objektist koosnevas reas.

39. Korrelatsioonikordaja, määramine.

Korrelatsioonikordaja näitab kahe arvmuutuja statistilise sõltuvuse määr. See arvutatakse järgmiselt:

kus n– vaatluste arv,

x on sisendmuutuja,

y on väljundmuutuja. Korrelatsioonikordaja väärtused on alati vahemikus -1 kuni 1 ja neid tõlgendatakse järgmiselt:

kui koefitsient korrelatsioon on 1-le lähedane, siis on muutujate vahel positiivne korrelatsioon.

kui koefitsient korrelatsioon on -1 lähedal, mis tähendab, et muutujate vahel on negatiivne korrelatsioon

0-le lähedased vahepealsed väärtused näitavad nõrka korrelatsiooni muutujate vahel ja vastavalt madalat sõltuvust.

Määramise koefitsient (R 2 )- see on sõltuva muutuja keskmisest kõrvalekallete seletatud dispersiooni osakaal.

Määramiskoefitsiendi arvutamise valem:

R 2 \u003d 1 - ∑ i (y i -f i) 2 : ∑ i (y i -y(kriips)) 2

Kui y i on sõltuva muutuja vaadeldav väärtus ja f i on regressioonivõrrandiga ennustatud sõltuva muutuja väärtus, siis y(kriips) on sõltuva muutuja aritmeetiline keskmine.

16. küsimus

Selle meetodi kohaselt kasutatakse järgmise Tarnija varusid järgmiste Tarbijate vajaduste rahuldamiseks kuni nende täieliku ammendumiseni. Pärast seda kasutatakse numbri järgi järgmise Tarnija varusid.

Transpordiülesande tabeli täitmine algab ülemisest vasakust nurgast ja koosneb mitmest sama tüüpi sammust. Igal etapil täidetakse järgmise Tarnija laoseisude ja järgmise Tarbija taotluste alusel ainult üks lahter ja vastavalt sellele jäetakse üks Tarnija või Tarbija vaatlusest välja.

Vigade vältimiseks tuleb pärast esialgse põhi- (referents)lahenduse koostamist kontrollida, et hõivatud lahtrite arv oleks võrdne m + n-1.

Muudatuste 7 ja X vahel. Juhuslike suuruste vaheliste seoste läheduse hindamiseks kasutatakse näitajaid

Nagu juba öeldud, on üks peamisi erinevusi aegrida moodustavate vaatluste jada vahel selles, et aegrea liikmed on üldiselt statistiliselt üksteisest sõltuvad. Juhuslike suuruste Xt ja Xt + T vahelise statistilise seose tiheduse astet saab mõõta paaripõhise korrelatsioonikordaja abil

Üldparameetri hinnang saadakse valiminäitaja alusel, võttes arvesse esindusviga. Teisel juhul, seoses üldkogumi omadustega, püstitatakse mingi hüpotees keskmise väärtuse, dispersiooni, jaotuse olemuse, muutujatevahelise seose vormi ja läheduse kohta. Hüpoteesi kontrollimine toimub empiiriliste andmete ja hüpoteetiliste (teoreetiliste) andmete kooskõla tuvastamise alusel. Kui võrreldavate väärtuste lahknevus ei ületa juhuslike vigade piire, aktsepteeritakse hüpotees. Hüpoteesi enda õigsuse kohta aga järeldusi ei tehta, me räägime ainult võrreldavate andmete järjepidevuse kohta. Statistiliste hüpoteeside kontrollimise aluseks on juhuslike valimite andmed. Pole vahet, kas hüpoteese hinnatakse tegeliku või hüpoteetilise populatsiooni suhtes. Viimane avab võimaluse selle meetodi rakendamiseks väljaspool tegelikku valimit, analüüsides katse tulemusi, pideva vaatluse andmeid, kuid vähesel määral. Sel juhul on soovitatav kontrollida, kas väljakujunenud seaduspärasus on põhjustatud juhuslike asjaolude koosmõjust, mil määral on see tüüpiline tingimuste kompleksile, milles uuritav populatsioon paikneb.

Selgub, et skeemi (, m]) korrelatsiooni- ja regressioonikarakteristikud võivad oluliselt erineda algse (moonutamata) skeemi vastavatest karakteristikutest (, n). Algse kahemõõtmelise normaalskeemi normaalvead (, m) vähendab alati regressioonikordaja Ql absoluutväärtust suhtes (B. 15), samuti nõrgendab u vahelise seose tiheduse astet (s.t. vähendab korrelatsioonikordaja r absoluutväärtust).

Mõõtmisvigade mõju korrelatsioonikordaja väärtusele. Tahame hinnata kahemõõtmelise normaaljuhusliku suuruse (, TJ) komponentide vahelise korrelatsiooni lähedusastet, kuid neid saab jälgida ainult mõne juhusliku mõõtmisveaga, vastavalt es ja e (vt skeemi sõltuvus D2 sissejuhatuses). Seetõttu on katseandmed (xit i/i), i = 1, 2,. .., n on praktiliselt moonutatud kahemõõtmelise juhusliku suuruse (, r) näidisväärtused, kus =

Meetod R.a. seisneb regressioonivõrrandi (sh selle parameetrite hinnangu) tuletamises, mille abil leitakse juhusliku suuruse keskmine väärtus, kui on teada teise (mitme- või mitme muutujaga regressiooni korral ka teiste) väärtus. (Seevastu korrelatsioonianalüüsi kasutatakse juhuslike muutujate vahelise seose tugevuse leidmiseks ja väljendamiseks71.)

Nende tunnuste korrelatsiooni uurimisel, mis ei ole seotud järjepideva muutumisega ajas, muutub iga tunnus paljude põhjuste mõjul, võttes arvesse juhuslikku. Dünaamika seerias lisandub neile muudatus iga seeria aja jooksul. See muutus viib nn autokorrelatsioonini - eelmiste seeriate tasemete muutuste mõju järgmistele. Seetõttu näitab aegridade tasemete vaheline korrelatsioon õigesti aegreas kajastuvate nähtuste vahelise seose tihedust vaid juhul, kui autokorrelatsioon neist igaühes puudub. Lisaks põhjustab autokorrelatsioon regressioonikordajate keskmiste ruutvigade moonutamist, mis muudab regressioonikordajate usaldusvahemike koostamise ja nende olulisuse kontrollimise keeruliseks.

Vastavalt seostega (1.8) ja (1.8) defineeritud teoreetilised ja valimikorrelatsioonikordajad on formaalselt arvutatavad mis tahes kahemõõtmelise vaatlussüsteemi jaoks, need on analüüsitavate tunnuste vahelise lineaarse statistilise seose lähedusastme mõõdikud. Kuid ainult uuritavate juhuslike suuruste ja u ühise normaaljaotuse korral on korrelatsioonikordajal r selge tähendus nendevahelise seose lähedusastme tunnusena. Eelkõige kinnitab sel juhul suhe r - 1 puhtfunktsionaalset lineaarset seost uuritavate suuruste vahel ja võrrand r = 0 näitab nende täielikku vastastikust sõltumatust. Lisaks moodustab korrelatsioonikordaja koos juhuslike suuruste ja TJ keskmiste ja dispersioonidega need viis parameetrit, mis annavad igakülgset teavet

Seos, mis eksisteerib erineva iseloomuga juhuslike muutujate vahel, näiteks X väärtuse ja Y väärtuse vahel, ei pruugi olla ühe muutuja otsese sõltuvuse tagajärg teisest (nn funktsionaalne seos). Mõningatel juhtudel sõltuvad mõlemad suurused tervest komplektist erinevatest mõlemale suurusele ühistest teguritest, mille tulemusena tekivad üksteisega seotud mustrid. Kui statistika abil avastatakse juhuslike muutujate vaheline seos, ei saa me väita, et oleme avastanud parameetrite pideva muutumise põhjuse, pigem nägime ainult kahte omavahel seotud tagajärge.

Näiteks lapsed, kes vaatavad televiisorist rohkem Ameerika märulifilme, loevad vähem. Lapsed, kes loevad rohkem, õpivad paremini. Ei ole nii lihtne otsustada, millised on põhjused ja millised tagajärjed, kuid see pole statistika ülesanne. Statistika saab esitada ainult hüpoteesi ühenduse olemasolu kohta, seda numbritega kinnitada. Kui seos on tõepoolest olemas, siis öeldakse, et need kaks juhuslikku muutujat on korrelatsioonis. Kui ühe juhusliku suuruse suurenemist seostatakse teise juhusliku suuruse suurenemisega, nimetatakse korrelatsiooni otseseks. Näiteks loetud lehekülgede arv aastas ja keskmine punktisumma (sooritus). Kui vastupidi, ühe väärtuse suurenemine on seotud teise vähenemisega, siis räägitakse pöördkorrelatsioonist. Näiteks märulifilmide arv ja loetud lehekülgede arv.

Kahe juhusliku muutuja omavahelist seost nimetatakse korrelatsiooniks, korrelatsioonianalüüs võimaldab määrata sellise seose olemasolu, hinnata, kui tihe ja oluline see seos on. Kõik see on kvantifitseeritud.

Kuidas teha kindlaks, kas väärtuste vahel on korrelatsioon? Enamikul juhtudel võib seda näha tavalisel diagrammil. Näiteks saame iga meie valimi lapse jaoks määrata väärtuse X i (lehekülgede arv) ja Y i ( GPA aasta hinnang) ja registreerige need andmed tabelisse. Koostage X- ja Y-telg ning seejärel joonistage graafikule kogu punktide seeria nii, et igaühel neist oleks meie tabelist konkreetne koordinaatide paar (X i , Y i). Kuna sel juhul on meil raske kindlaks teha, mida võib pidada põhjuseks ja mis tagajärjeks, siis pole vahet, milline telg on vertikaalne ja milline horisontaalne.

Kui graafik näeb välja nagu a), näitab see otsese korrelatsiooni olemasolu, kui see näeb välja nagu b) - korrelatsioon on pöördvõrdeline. Korrelatsiooni puudumine
Korrelatsioonikordaja abil saate arvutada, kui tihe seos on väärtuste vahel.

Oletame, et toote hinna ja nõudluse vahel on korrelatsioon. Ostetud kaubaühikute arv olenevalt erinevate müüjate hinnast on näidatud tabelis:

On näha, et tegemist on pöördkorrelatsiooniga. Ühenduse tiheduse kvantifitseerimiseks kasutatakse korrelatsioonikoefitsienti:

Arvutame koefitsiendi r Excelis, kasutades funktsiooni f x, seejärel statistilisi funktsioone, funktsiooni CORREL. Programmi käsul sisestame hiirega kahele vastavale väljale kaks erinevat massiivi (X ja Y). Meie puhul osutus korrelatsioonikordaja r = - 0,988. Tuleb märkida, et mida lähemal on korrelatsioonikordaja 0-le, seda nõrgem on seos väärtuste vahel. Lähim seos otsese korrelatsiooniga vastab koefitsiendile r, mis on lähedane +1-le. Meie puhul on korrelatsioon pöördvõrdeline, aga ka väga lähedane ja koefitsient on -1 lähedal.

Mida saab öelda juhuslike suuruste kohta, mille koefitsiendil on vahepealne väärtus? Näiteks kui saame r=0,65. Sel juhul võimaldab statistika väita, et kaks juhuslikku muutujat on omavahel osaliselt seotud. Oletame, et 65% mõjust ostude arvule avaldas hind ja 35% - muud asjaolud.

Ja tuleks mainida veel üht olulist asjaolu. Kuna me räägime juhuslikest muutujatest, siis on alati võimalus, et meie täheldatud seos on juhuslik asjaolu. Veelgi enam, tõenäosus leida seost seal, kus seda pole, on eriti suur siis, kui valimis on vähe punkte ja hindamisel ei ehitanud te graafikut, vaid arvutasite lihtsalt arvutis korrelatsioonikordaja väärtuse. Niisiis, kui jätame ainult kaks erinevad punktid mis tahes suvalises valimis on korrelatsioonikordaja võrdne kas +1 või -1. Alates koolikursus Geomeetrias teame, et sirge saab alati tõmmata läbi kahe punkti. Avastatud seose fakti statistilise olulisuse hindamiseks on kasulik kasutada nn korrelatsiooniparandust:

Kui korrelatsioonianalüüsi ülesanne on kindlaks teha, kas need juhuslikud suurused on omavahel seotud, siis regressioonanalüüsi eesmärk on kirjeldada seda seost analüütilise sõltuvusega, s.o. võrrandit kasutades. Vaatleme lihtsaimat juhtumit, kui graafiku punktide vahelist seost saab kujutada sirgjoonega. Selle sirge võrrand on Y=aX+b, kus a=Yav.-bXav.,

Teades , võime leida funktsiooni väärtuse argumendi väärtuse järgi nendes punktides, kus X väärtus on teada, aga Y mitte. Need hinnangud on väga kasulikud, kuid nende kasutamisel tuleb olla ettevaatlik, eriti kui koguste seos ei ole liiga tihe.

Samuti märgime, et b ja r valemite võrdlusest on näha, et koefitsient ei anna sirge kalde väärtust, vaid näitab ainult ühenduse olemasolu fakti.

Ettevõttes töötab 10 inimest. Tabelis 2 on toodud andmed nende töökogemuse ja

kuupalk.

Arvutage nende andmete põhjal

- valimi kovariatsioonihinnangu väärtus;
- valimi Pearsoni korrelatsioonikordaja väärtus;
- hinnata saadud väärtuste järgi ühenduse suunda ja tugevust;
- teha kindlaks, kui õigustatud on väide, et see ettevõte kasutab Jaapani juhtimismudelit, mis seisneb eelduses, et mida rohkem aega töötaja selles ettevõttes veedab, seda suurem peaks olema tema palk.

Korrelatsioonivälja põhjal võib oletada (üldpopulatsiooni jaoks), et seos X ja Y kõigi võimalike väärtuste vahel on lineaarne.

Regressiooniparameetrite arvutamiseks koostame arvutustabeli.

Näidis tähendab.

Näidiserinevused:

Hinnanguline regressioonivõrrand näeb välja selline

y = bx + a + e,

kus ei on vigade ei, a ja b vaadeldud väärtused (hinnangud), vastavalt parameetrite b ja regressioonimudeli hinnangud, mis tuleks leida.

Parameetrite b ja c hindamiseks kasutage LSM-i (vähimruutusid).

Normaalvõrrandite süsteem.

a?x + b?x2 = ?y*x

Meie andmete jaoks on võrrandisüsteemil vorm

10a + 307b = 33300
307 a + 10857 b = 1127700

Korrutame süsteemi võrrandi (1) (-30,7), saame süsteemi, mille lahendame algebralise liitmise meetodil.

-307a -9424,9 b = -1022310
307 a + 10857 b = 1127700

Saame:

1432,1b = 105390

kus b = 73,5912

Nüüd leiame võrrandist (1) koefitsiendi "a":

10a + 307b = 33300
10a + 307 * 73,5912 = 33300
10a = 10707,49

Saame empiirilised regressioonikordajad: b = 73,5912, a = 1070,7492

Regressioonivõrrand (empiiriline regressioonivõrrand):

y = 73,5912 x + 1070,7492

kovariatsioon.

Meie näites on seos tunnuse Y ja teguri X vahel kõrge ja otsene.

Seega võib julgelt väita, et mida rohkem aega töötaja antud ettevõttes töötab, seda suurem on tema palk.

4. Statistiliste hüpoteeside kontrollimine. Selle probleemi lahendamisel tuleb kõigepealt sõnastada testitav hüpotees ja alternatiivne hüpotees.

Üldaktsiate võrdsuse kontrollimine.

Kahes teaduskonnas viidi läbi uuring üliõpilaste tulemuslikkuse kohta. Variantide tulemused on toodud tabelis 3. Kas võib väita, et mõlemas teaduskonnas on ühepalju võrratuid üliõpilasi?

lihtne aritmeetiline keskmine

Testime hüpoteesi üldaktsiate võrdsuse kohta:

Leiame Studenti kriteeriumi eksperimentaalse väärtuse:

Vabadusastmete arv

f \u003d nx + ny - 2 = 2 + 2 - 2 \u003d 2

Määrake tkp väärtus Studenti jaotustabeli järgi

Studenti tabeli järgi leiame:

Ttabl(f;b/2) = Ttabl(2;0,025) = 4,303

Studenti jaotuse kriitiliste punktide tabeli järgi olulisuse tasemel b = 0,05 ja etteantud arvu vabadusastmete korral leiame tcr = 4,303

Sest tobs > tcr, siis nullhüpotees lükatakse tagasi, kahe valimi üldised osakaalud ei ole võrdsed.

Üldjaotuse ühtluse kontrollimine.

Ülikooli juhtkond soovib uurida, kuidas on humanitaarteaduskonna populaarsus aja jooksul muutunud. Sellesse teaduskonda kandideerinute arvu analüüsiti vastava aasta sisseastujate üldarvu suhtes. (Andmed on toodud tabelis 4). Kui võtta aasta koolilõpetajate üldarvust esinduslikuks valimiks sisseastujate arv, siis kas võib väita, et kooliõpilaste huvi selle teaduskonna erialade vastu ajas ei muutu?

4. võimalus

Lahendus: Tabel näitajate arvutamiseks.

Intervalli keskpunkt, xi	Kumulatiivne sagedus, S	Sagedus, fi/n

Jaotussarjade hindamiseks leiame järgmised näitajad:

kaalutud keskmine

Variatsioonivahemik on erinevus esmase seeria atribuudi maksimaalse ja minimaalse väärtuse vahel.

R = 2008 - 1988 = 20 Dispersioon - iseloomustab hajuvuse mõõtu selle keskmise väärtuse ümber (dispersiooni mõõt, s.o kõrvalekalle keskmisest).

Standardhälve (keskmine valimiviga).

Iga seeria väärtus erineb 2002. aasta keskmisest väärtusest 66 keskmiselt 6,32 võrra

Üldpopulatsiooni ühtlase jaotuse hüpoteesi testimine.

Selleks, et kontrollida hüpoteesi X ühtlase jaotuse kohta, s.o. seaduse järgi: f(x) = 1/(b-a) intervallis (a,b) on vaja:

Hinnake parameetreid a ja b - selle intervalli lõppu, milles X võimalikke väärtusi täheldati, vastavalt valemitele (* tähistab parameetrite hinnanguid):

Leidke hinnangulise jaotuse f(x) = 1/(b* - a*) tõenäosustihedus

Leia teoreetilised sagedused:

n1 = nP1 = n = n*1/(b* - a*)*(x1 - a*)

n2 = n3 = ... = ns-1 = n*1/(b* - a*)*(xi - xi-1)

ns = n*1/(b* - a*)*(b* - xs-1)

Võrrelge empiirilisi ja teoreetilisi sagedusi Pearsoni testi abil, eeldades vabadusastmete arvu k = s-3, kus s on algsete diskreetimisintervallide arv; kui aga tehti kombinatsioon väikestest sagedustest ja seega ka intervallidest, siis s on pärast kombinatsiooni järelejäänud intervallide arv. Leiame ühtlase jaotuse parameetrite a* ja b* hinnangud valemitega:

Leiame oletatava ühtlase jaotuse tiheduse:

f(x) = 1/(b* - a*) = 1/(2013,62 - 1991,71) = 0,0456

Leiame teoreetilised sagedused:

n1 = n*f(x)(x1 - a*) = 0,77 * 0,0456 (1992-1991,71) = 0,0102

n5 = n*f(x)(b* - x4) = 0,77 * 0,0456 (2013,62-2008) = 0,2

ns = n*f(x)(xi - xi-1)

Kuna Pearsoni statistika mõõdab erinevust empiirilise ja teoreetilise jaotuse vahel, siis mida suurem on selle vaadeldav väärtus Kobs, seda tugevam on argument põhihüpoteesi vastu.

Seetõttu on selle statistika jaoks kriitiline piirkond alati paremakäeline :)