Kuidas lahendada ebavõrdsust kahe muutujaga. Kahe muutujaga võrrandid ja nende geomeetriline lahendus
Tihti on vaja koordinaattasandil kujutada kahe muutujaga võrratuse lahendite komplekti. Kahe muutuja ebavõrdsuse lahendus on nende muutujate väärtuste paar, mis muudab ebavõrdsuse tõeliseks numbriliseks ebavõrdsuseks.
2у+ Zx< 6.
Esiteks konstrueerime sirge. Selleks kirjutame võrratuse võrrandi kujul 2у+ Zx = 6 ja väljendada y. Seega saame: y=(6-3x)/2.
See joon jagab koordinaattasandi kõigi punktide hulga selle kohal asuvateks punktideks ja selle all asuvateks punktideks.
Võtke igast piirkonnast meem kontrollpunkt näiteks A (1;1) ja B (1;3)
Punkti A koordinaadid rahuldavad seda võrratust 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.
Punkti B koordinaadid Mitte rahulda see ebavõrdsus 2∙3 + 3∙1< 6.
Kuna see võrratus võib muuta märki sirgel 2y + 3x = 6, siis on ebavõrdsus rahuldatud punktide hulgaga piirkonnas, kus punkt A asub.
Seega oleme kujutanud ebavõrdsuse lahenduste komplekti 2a + 3x< 6.
Näide
Kujutame koordinaattasandil võrratuse x 2 + 2x + y 2 - 4y + 1 > 0 lahendite hulka.
Koostame esmalt graafiku võrrandist x 2 + 2x + y 2 - 4y + 1 = 0. Eraldame selles võrrandis oleva ringi võrrandi: (x 2 + 2x + 1) + (y 2 - 4y + 4) = 4 või (x + 1) 2 + (y - 2) 2 = 2 2 .
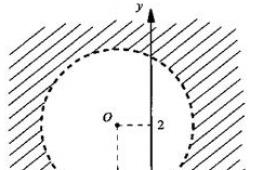
See on võrrand ringist, mille keskpunkt on punktis 0 (-1; 2) ja raadius R = 2. Ehitame selle ringi.

Kuna see võrratus on range ja ringil endal asuvad punktid ebavõrdsust ei rahulda, konstrueerime ringi punktiirjoonega.
Lihtne on kontrollida, et ringi keskpunkti O koordinaadid seda ebavõrdsust ei rahulda. Avaldis x 2 + 2x + y 2 - 4y + 1 muudab konstrueeritud ringil oma märki. Siis on ebavõrdsus rahuldatud punktidega, mis asuvad väljaspool ringi. Need punktid on varjutatud.
Näide
Kujutagem koordinaattasandil võrratuse lahendite hulka
(y - x 2) (y - x - 3)< 0.
Kõigepealt koostame võrrandi (y - x 2)(y - x - 3) = 0 graafiku. See on parabool y = x 2 ja sirge y = x + 3. Koostame need jooned ja paneme tähele, et avaldise (y - x 2)(y - x - 3) märgi muutus toimub ainult neil ridadel. Punkti A (0; 5) jaoks määrame selle avaldise märgi: (5-3) > 0 (st see võrratus ei kehti). Nüüd on lihtne märkida punktide kogum, mille puhul see ebavõrdsus on rahuldatud (need alad on varjutatud).

Kahe muutujaga võrratuste lahendamise algoritm
1. Taandame ebavõrdsuse kujule f (x; y)< 0 (f (х; у) >0; f (x; y) ≤ 0; f (x; y) ≥ 0;)
2. Kirjutage võrdus f (x; y) = 0
3. Tuvasta vasakule poole kirjutatud graafikud.
4. Koostame need graafikud. Kui ebavõrdsus on range (f (x; y)< 0 или f (х; у) >0), siis - kriipsudega, kui ebavõrdsus ei ole range (f (x; y) ≤ 0 või f (x; y) ≥ 0), siis - pideva joonega.
5. Määrake, mitmeks graafika osaks koordinaattasand on jagatud
6. Valige ühest neist osadest kontrollpunkt. Määrake avaldise f (x; y) märk
7. Asetame märgid teistesse tasapinna osadesse, võttes arvesse vaheldumist (nagu intervallmeetodil)
8. Valime välja meile vajalikud osad vastavalt lahendatava ebavõrdsuse märgile ja rakendame varjutuse
Teema: Võrrandid ja võrratused. Võrrandi- ja võrratussüsteemid
Õppetund:Kahe muutujaga võrrandid ja võrratused
Vaatleme üldiselt kahe muutujaga võrrandit ja võrratust.
Võrrand kahe muutujaga;
Kahe muutujaga ebavõrdsus, ebavõrdsuse märk võib olla ükskõik milline;
Siin on x ja y muutujad, p on neist sõltuv avaldis
Arvupaari () nimetatakse sellise võrrandi või võrratuse osaliseks lahendiks, kui selle paari avaldisesse asendamisel saame vastavalt õige võrrandi või võrratuse.
Ülesanne on leida või kujutada tasapinnal kõigi lahenduste hulk. Saate seda ülesannet ümber sõnastada – leida punktide asukoht (GLP), koostada võrrandi või võrratuse graafik.
Näide 1 - lahendage võrrand ja ebavõrdsus:
Teisisõnu, ülesanne hõlmab GMT leidmist.
Vaatleme võrrandi lahendust. Sel juhul võib muutuja x väärtus olla mis tahes, seega on meil:
Ilmselt on võrrandi lahenduseks sirge moodustavate punktide hulk

Riis. 1. Võrrandigraafik Näide 1
Antud võrrandi lahendid on eelkõige punktid (-1; 0), (0; 1), (x 0, x 0 +1)
Antud võrratuse lahendiks on sirge kohal paiknev pooltasand, sealhulgas sirge ise (vt joonis 1). Tõepoolest, kui me võtame sirgel suvalise punkti x 0, siis on meil võrdsus . Kui me võtame punkti pooltasapinnal joone kohal, on meil . Kui võtame joone all oleva pooltasandi punkti, siis see ei rahulda meie ebavõrdsust: .
Nüüd kaaluge probleemi ringi ja ringiga.
Näide 2 - lahendage võrrand ja ebavõrdsus:
Teame, et antud võrrand on ringi võrrand, mille keskpunkt on lähtepunktis ja raadius 1.

Riis. 2. Illustratsioon näiteks 2
Suvalises punktis x 0 on võrrandil kaks lahendit: (x 0; y 0) ja (x 0; -y 0).
Antud ebavõrdsuse lahendus on ringi sees paiknevate punktide kogum, mis ei võta arvesse ringi ennast (vt joonis 2).
Vaatleme võrrandit moodulitega.
Näide 3 – lahendage võrrand:
Sel juhul oleks võimalik mooduleid laiendada, kuid arvestame võrrandi eripäradega. On lihtne näha, et selle võrrandi graafik on sümmeetriline mõlema telje suhtes. Siis kui punkt (x 0 ; y 0) on lahend, siis on ka punkt (x 0 ; -y 0) lahendus, punktid (-x 0 ; y 0) ja (-x 0 ; -y 0) ) on samuti lahendus.
Seega piisab, kui leida lahendus, kus mõlemad muutujad on mittenegatiivsed ja võtavad telgede suhtes sümmeetriat:

Riis. 3. Illustratsioon näiteks 3
Niisiis, nagu näeme, on võrrandi lahendus ruut.
Vaatame nn pindalameetodit konkreetse näite varal.
Näide 4 - kujutage ebavõrdsuse lahenduste komplekti:
Domeenide meetodi järgi vaatleme kõigepealt vasakpoolset funktsiooni, kui paremal on null. See on kahe muutuja funktsioon:
![]()
Sarnaselt intervallide meetodile eemaldume ajutiselt ebavõrdsusest ja uurime koostatud funktsiooni tunnuseid ja omadusi.
ODZ: see tähendab, et x-telg torgatakse.
Nüüd näitame, et funktsioon on võrdne nulliga, kui murdosa lugeja on võrdne nulliga, on meil:
Koostame funktsiooni graafiku.

Riis. 4. Funktsiooni graafik, võttes arvesse ODZ-d
Vaatleme nüüd funktsiooni konstantse märgi alasid, mille moodustavad sirgjoon ja katkendjoon. katkendjoone sees on ala D 1. Katkendjoone ja sirge lõigu vahel - ala D 2, joone all - ala D 3, katkendjoone ja sirge segmendi vahel - ala D 4
Igas valitud piirkonnas säilitab funktsioon oma märgi, mis tähendab, et piisab suvalise katsepunkti kontrollimisest igas piirkonnas.
Piirkonnas võtame punkti (0;1). Meil on:
![]()
Piirkonnas võtame punkti (10;1). Meil on:
![]()
Seega on kogu piirkond negatiivne ega rahulda antud ebavõrdsust.
Piirkonnas võtke punkt (0;-5). Meil on:
![]()
Seega on kogu regioon positiivne ja rahuldab antud ebavõrdsust.
Kahe muutuja võrratuse lahendamine, ja veelgi enam kahe muutujaga võrratuste süsteemid, tundub üsna raske ülesanne olevat. Siiski on olemas lihtne algoritm, mis aitab sedalaadi pealtnäha väga keerukaid probleeme lihtsalt ja ilma suurema vaevata lahendada. Proovime selle välja mõelda.
Olgu meil ebavõrdsus kahe muutujaga, mis on ühte järgmistest tüüpidest:
y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).
Sellise ebavõrdsuse lahenduste hulga kujutamiseks koordinaattasandil toimige järgmiselt.
1. Koostame funktsiooni y = f(x) graafiku, mis jagab tasandi kaheks piirkonnaks.
2. Valime saadud aladest suvalise ja arvestame selles suvalise punktiga. Kontrollime selle punkti algse ebavõrdsuse teostatavust. Kui testi tulemuseks on õige arvuline võrratus, siis järeldame, et algne võrratus on täidetud kogu piirkonnas, kuhu valitud punkt kuulub. Seega on ebavõrdsuse lahenduste hulk piirkond, kuhu valitud punkt kuulub. Kui kontrolli tulemuseks on vale numbriline võrratus, siis on võrratuse lahendite hulk teine piirkond, kuhu valitud punkt ei kuulu.
3.
Kui ebavõrdsus on range, siis piirkonna piirid ehk funktsiooni y = f(x) graafiku punktid ei kuulu lahenduste hulka ja piir on kujutatud punktiirjoonega. Kui ebavõrdsus ei ole range, kaasatakse piirkonna piirid, see tähendab funktsiooni y = f(x) graafiku punktid selle võrratuse lahenduste hulka ja see piir on sel juhul kujutatud. pideva joonena.
Vaatame nüüd mitmeid selle teemaga seotud probleeme.
Ülesanne 1.
Millise punktide hulga annab võrratus x · y ≤ 4?
Lahendus.
1) Koostame graafiku võrrandist x · y = 4. Selleks teisendame selle esmalt. Ilmselgelt ei muutu x sel juhul 0-ks, sest vastasel juhul oleks meil 0 · y = 4, mis on vale. See tähendab, et saame oma võrrandi jagada x-ga. Saame: y = 4/x. Selle funktsiooni graafik on hüperbool. See jagab kogu tasapinna kaheks piirkonnaks: hüperbooli kahe haru vahele jäävasse ja neist väljapoole jäävasse piirkonda.
2) Valime esimesest piirkonnast suvalise punkti, olgu selleks punkt (4; 2).
Kontrollime ebavõrdsust: 4 · 2 ≤ 4 – väär.
See tähendab, et selle piirkonna punktid ei rahulda algset ebavõrdsust. Siis võime järeldada, et ebavõrdsuse lahenduste hulk on teine piirkond, kuhu valitud punkt ei kuulu.
3) Kuna ebavõrdsus ei ole range, siis tõmbame piiripunktid ehk funktsiooni y = 4/x graafiku punktid pideva joonega.
Värvime kollaseks punktide komplekti, mis määratleb algse ebavõrdsuse (joonis 1).
2. ülesanne.
Joonistage süsteemi poolt koordinaattasandile määratud ala
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.
Lahendus.
Alustuseks koostame järgmiste funktsioonide graafikud (Joonis 2):
y = x 2 + 2 – parabool,
y + x = 1 – sirgjoon
x 2 + y 2 = 9 – ring.

1) y > x 2 + 2.
Võtame punkti (0; 5), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 5 > 0 2 + 2 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad antud parabooli kohal y = x 2 + 2, süsteemi esimest võrratust. Värvime need kollaseks.
2) y + x > 1.
Võtame punkti (0; 3), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 3 + 0 > 1 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad sirge y + x = 1 kohal, süsteemi teist võrratust. Värvime need rohelise varjundiga.
3) x 2 + y 2 ≤ 9.
Võtke punkt (0; -4), mis asub väljaspool ringi x 2 + y 2 = 9.
Kontrollime ebavõrdsust: 0 2 + (-4) 2 ≤ 9 – vale.
Seetõttu on kõik punktid, mis asuvad väljaspool ringi x 2 + y 2 = 9,  ei rahulda süsteemi kolmandat ebavõrdsust. Siis võime järeldada, et kõik punktid, mis asuvad ringi sees x 2 + y 2 = 9, rahuldavad süsteemi kolmandat võrratust. Värvime need lilla varjundiga.
ei rahulda süsteemi kolmandat ebavõrdsust. Siis võime järeldada, et kõik punktid, mis asuvad ringi sees x 2 + y 2 = 9, rahuldavad süsteemi kolmandat võrratust. Värvime need lilla varjundiga.
Ärge unustage, et kui ebavõrdsus on range, tuleks vastav piirijoon tõmmata punktiirjoonega. Saame järgmise pildi (Joonis 3).

(Joonis 4).
3. ülesanne.
Joonistage süsteemiga koordinaattasandile määratud ala:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.
Lahendus.
Alustuseks koostame järgmiste funktsioonide graafikud: 
x 2 + y 2 = 16 – ring,
x = -y – sirgjoon
x 2 + y 2 = 4 – ring (Joonis 5).
Vaatame nüüd iga ebavõrdsust eraldi.
1) x 2 + y 2 ≤ 16.
Võtke punkt (0; 0), mis asub ringi sees x 2 + y 2 = 16.
Kontrollime ebavõrdsust: 0 2 + (0) 2 ≤ 16 – tõene.
Seetõttu rahuldavad kõik punktid, mis asuvad ringi sees x 2 + y 2 = 16, süsteemi esimest võrratust.
Värvime need punase varjundiga. 
Võtame punkti (1; 1), mis asub funktsiooni graafiku kohal.
Kontrollime ebavõrdsust: 1 ≥ -1 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad sirge x = -y kohal, süsteemi teist võrratust. Värvime need sinise varjundiga.
3) x 2 + y 2 ≥ 4.
Võtke punkt (0; 5), mis asub väljaspool ringi x 2 + y 2 = 4.
Kontrollime ebavõrdsust: 0 2 + 5 2 ≥ 4 – tõene.
Järelikult rahuldavad kõik punktid, mis asuvad väljaspool ringi x 2 + y 2 = 4, süsteemi kolmandat võrratust. Värvime need siniseks.
Selles ülesandes ei ole kõik ebavõrdsused ranged, mis tähendab, et me tõmbame kõik piirid pideva joonega. Saame järgmise pildi (Joonis 6).
Otsinguala on ala, kus kõik kolm värvilist ala ristuvad üksteisega (Joonis 7).

Kas teil on endiselt küsimusi? Ei tea, kuidas lahendada kahe muutujaga võrratuste süsteemi?
Juhendajalt abi saamiseks -.
Esimene tund on tasuta!
blog.site, materjali täielikul või osalisel kopeerimisel on vaja linki algallikale.
Videotund “Ebavõrdsused kahe muutujaga” on mõeldud selleteemaliseks algebra õpetamiseks keskkooli 9. klassis. Videotund sisaldab ebavõrdsuse lahendamise teoreetiliste aluste kirjeldust, kirjeldab üksikasjalikult graafiliselt ebavõrdsuse lahendamise protsessi, selle tunnuseid ning demonstreerib näiteid teemakohaste ülesannete lahendamisest. Selle videotunni eesmärk on hõlbustada materjali mõistmist teabe visuaalse esituse abil, soodustada ülesannete lahendamise oskuste kujunemist õpitud matemaatilisi meetodeid kasutades.
Videotunni peamisteks töövahenditeks on animatsiooni kasutamine graafikute ja teoreetilise info esitamisel, materjali mõistmiseks ja meeldejätmiseks oluliste mõistete ja tunnuste esiletõstmine värvilisel ja muul graafilisel viisil, häälselgitused teabe kergema meeldejätmise eesmärgil ning matemaatilise keele kasutamise oskuse kujunemine.
Videotund algab teema tutvustamisega ja näitega, mis demonstreerib ebavõrdsuse lahendamise kontseptsiooni. Lahenduse mõiste tähenduse mõistmiseks esitatakse võrratus 3x 2 -y<10, в которое подставляется пара значений х=2 и у=6. Демонстрируется, как после подстановки данных значений неравенство становится верным. Понятие решения данного неравенства как пары значений (2;6) выведено на экран, подчеркивая его важность. Затем представляется определение рассмотренного понятия для запоминания его учениками или записи в тетрадь.
Võrratuste lahendamise oskuse oluline osa on oskus kujutada selle lahendite hulka koordinaattasandil. Sellise oskuse kujundamine selles tunnis algab lineaarsete ebavõrdsuste ax+by lahenduste leidmise demonstreerimisega.

Sellise ebavõrdsuse näide on x+3y>6. Võrratuse teisendamiseks samaväärseks võrratuseks, mis peegeldab y väärtuste sõltuvust x väärtustest, jagatakse võrratuse mõlemad pooled 3-ga, y jääb võrrandi ühele küljele ja x kantakse üle teine. Väärtus x=3 valitakse meelevaldselt ebavõrdsusega asendamiseks. Tuleb märkida, et kui asendada see x väärtus ebavõrdsusega ja asendada ebavõrdsusmärk võrdusmärgiga, leiate vastava väärtuse y=1. Paar (3;1) on võrrandi y=-(1/3)x+2 lahendus. Kui asendame y väärtused, mis on suuremad kui 1, on ebavõrdsus antud väärtusega x tõene: (3;2), (3;8) jne. Sarnaselt sellele lahenduse leidmise protsessile on ka vaadeldakse antud ebavõrdsuse lahenduste leidmise üldist juhtumit. Ebavõrdsuse lahenduste komplekti otsimine algab teatud väärtuse x 0 asendamisega. Ebavõrdsuse paremal küljel saame avaldise -(1/3)x 0 +2. Teatud arvupaar (x 0;y 0) on võrrandi y=-(1/3)x+2 lahend. Sellest lähtuvalt on võrratuse y>-(1/3)x 0 +2 lahendid vastavad väärtuste paarid x 0-ga, kus y on suurem kui y 0 väärtused. See tähendab, et selle ebavõrdsuse lahendused on väärtuste paarid (x 0 ; y).
Võrratuse x+3y>6 lahendite hulga leidmiseks koordinaattasandil demonstreeritakse sellel võrrandile y=-(1/3)x+2 vastava sirge konstrueerimist. Sellel sirgel on punkt M tähistatud koordinaatidega (x 0; y 0). Tuleb märkida, et kõik punktid K(x 0;y), mille ordinaadid on y>y 0, st mis asuvad sellest sirgest kõrgemal, vastavad ebavõrdsuse y>-(1/3)x+2 tingimustele. Analüüsist järeldatakse, et selle võrratuse annab punktide hulk, mis asuvad sirge y=-(1/3)x+2 kohal. See punktide komplekt moodustab antud sirge pooltasandi. Kuna ebavõrdsus on range, siis sirgjoont ennast lahenduste hulgas ei ole. Joonisel on see asjaolu tähistatud punktiirjoonega.
Võttes kokku võrratuse x+3y>6 lahendi kirjeldamise tulemusena saadud andmed, võib öelda, et sirge x+3y=6 jagab tasapinna kaheks pooltasandiks, ülal paiknev pooltasapind aga peegeldab väärtuste kogum, mis rahuldab võrratust x+3y>6 ja asub joone all - võrratuse x+3y lahendus<6. Данный вывод является важным для понимания, каким образом решаются неравенства, поэтому выведен на экран отдельно в рамке.

Järgmisena vaatleme näidet teise astme y>=(x-3) 2 mitterange ebavõrdsuse lahendamisest. Lahenduste hulga määramiseks konstrueeritakse joonisel lähedale parabool y = (x-3) 2. Paraboolile on märgitud punkt M(x 0 ; y 0), mille väärtused on võrrandi y = (x-3) 2 lahendid. Siinkohal konstrueeritakse risti, millele parabooli kohale on märgitud punkt K(x 0 ;y), mis on võrratuse y>(x-3) 2 lahend. Võime järeldada, et algne võrratus on rahuldatud punktide koordinaatidega, mis asuvad antud paraboolil y = (x-3) 2 ja sellest kõrgemal. Joonisel on see lahendusala tähistatud varjutusega.

Järgmine näide, mis demonstreerib teise astme võrratuse lahendiks olevate punktide asukohta tasapinnal, on võrratuse x 2 + y 2 lahendi kirjeldus.<=9. На координатной плоскости строится окружность радиусом 3 с центром в начале координат. Отмечается, что решениями уравнения будут точки, сумма квадратов координат которых не превышает квадрата радиуса. Также отмечается, что окружность х 2 +у 2 =9 разбивает плоскость на области внутри окружности и вне круга. Очевидно, что множество точек внутренней части круга удовлетворяют неравенству х 2 +у 2 <9, а внешняя часть - неравенству х 2 +у 2 >9. Vastavalt sellele on esialgse ebavõrdsuse lahenduseks ringi punktide kogum ja selle sees olev piirkond.
Järgmisena vaatleme võrrandi xy>8 lahendust. Ülesande kõrval asuvale koordinaattasandile konstrueeritakse hüperbool, mis rahuldab võrrandit xy=8. Märgi y-teljega paralleelselt hüperboolile kuuluv punkt M(x 0;y 0) ja selle kohal K(x 0;y). On ilmne, et punkti K koordinaadid vastavad ebavõrdsusele xy>8, kuna selle punkti koordinaatide korrutis ületab 8. Juhime tähelepanu, et samamoodi saab tõestada piirkonda B kuuluvate punktide vastavust alale B. ebavõrdsus xy<8. Следовательно, решением неравенства ху>8 on punktide komplekt, mis asub aladel A ja C.
Videotund “Ebavõrdsused kahe muutujaga” võib olla õpetajale klassiruumis visuaalseks abivahendiks. Materjal on abiks ka õpilastele, kes õpivad materjali iseseisvalt. Kaugõppes on kasulik kasutada videotundi.