Funktsiooni k x graafik. Lineaarne funktsioon

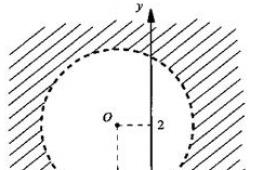
Vaatleme funktsiooni y=k/y. Selle funktsiooni graafik on sirge, mida matemaatikas nimetatakse hüperbooliks. Hüperbooli üldvaade on näidatud alloleval joonisel. (Graafik näitab funktsiooni y võrdub k jagatuna x-ga, mille puhul k on üks.)

On näha, et graafik koosneb kahest osast. Neid osi nimetatakse hüperbooli harudeks. Samuti väärib märkimist, et iga hüperbooli haru läheneb ühes suunas, mis on koordinaatide telgedele lähemal. Koordinaatide telgi nimetatakse sel juhul asümptootideks.

Üldiselt nimetatakse asümptootideks kõiki sirgeid, millele funktsiooni graafik lõpmatult läheneb, kuid ei jõua nendeni. Hüperboolil, nagu paraboolil, on sümmeetriateljed. Ülaltoodud joonisel kujutatud hüperbooli jaoks on see sirge y=x.

Vaatame nüüd kahte levinud hüperbooli juhtumit. Funktsiooni y = k/x graafik k ≠0 korral on hüperbool, mille harud asuvad kas esimeses ja kolmandas koordinaatnurgas, kui k>0, või teises ja neljandas koordinaatnurgas, jaoks k<0.

Funktsiooni y = k/x põhiomadused, kui k>0

Funktsiooni y = k/x graafik, kui k>0

5. y>0 x>0 juures; y6. Funktsioon väheneb nii intervallil (-∞;0) kui ka intervallil (0;+∞).

10. Funktsiooni väärtuste vahemik on kaks avatud intervalli (-∞;0) ja (0;+∞).

Funktsiooni y = k/x põhiomadused k jaoks<0

Funktsiooni y = k/x graafik k juures<0

1. Punkt (0;0) on hüperbooli sümmeetriakese.

2. Koordinaatide teljed - hüperbooli asümptoodid.

4. Funktsiooni määratluspiirkond on kõik x, välja arvatud x=0.

5. y>0 x0 juures.

6. Funktsioon suureneb nii intervallil (-∞;0) kui ka intervallil (0;+∞).

7. Funktsioon ei ole piiratud ei alt ega ülevalt.

8. Funktsioonil ei ole ei maksimum- ega miinimumväärtust.

9. Funktsioon on pidev intervallil (-∞;0) ja intervallil (0;+∞). Kui x=0 on tühimik.

1. Kui muutuja y on võrdeline muutujaga x, siis seda sõltuvust väljendatakse valemiga kus on proportsionaalsustegur. Uurisime selle funktsiooni graafikut §-s 2.

2. Kui muutuja y on pöördvõrdeline muutujaga x, siis seda sõltuvust väljendatakse valemiga kus on pöördvõrdelisuse koefitsient.

3. Funktsiooni domeen on kõikide arvude hulk peale nulli, s.t.

4. Pöördproportsionaalsuse graafik on kõver, mis koosneb kahest harust, mis on sümmeetrilised alguspunkti suhtes. Sellist kõverat nimetatakse hüperbooliks (joonis 35). Kui siis hüperbooli harud paiknevad I ja III koordinaatveerandis; kui, siis II ja IV koordinaatveerandis.

5. Pange tähele, et hüperbool ei oma koordinaattelgedega ühiseid punkte, vaid läheneb neile ainult meelevaldselt lähedale (selgitage, miks).

HARJUTUSED LAHENDUStega

Joonistage funktsiooni graafik:

Lahendus. 1) Selle praktikas sageli esineva funktsiooni graafiku joonistamiseks määrame kõigepealt kindlaks selle mõned omadused.

a) Funktsioon on määratletud kõigi reaalväärtuste jaoks, kuna funktsioon pole määratletud (nulliga jagada ei saa!). Seega koosneb funktsiooni määratluspiirkond kahest intervallist:

b) Funktsioon on paaritu, kuna Järelikult on selle graafik sümmeetriline alguspunkti suhtes. Seetõttu piisab, kui kaaluda seda funktsiooni ainult

c) Kui funktsioon väheneb. Tõepoolest, las siis

Funktsioon on kujutatud joonisel 35. Seda kõverat nimetatakse hüperbooliks. See koosneb kahest harust, mis asuvad I ja III koordinaatkvartalis.

Funktsiooni Koefitsient k võib võtta mis tahes väärtuse, välja arvatud k = 0. Vaatleme esmalt juhtumit, kui k = 1; seega räägime kõigepealt funktsioonist.

Funktsiooni graafiku koostamiseks teeme sama, mis eelmises lõigus: anname sõltumatule muutujale x mitu konkreetset väärtust ja arvutame (valemi abil) sõltuva muutuja vastavad väärtused. muutuv u. Tõsi, seekord on mugavam teha arvutusi ja konstruktsioone järk-järgult, andes argumendile esmalt ainult positiivsed väärtused ja seejärel ainult negatiivsed.

Esimene etapp. Kui x = 1, siis y = 1 (tuletame meelde, et kasutame valemit);

Teine etapp.

Lühidalt, oleme koostanud järgmise tabeli:

Nüüd ühendame kaks etappi üheks, st teeme kahest joonisest 24 ja 26 ühe (joonis 27). See on see funktsiooni graafik seda nimetatakse hüperbooliks.
Proovime joonise abil kirjeldada hüperbooli geomeetrilisi omadusi.

Esiteks, märkame, et see joon näeb välja sama ilus kui parabool, kuna sellel on sümmeetria. Iga koordinaatide O alguspunkti läbiv sirge, mis asub esimeses ja kolmandas koordinaatnurgas, lõikab hüperbooli kahes punktis, mis asuvad sellel sirgel punkti O vastaskülgedel, kuid sellest võrdsel kaugusel (joonis 28). See on omane eelkõige punktidele (1; 1) ja (- 1; - 1),

Jne See tähendab – O on hüperbooli sümmeetriakese. Nad ütlevad ka, et hüperbool on päritolu suhtes sümmeetriline koordinaadid.

Teiseks, näeme, et hüperbool koosneb kahest osast, mis on alguspunkti suhtes sümmeetrilised; neid nimetatakse tavaliselt hüperbooli harudeks.

Kolmandaks märkame, et hüperbooli iga haru ühes suunas läheneb abstsissteljele ja teises suunas ordinaatteljele. Sellistel juhtudel nimetatakse vastavaid sirgeid asümptootideks.

See tähendab, et funktsiooni graafik, s.o. hüperboolil on kaks asümptooti: x-telg ja y-telg.

Kui analüüsite joonistatud graafikut hoolikalt, võite avastada veel ühe geomeetrilise omaduse, mis pole nii ilmne kui kolm eelmist (matemaatikud ütlevad tavaliselt seda: "peenem omadus"). Hüperboolil pole mitte ainult sümmeetriakese, vaid ka sümmeetriateljed.

Tegelikult konstrueerime sirge y = x (joonis 29). Nüüd vaadake: punktid asub vastaskülgedel läbiviidud otsene, kuid sellest võrdsel kaugusel. Need on selle sirgjoone suhtes sümmeetrilised. Sama võib öelda ka punktide kohta, kus see muidugi tähendab, et sirge y = x on hüperbooli sümmeetriatelg (nagu ka y = -x)

Näide 1. Leia funktsiooni a) väikseim ja suurim väärtus lõigul ; b) lõigul [- 8, - 1].
Lahendus, a) Koostame funktsiooni graafiku ja valime segmendist selle osa, mis vastab muutuja x väärtustele (joonis 30). Graafiku valitud osa kohta leiame:

b) Koostage funktsiooni graafik ja valige sellest see osa, mis vastab muutuja x väärtustele. segment[- 8, - 1] (joonis 31). Graafiku valitud osa kohta leiame:

Seega oleme vaadelnud funktsiooni juhul, kui k = 1. Olgu k nüüd 1-st erinev positiivne arv, näiteks k = 2.

Vaatleme funktsiooni ja koostame selle funktsiooni väärtuste tabeli:

Koostame punktid (1; 2), (2; 1), (-1; -2), (-2; -1),

koordinaattasandil (joonis 32). Nad visandavad teatud joone, mis koosneb kahest harust; Teeme selle läbi (joonis 33). Nagu funktsiooni graafikut, nimetatakse seda sirget hüperbooliks.

Vaatleme nüüd juhtumit, kui k< 0; пусть, например, k = - 1. Построим график функции (здесь k = - 1).

Eelmises lõigus märkisime, et funktsiooni y = -f(x) graafik on sümmeetriline funktsiooni y = f(x) graafiku suhtes x-telje ümber. Eelkõige tähendab see, et funktsiooni y = - f(x) graafik on sümmeetriline funktsiooni y = f(x) graafiku suhtes x-telje suhtes. Eelkõige tähendab see seda ajakava, on graafiku suhtes sümmeetriline x-telje suhtes (joonis 34) Nii saame hüperbooli, mille harud paiknevad teises ja neljandas koordinaatnurgas.

Üldiselt funktsiooni graafik on hüperbool, mille harud asuvad esimeses ja kolmandas koordinaatnurgas, kui k > 0 (joonis 33), ning teises ja neljandas koordinaatnurgas, kui k< О (рис. 34). Точка (0; 0) - центр симметрии гиперболы, оси координат - асимптоты гиперболы.

Tavaliselt öeldakse, et kaks suurust x ja y on pöördvõrdelised, kui need on seotud seosega xy = k (kus k on 0-st erinev arv), või, mis on sama, . Sel põhjusel nimetatakse funktsiooni mõnikord pöördproportsionaalsuseks (analoogiliselt funktsiooniga y - kx, mis, nagu te ilmselt teate,
pidage meeles, et seda nimetatakse otseseks proportsionaalsuseks); arv k - pöördkoefitsient proportsionaalsus.

Funktsiooni omadused k > 0 korral

Selle funktsiooni omadusi kirjeldades toetume selle geomeetrilisele mudelile – hüperboolile (vt joonis 33).

2. y > 0, kui x>0;y<0 при х<0.

3. Funktsioon väheneb intervallidel (-°°, 0) ja (0, +°°).

5. Mitte funktsiooni väikseimad ega suurimad väärtused

Funktsiooni omadused k< 0
Kirjeldades selle funktsiooni omadusi, tugineme selle geomeetriale mudel- hüperbool (vt joonis 34).

1. Funktsiooni domeen koosneb kõigist arvudest peale x = 0.

2. y > 0 x juures< 0; у < 0 при х > 0.

3. Funktsioon suureneb intervallidel (-oo, 0) ja (0, +oo).

4. Funktsioon ei ole piiratud ei alt ega ülevalt.

5. Funktsioonil pole ei väikseimaid ega suurimaid väärtusi.

6. Funktsioon on pidev intervallidel (-oo, 0) ja (0, +oo) ning läbib katkestuse, kui x = 0.

Tunni sisu tunnimärkmed toetavad raamtunni esitluskiirendusmeetodid interaktiivseid tehnoloogiaid Harjuta ülesanded ja harjutused enesetesti töötoad, koolitused, juhtumid, ülesanded kodutöö arutelu küsimused retoorilised küsimused õpilastelt Illustratsioonid heli, videoklipid ja multimeedium fotod, pildid, graafika, tabelid, diagrammid, huumor, anekdoodid, naljad, koomiksid, tähendamissõnad, ütlused, ristsõnad, tsitaadid Lisandmoodulid kokkuvõtteid artiklid nipid uudishimulikele hällid õpikud põhi- ja lisaterminite sõnastik muu Õpikute ja tundide täiustaminevigade parandamine õpikusõpiku fragmendi uuendamine, innovatsioonielemendid tunnis, vananenud teadmiste asendamine uutega Ainult õpetajatele täiuslikud õppetunnid aasta kalenderplaan; Integreeritud õppetunnid

Esitluse eelvaadete kasutamiseks looge Google'i konto ja logige sisse: https://accounts.google.com

Slaidi pealdised:

Funktsioon y=k/x, selle omadused ja graafik. MKOU "Hokholski lütseumi" matemaatikaõpetaja Logvinova Irina Alekseevna

Hariduslik: sõnastada pöördproportsionaalsuse definitsioon, selle definitsiooni ulatus; õpetada koostama funktsiooni y = k / x graafikut, lähtudes funktsiooni omadustest; luua selge ettekujutus funktsioonigraafiku omaduste ja asukoha erinevustest k erinevate väärtuste korral; õpetada, kuidas leida funktsiooni ja argumendi väärtust valemiga Y = k/x. Arendav: parandab loogilise mõtlemise ja oma mõtete valjuhäälse väljendamise võimet; stimuleerida õpilaste tunnetuslikku tegevust probleemülesande püstitamise, hindamise ja julgustamise kaudu; edendada leidlikkuse ja intelligentsuse arengut. Haridus: sisendada õpilastesse soov oma teadmisi täiendada; teema vastu huvi kasvatada. 2 Tunni eesmärgid

07.10.2014 3 Funktsioonide tüübid Ühe muutuja sõltuvust teisest nimetatakse funktsiooniks y = kx y=x 3 y=x 2 y = kx+b

07.10.2014 4 Jalgratturi kiirus V km/h; t h – aeg. Kui kaua kulub jalgratturil 20 km läbimiseks? Väljendage t sõltuvust V-st.

07.10.2014 5 Ristküliku pindala on 35 ruutmeetrit. cm Ristküliku üks külg on cm, teine ​​on cm. Avaldage a sõltuvust.

07.10.2014 6 R hõõruda. kauba hind, m kauba kogus. Mitu kaupa saab osta 90 rubla eest? Väljendage m sõltuvust P-st.

07.10.2014 7 Mis on neil valemitel ühist ja millised on erinevused? Koostage funktsioon, mis on vaadeldavate sõltuvuste üldistus.

Definitsioon Pöördproportsionaalsus on funktsioon, mis on defineeritud valemiga y = k/x, kus k ≠ 0, kus x on sõltumatu muutuja. Arvu k nimetatakse pöördproportsionaalsuse kordajaks

Loodusnähtustes ja inimtegevuses kohtab sageli kahe suuruse vahelisi pöördvõrdelisi seoseid. Kuidas seda suhet graafikustada? Pöördvõrdelise funktsiooni graafikut nimetatakse HÜPERBOOLIKS

Funktsiooni 12 x _ y = x y -1 -2 -4 -3 -6 -8 -12 -12 -6 -4 -3 -2 -1,5 -1 x y 1 2 3 4 6 8 12 12 6 4 3 graafik 2 1.5 1 Koostame funktsiooni graafiku punktide kaupa

hüperbool

Valik 1 Variant 2 Funktsiooni y = k/x graafik ja selle omadused y = k/x, k˂0 y = k/x, k˃0 1. Funktsiooni domeen 2. Funktsiooni 3. y > domeen 0, a

14 Mõiste “funktsioon” 1664. aastal tutvustas saksa teadlane Leibniz. Funktsiooni määratluse andis tema õpilane Bernoulli aastal 1718. Üks esimesi, kes seda kõverat uurima hakkas, oli kuulsa Platoni õpilane, Vana-Kreeka matemaatik Menaechmus 4. sajandil. eKr, kuid kunagi ei õnnestunud seda täielikult uurida. Kuid ta uuris täielikult hüperbooli omadusi ja andis sellele nime antiikaja suurimale geomeetrile, Apolloniusele Pergast 3. sajandil. eKr

Testiülesanded teemal “Pöördproportsionaalsus” 1) Milline valemitest määrab pöördproportsionaalsuse 3) 4) 5) 1) 2)

2) Milline näidatud punktidest kuulub funktsiooni y = -8/x graafikusse? 1) A(1;8) 2) B(-1;-8) 3) C(1; -8) Testiülesanded teemal “Pöördproportsionaalsus”

1. Ühel pildil on hüperbool. Palun märkige see joonis. 1 3 4 2

Mis on funktsiooni graafik, millistes koordinaatveerandites asub funktsiooni graafik? Mis on funktsiooni määratluspiirkond. Millised omadused on pöördvõrdelise funktsiooni graafikul? Kuidas nimetatakse pöördvõrdelise funktsiooni graafikut? Millest koosneb hüperbool? 18 Tunni kokkuvõte

Huvitavad faktid 19 Ožegovi vene keele sõnaraamatust tähendab sõna hüperbool poeetikas – liigse liialdamise tehnikat mulje tugevdamiseks. Suures Vene entsüklopeedias (7. köide) - objekti või nähtuse kujutise teatud omaduste ebausutav liialdus. Näiteks: “...haruldane lind lendab keset Dneprit” N.V. Gogol. Hüperbooli leidub tihtipeale: laisk istub väravas, suu pärani, ja keegi ei tea, kus on värav ja kus on suu.